1.1 Mathematical description transm. lines: dimensions and el. properties are identical Uniform all planes transverse to the direction of propagation.
|
|
|
- Cipriana Stancu
- 4 ani în urmă
- Vzualizari:
Transcriere
1 1.1 Mathematical description transm. lines: dimensions and el. properties are identical Uniform all planes transverse to the direction of propagation. at of the transm. line need not be negligible compared Length the wavelength. Extension of a.c. circuit theory to DIS- to TRIBUTED circuits. resistance inductance capacitance Dene conductance and per G ; L ; C for uniform transm. line. ; R length: unit Explain dierence between R and G Microwave Circuit Design I cb. Pejcinovic 1
2 related to dimensions and conductivity of (metallic) conductors R G related to loss tangent of the insulating material between L related to magnetic ux linking the conductors C related to charge on conductors Fig. 3-1 (analogy to twin lead or coax) represents a \small" section of the transm. line small is z to the wavelength relative Microwave Circuit Design I cb. Pejcinovic 2
3 Kircho's laws for V and I for a small segment (sketch) z)i + (L V (R + (V + V ) (1) I = (I + I) + (V + V )(G z) + (C + V ) division by z gives: V (V + V ) z I (I + I) z I + = = (V + V )G + + V Microwave Circuit Design I cb. Pejcinovic (2) (3) (4)
4 Taking the limit z! = R I and = V G @z Analogous to the eqs. we had for E and H. Combining produces: V V C 2 + (R C + G L L + R G V 2 and similar for I. For perfect conductor R = perfect insulator G = Microwave Circuit Design I cb. Pejcinovic 4 (5)
5 = V C 2 and 2 = I 2 are wave eqs and their solutions are \EM wave"-like These along both directions. Both current and voltage waves. traveling In general solutions will satisfy f (t p L C z). at (z ) f (t) = V and at another z = z 1 where Look f = = p p L C z 1 ). By the time t = L C z 1 the value inside (t f = V is same as for z = ) only dierence is time delay of p () the C z. 1 L Microwave Circuit Design I cb. Pejcinovic 5
6 The velocity of propagation of such wave is = 1 v = z d t Note that f (t + 1 z p L 1 z C = 1 p C (8) L p C travels in negative direction. z) L I and V travel with the same velocity. EM waves we found that E/H was constant: same here but for of we have instead CHARACTERISTIC IMPEDANCE Z = V I = Microwave Circuit Design I cb. Pejcinovic 6 v uuu L u ut C (9)
7 1.2 Transient behavior Charging of an innite transmission line. (g. 3-2) of sequential current increases capacitance charging current Idea etc. Instantaneous changes impossible due to L and C. increase V and I generate each other and travel with the same velocity v. innite ) only + directed wave. Since V/I is constant only Line 1) is seen at all times. ) innite line presents Z load Z(= to the battery and it keeps drawing current. Note that the steady state at the input is reach immediately. Microwave Circuit Design I cb. Pejcinovic 7
8 Finite length: open circuit. Fig t = ;V = 1V appears at input of transm. line i.e. line At like and innite line ) input impedance = Z at t =. behaves current I in = V G =(R G + Z ) = 2=2 = :1A and input Input voltage V in = 1V. These stay constant until later (when reected wave arrives). propagation velocity v = m=s time it takes the wave For get to the end is t = l=v = 4=2 1 8 = 2ns. to 3-3 a) shows the situation at half the time it takes to travel Fig. the end and 3-3 b) is for time just before reaching the end. to Microwave Circuit Design I cb. Pejcinovic 8
9 Something must happen at the end of the line: constant ratio V + =I + = Z must be preserved for the traveling wave Z = 1 since the end is open-circuited. of traveling waves at O-C makes it possible to satisfy Reection requirements. both voltage and current at the load we have V L = V + + V and For L = I + I. Since I L = ) I + = I and V = I Z = I I + Z = V +. Finally V L = 2V + = 2V. reection coecient = V =V + = I =I + and is =1 for Dene case. O-C Microwave Circuit Design I cb. Pejcinovic 9
10 Current becomes zero as I wave returns and V goes to 2V. the generator end V =I = Z = 1 is the same as the At of the generator so no need for additional require- impedance ments to be satised ) no more reections. Resistive termination 3-4. part a) is as before. At the end of the line Z 6= R L Fig. Ohm's law is not satised if we also want to keep the Z and constant. Solution: reections must occur at load end. L = V + + V ; I L = I + I = (V + V )=Z. Ohm's law V L = I L R L ) V Microwave Circuit Design I cb. Pejcinovic 1
11 RL = V + + V + V 1 L or L = Z R L + Z = L 1 Z V In steady-state transm. line is a short circuit. Analogy with for TEM waves (= ( )=( + ). RL + Z (1) For resistance is real but it is complex for other terminations. = 1 for O-C and = 1 for S-C (short circuit). RL = Z no reections occur since Ohms law is automatically For satised. Microwave Circuit Design I cb. Pejcinovic 11
12 Multiple reections Both R L and R G 6= Z! see Fig t= generator sees Z (as before) ) I + = 9=3 = :3A At V + = 3V. R L has no inuence. and 2ns there is a reection on load end: L = (25 1)=125 After :6 resulting in V = V + = 18V. = voltage V total = V + + V = 12V. Similarly for reected Total total currents we have I = I + = :18A and Itot = IL = and :3 + :18 = :48A two combined waves reach source end and there is another These (R G 6= Z ): G = (R G Z )=(R G +Z ) = V refl =V inc = reection I refl =I inc = 1=3. Microwave Circuit Design I cb. Pejcinovic 12
13 To nd the reected part V ref = G V = 6V ; etc. the incident (incoming) wave is V = 18V which gives Now = 6V and new total voltage Vtot = 12 6 = 6V Vref reection at the load end this time the incident wave Another 6V so that V ref = 6 (:6) = 3:6V for the new V tot = is 6 + 3:6 = 9:6V. of reected waves get smaller with each reection Amplitudes (why?). d.c. value V = 9 R L =(R G + R L ) = 1V. Fig. 3-6 shows Final time evolution of the input voltage. the Microwave Circuit Design I cb. Pejcinovic 13
14 diagram: voltage and current as functions of time and Bewley's Fig Construct constant z diagram or nd value of position. V or I for xed t. xed z (=2m) intersections represent arrivals of wave fronts; For summed up; forward current waves added but reected voltages ones subtracted. t: sum of voltages at any z above the line gives V variation Fixed z (same for I) with occurs: period T=8ns (2 x round trip) or f = 1=T = Ringing For v = ) f = v and = 16m or l = =4. 12:5MHz. result: d.c. source produces high frequency oscillations. Interesting If both -s were unity ) continuous oscillations i.e. resonant circuit. Microwave Circuit Design I cb. Pejcinovic 14
15 1.3 Sinusoidal excitation Equations become (using phasor notation): d = (R + j!l ) ^I = Z ^I (11) ^V dz di = (G + j!c ) ^V = Y ^V (12) dz As for EM waves these are combined: 2 d = Z ^V ^V ) ^V = ^V + e z + ^V e z = V + + V (13) 2 Y dz As before is (complex) propagation constant. = p Y = Z s (R + j!l )(G + j!c ) = + j (14) Microwave Circuit Design I cb. Pejcinovic 15
16 For current we have: = ^I + e z ^I e +z = ^I + ^I (15) ^I impedance (voltage to current ratio fro traveling Characteristic waves) = V + Z I + V = I = v uuu Z u ut Y = v uuu u ut R + j!l G + j!c (16) and currents are phasor quantities and depend on conditions Voltages on load and generator end. Power ow : P = Re( ^V ^I ) = IV cos pf Example 3-1. Microwave Circuit Design I cb. Pejcinovic 16
17 Low-loss lines <<!L and G!C. Almost always At high frequency: R range. MW in true Z = v uuu L u ut R G Z ; + 2Z C! p L C v = Conclusions: 1 p L 2 Np/length (17) = p (18) C L c C Eqs. for Z ;v;; the same as for lossless lines. Microwave Circuit Design I cb. Pejcinovic 17
18 Since Z is practically real the average power ow in a traveling wave at any point z is product of rms voltage and current P + = V + I + and P = V I. frequency signals ) nite R ;G introduce attenuation For single waves (e z for power it's square). propagating on to EM waves in lossy dielectric. Reason: there is a wave Similar with sinusoidal waves but now it is guided. associated Microwave Circuit Design I cb. Pejcinovic 18
19 Coaxial transmission lines Fig. 3-8 shows E and H eld distribution. = V E ln b a r Average power ow: P = Z = I H 2r S ~ E ~ H d~s (19) (2) cylindrical coordinates: d~s = r d dr (d~s is element normal In the plane of paper i.e. cross-sectional area; sketch) to P = Z Z 2 b a I V 2 2r (why these limits?) ln b a 1 1 C A r ddr = V I (21) Microwave Circuit Design I cb. Pejcinovic 19
20 power ow associated with the voltage and current Interpretation: is just another way of viewing EM propagation in the region waves between conductors! From early on: C = 2 r l= ln(b=a). Divide by l to get C. Similarly L = r l ln(b=a)=(2). v = Z = 1 p C = L v uuu L u ut C = v uuu 1 = c p (familiar?) (22) p r r r r u t r 4 2 r ln b a = 6 v uuu u r t r ln b a Microwave Circuit Design I cb. Pejcinovic 2 (23)
21 1.4 Terminated transm. lines Discussion of various loads on transm. lines. view: tr. line terminated in its Z has no reections Alternative based on innite line picture. Conclusion: line terminated in Z is equivalent to innitely long line and has no reections. its impedance = Z. Input Fig. 3{9 ^Vin; ^Iin at point z=: ^Vin = Z ^ ^VG V G ^I = Z + ZG reections present ) ^V in = ^V + ; ^I in = ^I +. No ZG + Z (24) Microwave Circuit Design I cb. Pejcinovic 21
22 ^V ; ^I still vary along the line: = ^V + ez ^I = ^I + ez (25) ^V At the load end this gives (z=l): ^VL = Z ZG + Z ^VGe l 6 l ^IL = ^VG ZG + Z e l 6 l (26) the power absorbed by load? P L = V L I L (rms values) What's Z is real. since PL = Z V G ZG + Z 2 e 2l (27) magnitude needed since Z G may be complex Microwave Circuit Design I cb. Pejcinovic 22
23 General case (with reections) If Z L 6= Z ) reections. Starting point is = ^V + ez + ^V e+z = ^V + + ^V ^I = ^I + ez ^I e+z (28) ^V coe. was dened only at the load or generator end Reection no need for such a restriction ) dene it anywhere on line: (z) = V or I re. V or I = incident At load end we have: L = e l ^V + e l = ^V ^V ^I ^V = + ^V ^I + (29) + e 2l (3) ^V Microwave Circuit Design I cb. Pejcinovic 23
24 convenience: transform coordinated so that zero is at load For and + direction is towards generator (Fig. 3{1). New end coordinate: d=l-z. Voltage wave somewhere on the tr. line: + V el = ^V e d {z } 64 gen.!load L e d {z } + load!gen (31) ^I = ^I + e l " e l L e d# (32) Microwave Circuit Design I cb. Pejcinovic 24
25 at any point is: = Le 2d = Le 2d 6 2d = jlj e 2d 6 (L2d)(33) Input wave attenuated by e d on the way to load; Interpretation: shifted by l. After reection attenuated by another e d phase ) total=e 2d. Only a fraction reected as determined by L. input terminals the mag. of re. wave is j L je 2l. Phase On = 2l but L adds its own ) total = L 2l. shift = ; jj is independent of d but phase angle is still function For d. of Microwave Circuit Design I cb. Pejcinovic 25
26 = ) ^V L = ^V + el [1 + L ] ^IL = ^I + el [1 L ] (34) d ) Z L = ^VL L Z L Z = = Z + ZL where Y L = 1=Z L 1 + L or = Z L 1 ^IL ZL Z ZL 1 ZL + 1 also L = 1 Y L L = 1 + L = (35) Z L Y L (36) to equations in transient case. Dierence is in steady Analogous a.c. analysis ) valid for any complex load. Also merger state a.c. circuit theory (impedance) and wave theory (re. coecient). of Microwave Circuit Design I cb. Pejcinovic 26
27 Extend the concept to any point on the tr. line: Z = 1 (d) and Y = Y 1 (d) ^V 1 + (d) Z = ^I 1 + (d) Represents total Z or Y to the right of point d. (37) means standing waves. When Z L 6= Z ) L 6= and Reection waves exist. standing the short circuit (S-C) load: same as wave reection of Take conductor. see g. 2{24 2{25. Successive minima are perfect =2 apart I shifted by =4 relative to V. Microwave Circuit Design I cb. Pejcinovic 27
28 General case: ^V is sum of phasor quantities ^V + + ^V. case: two counter-rotating vectors of xed magnitude Lossless 2{28). When in phase! maximum (g. V max = V + + jjv + = (1 + jj)v + (38) =4 away there is a minimum (phasors 18 out of phase) V min = V + jjv + = (1 jj)v + (39) Standing wave ratio = max SWR = V 1 + jj min V 1 jj jj = SWR 1 and + 1 SWR Microwave Circuit Design I cb. Pejcinovic 28 (4)
29 For lossless line SWR=const. but not otherwise (not useful). example 3.2 Special Cases Short circuit: Z L = ) L = 1; SWR = 1. At d= A) V=; other nulls occur at multiple of =2. (z=l) I is maximum at the load (d=) its rms value is 2I +. V and I are displace by =4 at d = =4 we have Z! 1 Since short circuit is transformed into open circuit!!! i.e. Open circuit: Y L = ; L = 1; SWR = 1. See g. 3{11 B) standing waves. At d= I=; Vmax = 2V + and at d = =4 for we have Z = i.e. O-C becomes S-C!!! Microwave Circuit Design I cb. Pejcinovic 29
30 C) Reactive loads: ZL = jx ) L = j X 1 X = +1 {z } For?? j X + 1 = arctan X (41) L = 16 9 ; for X = 1 {z } )?? either case jj = 1;SWR! 1. ) L = In reactance cannot absorb power ) all power in incident Interpret: wave must be reected (analogous to S-C and O-C in this Consequence: jlj < 1 only if ZL has a resistive component. respect). 3{12 for SW pattern (ZL = jz ); rst voltage null is 3=8 Fig. from d= away Microwave Circuit Design I cb. Pejcinovic 3
31 D) Resistive loads: L R L Z = real (42) ) Z + RL For RL = Z ) no reections. R L > Z ) L > V max and I min are at the load. (why?) For = RL=Z. SWR R L < Z ) L < and V min ;I min at the load. SWR = For L Z=R SWR = R L =Z or Z =R L whichever is > 1. j L j < 1 i.e. some power is absorbed. Microwave Circuit Design I cb. Pejcinovic 31
32 1.5 Power ow Generally P = Re( ^V ^I ) = V I cos pf of from generator to load ^V = ^V + ez + ^V ez = Direction ow + + ) and ^I = ^I + + ^I = I (1 ) (1 ^V power becomes The + )(1 ) ^V + ^I + # "(1 P = Re = Re (1 + )(1 ) 2 ^V + V + Z 6 64 (1 + jj+ 2 ) jv + j 2 Re = Z (43) Low-loss high freq. ) Z is real ) is imaginary. Microwave Circuit Design I cb. Pejcinovic 32
33 = (1 jj 2 ) jv + j 2 Z P = (1 jj 2 )P + = P + jj 2 P + = P + P Z real net power ow at any point on the line is the difference For between the power in the forward wave P + and in the reected wave P. Note: is function of position. How about input terminals: = P + in (1 j inj 2 ) P L = P + L (1 j Lj 2 ) (44) Pin Remember that + and - signs indicate traveling waves. + in = ( P magn: } { z + ) 2 =Z ; P + L = V +2 L =Z = P + ine 2l (45) V Microwave Circuit Design I cb. Pejcinovic 33
34 incident power at the load is input power attenuated along i.e. line of length l. For lossless lines ) P + in = P + L = P + the power ow is position dependent and we need to determine NET + at any point. P real Z ^V + ; ^I + are in phase ) P + = V +2 For Z V + 2 e 2z = + and its rms value V + are obtained from Kircho's laws at ^V input: = ^Vin + ^IinZG = ( ^V + + in ^V +) + ZG ^VG Microwave Circuit Design I cb. Pejcinovic 34 Z + in ^V + ^V Z (46)
35 + = ^V ^VG Z (ZG + Z )(1 GLe 2l ) where L = (Z G Z )=(Z G + Z ) ^V G ;Z G ;Z L (circuit) and Z ;;l (line) we can nd V +. Given Alternative form: + = ^V (1 G ) ^VG G in ) = 2(1 ^VG (1 G ) 2(1 G L e 2l ) V + known P can be determined. With Microwave Circuit Design I cb. Pejcinovic 35 (47) (48)
36 dierent approaches: a) multiple reection b) steady state Two circuit. What's the relationship? a.c. 1) Either L = or G = so no multiple reections case Initial forward traveling wave from voltage divider Z G +Z occur. ^V + = ^VGZ =(ZG + Z ). Same as in eq. (47). ) 2) Multiple reections. ^V + represents phasor sum of all the case forward traveling waves at input (z=). wave: ^V + (1) = ^V G Z =(Z G + Z ) Initial one: ^V + (2) = G L e 2l ^VG Z =(Z G + Z ) 2nd one: ^V + (3) = ( G L e 2l ) 2 ^V G Z =(Z G + Z ) 3rd etc. Microwave Circuit Design I cb. Pejcinovic 36
37 result is the sum of all of the above; limit of the series is Final j L G e 2l j < 1) is (1 L G e 2l ) 1. This leads to the (when same expression as in a.c. theory (eq. (47)). to power calculation: P + = V +2 e 2z =Z. Now plug in Back for V + expr. + = V 2 G P 4Z (eq. 48)) 1 G so for z= we have + in = V 2 G P 4Z 1 Gin 1 G G in {z } 1 2 e 2z (49) 2 2l e L = Microwave Circuit Design I cb. Pejcinovic 37 (5)
38 concept: available power from source P A = V 2 G=(4R G ) Useful R G = Re(Z G ) where + in = P A P 1 j G j 2 j1 Ginj 2 (51) Finally what is the NET input power? = + (1 j 2 G (1 j )(1 j 2 j in j 2 ) A P = ) inj in P Pin Power deliver to the load: j1 G in j (52) (1 j G j 2 )(1 j L j 2 ) PL = PA 2l j 2 e 2l (53) GLe j1 Microwave Circuit Design I cb. Pejcinovic 38
39 or for lossless line: (1 jgj 2 )(1 jlj 2 ) Pin = P L = P A j2lj2 (54) e L G j1 In this case j in j = j L j then in = L e j2l that the input is matched ZG = Z then G = and PL Assume of frequency and phase angle l ( =!=v). independent for matched input ^V + = ^V G =2 and P + in = P A = Therefore V 2 G=(4Z ) so that Pin = P A (1 j in j 2 ) and P L = P A e 2l (1 j L j 2 ) (55) Microwave Circuit Design I cb. Pejcinovic 39
40 line generator end matched; if load is matched as well Lossless all of PA is delivered to load PL = PA. ) Z G 6= Z it does not follow that matching the load will For P L = P A (see eq. 54). Maximizing power transfer more produce complicated. Example 3-3. Return loss: LR = 1 log(p + =P ) db. Since P = jj 2 P + = log 1 LR 2 db jj (56) lossless line L R is the same anywhere (i.e. jj is independent For position). of Microwave Circuit Design I cb. Pejcinovic 4
41 line means position dependent L R but it is easily determined Lossy from jj = j L je 2d. For input we have in = j L je 2l 6 L 2l so that L R;in = L R;load + 2(8:686l) loss: used only when Z G = Z. Measures reduction in Reection power due to mismatch of load impedance (Z L 6= Z ) load Ref. loss = 1 log aka mismatch loss. A e 2l =P } { z L = Z ) PL(Z L ) PL(Z {z } =P A e 2l (1j L j 2 ) db = 1 log Microwave Circuit Design I cb. Pejcinovic 41 1 j L j 2 (57) 1
42 1.6 Impedance transformation direction; impedance anywhere on line replaces everything Reference to the right. Starting point: 1 + Z Z Z + L e 2d 1 = = 1 1 L e 2d (58) some manipulation (note: bar in e.g. Z = Z=Z is for After values): normalized Z L + Z tanh d Z = Z tanh d ; Z = L Z + Z L + tanh d Z + Z L tanh d 1 Microwave Circuit Design I cb. Pejcinovic 42 (59)
43 or for admitance Y L + Y tanh d Y = Y tanh d ; Y = L Y + Y YL + tanh d + Y L tanh d 1 Input impedance: set d=l; what about d=? If is neglected Z L + jz tan d Z = Z tan d ; Z = L jz + Z and equivalent for Y-s Example 3-4. L + j tan d Z + j Z L tan d 1 Microwave Circuit Design I cb. Pejcinovic 43 (6) (61)
44 changes in Z; standing waves are the cause. No SW ) Dramatic impedance transformation (Z L = Z ) Z = Z anywhere). no happens at LF? l ) tan l so that Z = Z L for What and low loss line. LF Fixed length ) freq. dependence of Z since l =!l=v = 2l= Excellent for impedance transf. but bad for broadband design! =2 line: l = n=2 then Z in = Z L (substitute l = n into eq. 59 ). Impedance repeats itself every =2!! Microwave Circuit Design I cb. Pejcinovic 44
45 Z G = Z L both real (e.g. 2 Ohms). Tr. line has Z = 1 Take and l = =2. SWR = Z =R = 5 but for this lenght of tr. Ohms Z in = Z L = 2 Ohms. All available power is delivered down line lossless line to Z L. Despite SW max. power is delivered to the the load. =4 line: l = (2n 1)=4. Here tan l! 1 and Z in = Z 2 =Z L or normalized Z in = 1= Z L. Large Z L! small Z in and inverse. Inductive Z L! capacitive Z in (and inverse) Z L behaves as a series resonant circuit Z in is like parallel res. If circuit. Microwave Circuit Design I cb. Pejcinovic 45
46 ZL real it behaves like a transformer with turns ratio nt = For SWR) for Z L < Z. But for Z L > Z ;n t < 1. 5(= for matching a resistive load to generator (to deliver all Useful power). For Z G real Z in must be real and Z in = R G or available Z = p R G R L. Since line is assumed lossless all power is delivered to the load. Problem: works only at one (narrow range of) frequency. Microwave Circuit Design I cb. Pejcinovic 46
47 Short circuit: obviously Zin = jxin = jz tan l. See g For l < =2 (or l < =4) Z in is inductive. X in =! = Z tan(l)=! Z l=v = L l Leq = } {z for l<:8 (62) that L eq is freq. dependent. Think of this circuit as one turn note a coil (L). of l = n=2 and odd multiples S-C behaves like parallel Near circuit. resonant l = n S-C behaves like a series resonant circuit. see g. Near Microwave Circuit Design I cb. Pejcinovic 47
48 number of resonances. Note on lenght: go for the shortest Innite... one circuit: use admitances Y L = and Y in = jb in = jy tan l Open Z in = jz cot l. Fig. 3-16; or For l < =4 = Y tan(l)=![f ] Y l=v Ceq {z } l<:8 = l=(z v) = C l (63) again it is freq. dependent; it looks like a parallel plate capacitor. l = = 2l= (i.e. l = =2) we have Y in = (O-C) but For l = (2n 1)=4 Y in = 1 (S-C). for Microwave Circuit Design I cb. Pejcinovic 48
49 1) near l = (2n1)=2 O-C behaves like series resonant circuit 2) near l = n O-C looks like parallel resonant circuit. Microwave Circuit Design I cb. Pejcinovic 49
STORY NAME: Young musician COPYRIGHT HOLDER: COPYRIGHT NOTICE: Telefilm Chisinau / OPEN Media Hub Ownership of content belongs to Telefilm Chisinau /
 STORY NAME: Young musician COPYRIGHT HOLDER: COPYRIGHT NOTICE: Telefilm Chisinau / OPEN Media Hub Ownership of content belongs to Telefilm Chisinau / OPEN Media Hub USAGE TERMS: Share & Adapt - Attribution
STORY NAME: Young musician COPYRIGHT HOLDER: COPYRIGHT NOTICE: Telefilm Chisinau / OPEN Media Hub Ownership of content belongs to Telefilm Chisinau / OPEN Media Hub USAGE TERMS: Share & Adapt - Attribution
TEZA de ABILITARE Corelatii intre biomateriale, proteze valvulare cardiace si tehnici chirurgicale folosite in protezarea valvulara aortica Horatiu Mo
 TEZA de ABILITARE Corelatii intre biomateriale, proteze valvulare cardiace si tehnici chirurgicale folosite in protezarea valvulara aortica Horatiu Moldovan Rezumat Teza de abilitare cu titlul Corelaţii
TEZA de ABILITARE Corelatii intre biomateriale, proteze valvulare cardiace si tehnici chirurgicale folosite in protezarea valvulara aortica Horatiu Moldovan Rezumat Teza de abilitare cu titlul Corelaţii
STORY NAME: Being 20: Japanese culture and Game Development in Moldova COPYRIGHT HOLDER: COPYRIGHT NOTICE: Gabriel Encev / OPEN Media Hub Ownership of
 STORY NAME: Being 0: Japanese culture and Game Development in Moldova COPYRIGHT HOLDER: COPYRIGHT NOTICE: Gabriel Encev / OPEN Media Hub Ownership of content belongs to Gabriel Encev / OPEN Media Hub USAGE
STORY NAME: Being 0: Japanese culture and Game Development in Moldova COPYRIGHT HOLDER: COPYRIGHT NOTICE: Gabriel Encev / OPEN Media Hub Ownership of content belongs to Gabriel Encev / OPEN Media Hub USAGE
IBR 8 iulie 2019
 Managementul riscului în administrarea rezervelor internaționale Victor Andrei * BNR *Direcţia operaţiuni de piaţă Bucureşti * 8 iulie 2019 Opiniile exprimate sunt ale mele și nu reprezintă în mod necesar
Managementul riscului în administrarea rezervelor internaționale Victor Andrei * BNR *Direcţia operaţiuni de piaţă Bucureşti * 8 iulie 2019 Opiniile exprimate sunt ale mele și nu reprezintă în mod necesar
Fişă tehnică produs Caracteristici RM4UB35 single-phase network control relay RM4-U - range V Caracteristici Principale Gama de produse Tip p
 Fişă tehnică produs Caracteristici RM4UB35 single-phase network control relay RM4-U - range 160..220 V Caracteristici Principale Gama de produse Tip produs sau componenta Tip releu Nume releu Zelio Control
Fişă tehnică produs Caracteristici RM4UB35 single-phase network control relay RM4-U - range 160..220 V Caracteristici Principale Gama de produse Tip produs sau componenta Tip releu Nume releu Zelio Control
Fişă tehnică produs Caracteristici RM4JA32MW current measurement relay RM4-J - range A V AC DC Caracteristici Principale Gama de pro
 Fişă tehnică produs Caracteristici RM4JA32MW current measurement relay RM4-J - range 0.3..15 A - 24..240 V AC DC Caracteristici Principale Gama de produse Tip produs sau componenta Tip releu Nume releu
Fişă tehnică produs Caracteristici RM4JA32MW current measurement relay RM4-J - range 0.3..15 A - 24..240 V AC DC Caracteristici Principale Gama de produse Tip produs sau componenta Tip releu Nume releu
Manual de utilizare Set volan și pedale MG7402
 Manual de utilizare Set volan și pedale MG7402 RO MG7402 - Manual de utilizare I. Introducere Vă mulțumim pentru achiziționarea acestui volan de curse realizat pentru console PC. Forma acestuia este asemănătoare
Manual de utilizare Set volan și pedale MG7402 RO MG7402 - Manual de utilizare I. Introducere Vă mulțumim pentru achiziționarea acestui volan de curse realizat pentru console PC. Forma acestuia este asemănătoare
Microsoft Word TURISM - cty_pa_final.doc
 CAPITOLUL 19 TURISM CHAPTER 19 TOURISM Sursa datelor: Cercetări statistice: Cercetări statistice privind activitatea de turism a persoanelor juridice şi fizice care deţin structuri de cazare turistică
CAPITOLUL 19 TURISM CHAPTER 19 TOURISM Sursa datelor: Cercetări statistice: Cercetări statistice privind activitatea de turism a persoanelor juridice şi fizice care deţin structuri de cazare turistică
Inferenţa statistică
 Tudor Drugan 1 Avihu Boneh As for cholesterol, there have been many studies showing clear association between high cholesterol and coronary heart disease. Unfortunately, the correlation is and will be
Tudor Drugan 1 Avihu Boneh As for cholesterol, there have been many studies showing clear association between high cholesterol and coronary heart disease. Unfortunately, the correlation is and will be
PowerPoint Presentation
 MODULUL 4: COSTUL PE DURATA DE VIATA & APLICATII PRACTICE ALE CVD The sole responsibility for the content of this presentation lies with the Clean Fleets project. It does not necessarily reflect the opinion
MODULUL 4: COSTUL PE DURATA DE VIATA & APLICATII PRACTICE ALE CVD The sole responsibility for the content of this presentation lies with the Clean Fleets project. It does not necessarily reflect the opinion
OPTICS User Manual v1.3.1
 HCP Full Name (Art 1.01) DISCLOSURE OF PAYMENTS TO HEALTHCARE PROFESSIONALS (HCPs), AND HEALTHCARE ORGANISATIONS (HCOs) Article 2 - Section 2.03 & Schedule 2 & Clause 24 HCPs: City of HCOs: city where
HCP Full Name (Art 1.01) DISCLOSURE OF PAYMENTS TO HEALTHCARE PROFESSIONALS (HCPs), AND HEALTHCARE ORGANISATIONS (HCOs) Article 2 - Section 2.03 & Schedule 2 & Clause 24 HCPs: City of HCOs: city where
LOADS AND RESULTS ON CFD PROPELER ANALYSIS LOADS AND RESULTS ON CFD PROPELER ANALYSIS Șef lucr. dr. ing. Adrian POPA, Șef lucr. dr. ing. Ionuț Cristia
 LOADS AND RESULTS ON CFD PROPELER ANALYSIS Șef lucr. dr. ing. Adrian POPA, Șef lucr. dr. ing. Ionuț Cristian SCURTU Academia Navală Mircea cel Bătrân, Constanța, România REZUMAT. Pentru a putea determina
LOADS AND RESULTS ON CFD PROPELER ANALYSIS Șef lucr. dr. ing. Adrian POPA, Șef lucr. dr. ing. Ionuț Cristian SCURTU Academia Navală Mircea cel Bătrân, Constanța, România REZUMAT. Pentru a putea determina
User guide
 1 Avatar VR Glasses User Manual Contents English... 4 Avatar VR glasses... 4 How to use... 5 Finding apps... 6 Inserting smartphone... 6 Using a Gamepad... 6 Warnings... 7 2 Romanian... 8 Ochelari realitate
1 Avatar VR Glasses User Manual Contents English... 4 Avatar VR glasses... 4 How to use... 5 Finding apps... 6 Inserting smartphone... 6 Using a Gamepad... 6 Warnings... 7 2 Romanian... 8 Ochelari realitate
Assessment of patients' satisfaction in a public health service
 ASSESSMENT OF PATIENTS' SATISFACTION IN A PUBLIC HEALTH SERVICE Rusu Ionut. MD Bucharest Emergency University Hospital Carol Davila University of Medicine and Pharmacy, Bucharest total amount of population
ASSESSMENT OF PATIENTS' SATISFACTION IN A PUBLIC HEALTH SERVICE Rusu Ionut. MD Bucharest Emergency University Hospital Carol Davila University of Medicine and Pharmacy, Bucharest total amount of population
1 Smartree Romania
 SMART UPDATE 28/01/2013 Buletin informativ de noutăţi legislative referitoare la legislaţia muncii, reglementări fiscale şi alte acte normative care vizează managementul resurselor umane Legislative new
SMART UPDATE 28/01/2013 Buletin informativ de noutăţi legislative referitoare la legislaţia muncii, reglementări fiscale şi alte acte normative care vizează managementul resurselor umane Legislative new
Microsoft Word - text.doc
 MODELAREA ŞI PROIECTAREA FILTRELOR DE REŢEA UTIZATE PENTRU ATENUAREA RIPLURILOR DE CURENT Conf. univ. dr. ing. Lucian MIHEŢ-POPA Universitatea Politehnica din Timişoara Absolvent al Facultăţii de Electrotehnică-Timişoara,
MODELAREA ŞI PROIECTAREA FILTRELOR DE REŢEA UTIZATE PENTRU ATENUAREA RIPLURILOR DE CURENT Conf. univ. dr. ing. Lucian MIHEŢ-POPA Universitatea Politehnica din Timişoara Absolvent al Facultăţii de Electrotehnică-Timişoara,
Microsoft Word - AIC A04 - VFR CHART ENG doc
 Headquarters 10. Ion Ionescu de la Brad Blvd., PO Box 18-90 013813 Bucharest, Romania phone: (+4021) 208 31 00 fax: (+4021) 230 24 42 AFTN: LRBBRTYD e-mail: romatsa.office@romatsa.ro www.romatsa.ro AIM
Headquarters 10. Ion Ionescu de la Brad Blvd., PO Box 18-90 013813 Bucharest, Romania phone: (+4021) 208 31 00 fax: (+4021) 230 24 42 AFTN: LRBBRTYD e-mail: romatsa.office@romatsa.ro www.romatsa.ro AIM
Example Title with Registration Microsoft® and Trademark SQL ServerTM
 802.1x şi NAP 12 aprilie 2010 Cuprins EAP 802.1x Supplicant Pass-through authenticator Authentication server NAP Client Server 802.1x şi NAP 2 Extensible Authentication Protocol Standard IETF (RFC 3748)
802.1x şi NAP 12 aprilie 2010 Cuprins EAP 802.1x Supplicant Pass-through authenticator Authentication server NAP Client Server 802.1x şi NAP 2 Extensible Authentication Protocol Standard IETF (RFC 3748)
consideratii privind analiza statica
 CONSIDERATII PRIVIND EVALUAREA VIBRATIILOR INDUSE IN SCOP TERAPEUTIC IN ORGANISMUL UMAN Florin Bausic - prof. univ.dr.ing. - U.T.C. Bucuresti Abstract Modal analysis methods have been used in the biomechanics
CONSIDERATII PRIVIND EVALUAREA VIBRATIILOR INDUSE IN SCOP TERAPEUTIC IN ORGANISMUL UMAN Florin Bausic - prof. univ.dr.ing. - U.T.C. Bucuresti Abstract Modal analysis methods have been used in the biomechanics
COD 20 SITUAŢIA VENITURILOR SI CHELTUIELILOR la data de / INCOME AND EXPENSES STATEMENT as at Denumirea indicatorilor / Descripti
 COD 0 SITUAŢIA VENITURILOR SI CHELTUIELILOR la data de 3..05/ INCOME AND EXPENSES STATEMENT as at 3..05 Denumirea indicatorilor / Description Nr rand / Row Perioada de raportare / Year ended An An curent
COD 0 SITUAŢIA VENITURILOR SI CHELTUIELILOR la data de 3..05/ INCOME AND EXPENSES STATEMENT as at 3..05 Denumirea indicatorilor / Description Nr rand / Row Perioada de raportare / Year ended An An curent
-. 4 CALITATEA TENSIUNII - CRITERIU PRINCIPAL DE ANALIZĂ A INTERDEPENDENTEI DINTRE ' COMPENSAREA PUTERII REACTIVE, ECHILIBRAREA SARCINII ŞI FILTRAREA
 -. 4 CALITATEA TENSIUNII - CRITERIU PRINCIPAL DE ANALIZĂ A INTERDEPENDENTEI DINTRE ' COMPENSAREA PUTERII REACTIVE, ECHILIBRAREA SARCINII ŞI FILTRAREA ARMONICILOR IN " RETELELE ' DE DISTRIBUTIE PERFORMANTE
-. 4 CALITATEA TENSIUNII - CRITERIU PRINCIPAL DE ANALIZĂ A INTERDEPENDENTEI DINTRE ' COMPENSAREA PUTERII REACTIVE, ECHILIBRAREA SARCINII ŞI FILTRAREA ARMONICILOR IN " RETELELE ' DE DISTRIBUTIE PERFORMANTE
EN_VI_2019_Limba_comunicare_test_2_engleza
 EVALUARE NAŢIONALĂ LA FINALUL CLASEI a VI-a 2019 Test 2 Limbă şi comunicare - Limba engleză Judeţul/sectorul... Localitatea... Unitatea de învățământ... Numele şi prenumele elevului/elevei...... Clasa
EVALUARE NAŢIONALĂ LA FINALUL CLASEI a VI-a 2019 Test 2 Limbă şi comunicare - Limba engleză Judeţul/sectorul... Localitatea... Unitatea de învățământ... Numele şi prenumele elevului/elevei...... Clasa
Brosura Rigcert_RO
 SERVICII DE CERTIFICARE Partener pentru cerificare Noi suntem De ce să lucrezi cu noi? E simplu... Știm că rolul auditurilor este de a vă ajuta să vă îmbunătățiți. Cunoaștem bine cerințele pieței din România.
SERVICII DE CERTIFICARE Partener pentru cerificare Noi suntem De ce să lucrezi cu noi? E simplu... Știm că rolul auditurilor este de a vă ajuta să vă îmbunătățiți. Cunoaștem bine cerințele pieței din România.
Slide 1
 Note de curs Iasi, 27-28 feb. 2008 Analiza materialelor prin difractometrie de radiatii X Obiective: de a cunoaste principiile de baza privind analiza WAXD de a cunoaste principiul de functionare a unui
Note de curs Iasi, 27-28 feb. 2008 Analiza materialelor prin difractometrie de radiatii X Obiective: de a cunoaste principiile de baza privind analiza WAXD de a cunoaste principiul de functionare a unui
I. Navigating LabVIEW
 III. Implementarea unui VI În acest capitol este prezentat modul de implementare a codurilor în LabVIEW. Astfel, acest capitol cuprinde: proiectarea interfeței utilizator (PF); alegerea între diferitele
III. Implementarea unui VI În acest capitol este prezentat modul de implementare a codurilor în LabVIEW. Astfel, acest capitol cuprinde: proiectarea interfeței utilizator (PF); alegerea între diferitele
Microsoft Word - Revista_Universul_Juridic_nr_ _PAGINAT_.doc
 Revista 60 Universul Juridic nr. 12, decembrie 2018, pp. 60-66 SILVIU-DORIN ȘCHIOPU ABSENŢA OBLIGAŢIEI DE INFORMARE ATUNCI CÂND PERSOANA VIZATĂ DEŢINE DEJA RESPECTIVELE INFORMAŢII SAU PRELUCRAREA DATELOR
Revista 60 Universul Juridic nr. 12, decembrie 2018, pp. 60-66 SILVIU-DORIN ȘCHIOPU ABSENŢA OBLIGAŢIEI DE INFORMARE ATUNCI CÂND PERSOANA VIZATĂ DEŢINE DEJA RESPECTIVELE INFORMAŢII SAU PRELUCRAREA DATELOR
Slide 1
 ELECTROTEHNCĂ ET An - SA CRS 8 Conf.dr.ing.ec. Claudia PĂCRAR e-mail: Claudia.Pacurar@ethm.utcluj.ro . ntroducere în teoria circuitelor electrice. Puteri în regim armonic 3. Caracterizarea în complex a
ELECTROTEHNCĂ ET An - SA CRS 8 Conf.dr.ing.ec. Claudia PĂCRAR e-mail: Claudia.Pacurar@ethm.utcluj.ro . ntroducere în teoria circuitelor electrice. Puteri în regim armonic 3. Caracterizarea în complex a
Slide 1
 Curs 1 17 Octombrie 2011 Adrian Iftene adiftene@info.uaic.ro SWEBOK: locul şi rolul ingineriei programării, arii tematice, discipline înrudite Dezvoltarea şi mentenanţa sistemelor:dezvoltare agilă condusă
Curs 1 17 Octombrie 2011 Adrian Iftene adiftene@info.uaic.ro SWEBOK: locul şi rolul ingineriei programării, arii tematice, discipline înrudite Dezvoltarea şi mentenanţa sistemelor:dezvoltare agilă condusă
njoy PSU User Manual Manual de utilizare Before using this product, carefully read all product documentation and retain it for future reference.
 njoy PSU User Manual Manual de utilizare Before using this product, carefully read all product documentation and retain it for future reference. Thank you for purchasing our products! Please read this
njoy PSU User Manual Manual de utilizare Before using this product, carefully read all product documentation and retain it for future reference. Thank you for purchasing our products! Please read this
Untitled-1
 Willbrook Platinum Business & Convention Center Sos. Bucuresti-Ploiesti nr. 172-176, cladirea A, etaj 3, sector 1, Bucuresti. www.theta.com.ro office@theta.com.ro & more documenta on Theta Company profile
Willbrook Platinum Business & Convention Center Sos. Bucuresti-Ploiesti nr. 172-176, cladirea A, etaj 3, sector 1, Bucuresti. www.theta.com.ro office@theta.com.ro & more documenta on Theta Company profile
IR Update February 2014
 Cum poti afla mai multe informatii despre pietele de capital Zuzanna Kurek, Specialist IR Fluent in Finante www.fluentinfinante.ro Crearea unei umbrele cu toate proiectele pietei de capital Platforma
Cum poti afla mai multe informatii despre pietele de capital Zuzanna Kurek, Specialist IR Fluent in Finante www.fluentinfinante.ro Crearea unei umbrele cu toate proiectele pietei de capital Platforma
Realizarea fizică a dispozitivelor optoeletronice
 Curs 08/09 C/L Optoelectronică OPTO Minim 7 prezente curs + laborator Curs - conf. Radu Damian an IV μe Vineri 8-, P5 E 70% din nota 0% test la curs, saptamana 4-5? probleme + (? subiect teorie) + (p prez.
Curs 08/09 C/L Optoelectronică OPTO Minim 7 prezente curs + laborator Curs - conf. Radu Damian an IV μe Vineri 8-, P5 E 70% din nota 0% test la curs, saptamana 4-5? probleme + (? subiect teorie) + (p prez.
ERASMUS RO01-KA IULIE 2018 IANUARIE 2019 ACTIVE CITIZENSHIP ÎN CIFRE 6 luni de proiect, 6 clipuri, 7 organizații partenere din 7 țăr
 ERASMUS+ 2018-1-RO01-KA105-048936 IULIE 2018 IANUARIE 2019 ACTIVE CITIZENSHIP ÎN CIFRE 6 luni de proiect, 6 clipuri, 7 organizații partenere din 7 țări, 7 pagini de internet, 8 stakeholderi, peste 21 activități
ERASMUS+ 2018-1-RO01-KA105-048936 IULIE 2018 IANUARIE 2019 ACTIVE CITIZENSHIP ÎN CIFRE 6 luni de proiect, 6 clipuri, 7 organizații partenere din 7 țări, 7 pagini de internet, 8 stakeholderi, peste 21 activități
PAGINA DE START > PRODUSE > Sisteme de protecţie împotriva incendiilor şi a fumului > Clapete de control fum > Type EK-EU TIP EK-EU PENTRU A FI UTILIZ
 TIP EK-EU PENTRU A FI UTILIZATĂ ÎN SISTEMELE MECANICE DE EXTRACŢIE A FUMULUI ȘI CA O INTRARE ADIŢIONALĂ DE FURNIZARE A AERULUI ȘI, DE ASEMENEA, PENTRU SISTEMELE NATURALE DE EXTRAGERE A FUMULUI ȘI CĂLDURII
TIP EK-EU PENTRU A FI UTILIZATĂ ÎN SISTEMELE MECANICE DE EXTRACŢIE A FUMULUI ȘI CA O INTRARE ADIŢIONALĂ DE FURNIZARE A AERULUI ȘI, DE ASEMENEA, PENTRU SISTEMELE NATURALE DE EXTRAGERE A FUMULUI ȘI CĂLDURII
Personal Scrisori Scrisori - Adresa Română Andreea Popescu Str. Reşiţa, nr. 4, bloc M6, sc. A, ap. 12. Turnu Măgurele Jud. Teleorman România. E
 - Adresa Andreea Popescu Str. Reşiţa, nr. 4, bloc M6, sc. A, ap. 12. Turnu Măgurele Jud. Teleorman 06102. România. Mr. N. Summerbee 335 Main Street New York NY 92926 Formatul românesc de adresă: Strada,
- Adresa Andreea Popescu Str. Reşiţa, nr. 4, bloc M6, sc. A, ap. 12. Turnu Măgurele Jud. Teleorman 06102. România. Mr. N. Summerbee 335 Main Street New York NY 92926 Formatul românesc de adresă: Strada,
Microsoft Word - Silion_Neo_Simina1.doc
 Lucrări ştiinţifice Zootehnie şi Biotehnologii, vol. 40(1), (2007), Timişoara. THE EFFECT OF DIET SULEMENTATION WITH TWO LEVELS OF MANNANOLIGOSACCHARIDE ON THE ERFORMANCE OF GROWING RABBITS EFECTUL A DOUĂ
Lucrări ştiinţifice Zootehnie şi Biotehnologii, vol. 40(1), (2007), Timişoara. THE EFFECT OF DIET SULEMENTATION WITH TWO LEVELS OF MANNANOLIGOSACCHARIDE ON THE ERFORMANCE OF GROWING RABBITS EFECTUL A DOUĂ
Microsoft Word - Revista_Universul_Juridic_nr_3-2019_PAGINAT_.doc
 Revista 64 Universul Juridic nr. 3, martie 2019, pp. 64-70 SILVIU-DORIN ŞCHIOPU ABSENŢA OBLIGAŢIEI DE INFORMARE ÎN IPOTEZA PREVĂZUTĂ DE ART. 14 ALIN. (5) LIT. B) DIN REGULAMENTUL GENERAL PRIVIND PROTECŢIA
Revista 64 Universul Juridic nr. 3, martie 2019, pp. 64-70 SILVIU-DORIN ŞCHIOPU ABSENŢA OBLIGAŢIEI DE INFORMARE ÎN IPOTEZA PREVĂZUTĂ DE ART. 14 ALIN. (5) LIT. B) DIN REGULAMENTUL GENERAL PRIVIND PROTECŢIA
RZOLVARE EXERCITIU ZODII declare cursor distributie_zodie is select nume_zodie, count(*) distributie from zodiac z join utilizatori u on to_date(to_ch
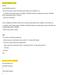 RZOLVARE EXERCITIU ZODII declare cursor distributie_zodie is select nume_zodie, count(*) distributie from zodiac z join utilizatori u on to_date(to_char(u.data_nastere, 'DD-MM'), 'DD-MM') between to_date(z.data_inceput,
RZOLVARE EXERCITIU ZODII declare cursor distributie_zodie is select nume_zodie, count(*) distributie from zodiac z join utilizatori u on to_date(to_char(u.data_nastere, 'DD-MM'), 'DD-MM') between to_date(z.data_inceput,
Societatea Energetică Electrica S.A. Str. Grigore Alexandrescu nr.9, sector , București Tel: , Fax: CIF: RO , J40
 Societatea Energetică Electrica S.A. Str. Grigore Alexandrescu nr.9, sector 1 010621, București Tel: 0212085999, Fax: 0212085998 CIF: RO 13267221, J40/7425/2000 Capital social: 3.459.399.290 LEI www.electrica.ro
Societatea Energetică Electrica S.A. Str. Grigore Alexandrescu nr.9, sector 1 010621, București Tel: 0212085999, Fax: 0212085998 CIF: RO 13267221, J40/7425/2000 Capital social: 3.459.399.290 LEI www.electrica.ro
Ciobanu-R42
 SIM - 3D SOFTWARE VERIFICATION BY FEEDERS FUNCTIONING ANALYSIS VERIFICAREA SOFTULUI SIM 3D PRIN ANALIZA FUNCŢIONĂRII MASELOTELOR Ioan CIOBANU, Aurel CRIŞAN, Tibor BEDŐ, Sorin Ion MUNTEANU, Daniela IONESCU
SIM - 3D SOFTWARE VERIFICATION BY FEEDERS FUNCTIONING ANALYSIS VERIFICAREA SOFTULUI SIM 3D PRIN ANALIZA FUNCŢIONĂRII MASELOTELOR Ioan CIOBANU, Aurel CRIŞAN, Tibor BEDŐ, Sorin Ion MUNTEANU, Daniela IONESCU
07-Marascu_R44
 INCREASING EFFICIENCY OF INDUSTRIAL ENERGY SYSTEMS CREŞTEREA EFICIENŢEI SISTEMELOR ENERGETICE INDUSTRIALE Vladimir MĂRĂSCU-KLEIN Transilvania University of Braşov, Romania Abstract. Increasing energy efficiency
INCREASING EFFICIENCY OF INDUSTRIAL ENERGY SYSTEMS CREŞTEREA EFICIENŢEI SISTEMELOR ENERGETICE INDUSTRIALE Vladimir MĂRĂSCU-KLEIN Transilvania University of Braşov, Romania Abstract. Increasing energy efficiency
Anexa nr. 7 - PV punere in functiune, Certificat de conformitate, Raport calibrare debitmetre
 Anexa nr. 7 - PV punere in functiune, Certificat de conformitate, Raport calibrare debitmetre Automazioni e Sistemi S.r.l. 20867 Caponago - MB - Via delle Gerole 5/A Tel. +39 02-9554.52.1
Anexa nr. 7 - PV punere in functiune, Certificat de conformitate, Raport calibrare debitmetre Automazioni e Sistemi S.r.l. 20867 Caponago - MB - Via delle Gerole 5/A Tel. +39 02-9554.52.1
Analiza modurilor de interpretare ale art. 30 din R1198/2006 şi efectele acestora asupra sectorului de piscicultură Cătălin PLATON
 Analiza modurilor de interpretare ale art. 30 din R1198/2006 şi efectele acestora asupra sectorului de piscicultură Cătălin PLATON 2 a XV-a Reuniune a CM POP, Bucuresti, 18 februarie 2016 3 a XV-a Reuniune
Analiza modurilor de interpretare ale art. 30 din R1198/2006 şi efectele acestora asupra sectorului de piscicultură Cătălin PLATON 2 a XV-a Reuniune a CM POP, Bucuresti, 18 februarie 2016 3 a XV-a Reuniune
Microsoft Word - pensii 4_64_.doc
 Numărul mediu al pensionarilor, (Average number of pensioners, a) Pentru limită de vârstă, (For age limit, IV.1. Numărul mediu al pensionarilor de asigurări sociale de stat şi agricultori Average number
Numărul mediu al pensionarilor, (Average number of pensioners, a) Pentru limită de vârstă, (For age limit, IV.1. Numărul mediu al pensionarilor de asigurări sociale de stat şi agricultori Average number
CAPITOLUL 7
 CAPITOLUL 7 SĂNĂTATE CHAPTER 7 HEALTH Sursa datelor: Cercetări statistice: Cercetări statistice realizate în unităţi sanitare. Surse administrative: Direcţia de Sănătate Publică a Municipiului Bucureşti
CAPITOLUL 7 SĂNĂTATE CHAPTER 7 HEALTH Sursa datelor: Cercetări statistice: Cercetări statistice realizate în unităţi sanitare. Surse administrative: Direcţia de Sănătate Publică a Municipiului Bucureşti
Null
 Manual de utilizare multimetru UT511 CUPRINS INTRODUCERE... 2 INSPECTIA CONTINUTULUI... 2 INFORMATII PRIVIND SIGURANTA... 2 SIMBOLURI ELECTRICE INTERNATIONALE... 3 MODUL SLEEP... 3 INDICATOR STARE BATERIE...
Manual de utilizare multimetru UT511 CUPRINS INTRODUCERE... 2 INSPECTIA CONTINUTULUI... 2 INFORMATII PRIVIND SIGURANTA... 2 SIMBOLURI ELECTRICE INTERNATIONALE... 3 MODUL SLEEP... 3 INDICATOR STARE BATERIE...
GEOGRAFIE
 GEOGRAFIE GEOGRAPHY Tabele: Tables: Pagina Page 1.1 Organizarea administrativă a teritoriului, la 31 Administrative organisation of territory, decembrie 2016... 3 on December 31, 2016 1.2 Temperatura aerului
GEOGRAFIE GEOGRAPHY Tabele: Tables: Pagina Page 1.1 Organizarea administrativă a teritoriului, la 31 Administrative organisation of territory, decembrie 2016... 3 on December 31, 2016 1.2 Temperatura aerului
I. Navigating LabVIEW
 E. Timing a VI Atunci când o buclă termină execuția unei iterații, imediat începe executarea următoarei iterații, bineînțeles dacă nu este întâlnită o condiție de stop. Most often, you need to control
E. Timing a VI Atunci când o buclă termină execuția unei iterații, imediat începe executarea următoarei iterații, bineînțeles dacă nu este întâlnită o condiție de stop. Most often, you need to control
Munca legală, un prim pas spre o pensie decentă Legal work - 1 st step to a proper pension
 Munca legală, un prim pas spre o pensie decentă Legal work - 1 st step to a proper pension DO YOU LIVE & WORKED IN NORWAY AND HAVE WORKED IN ROMANIA too? LOCUIȚI ÎN NORVEGIA ȘI AȚI lucrat ȘI ÎN ROMÂNIA?
Munca legală, un prim pas spre o pensie decentă Legal work - 1 st step to a proper pension DO YOU LIVE & WORKED IN NORWAY AND HAVE WORKED IN ROMANIA too? LOCUIȚI ÎN NORVEGIA ȘI AȚI lucrat ȘI ÎN ROMÂNIA?
MANUALUL UTILIZATORULUI BANCĂ DE ABDOMENE CURBATĂ DHS 1011 NOTIFICĂRI PRIVIND SIGURANȚA Înainte de utilizare, verificați fiecare componentă. Este reco
 MANUALUL UTILIZATORULUI BANCĂ DE ABDOMENE CURBATĂ DHS 1011 NOTIFICĂRI PRIVIND SIGURANȚA Înainte de utilizare, verificați fiecare componentă. Este recomandat să opriți utilizarea în cazul în care există
MANUALUL UTILIZATORULUI BANCĂ DE ABDOMENE CURBATĂ DHS 1011 NOTIFICĂRI PRIVIND SIGURANȚA Înainte de utilizare, verificați fiecare componentă. Este recomandat să opriți utilizarea în cazul în care există
Descoperă lumea din spatele acestei uşi Explore the world behind this door
 Descoperă lumea din spatele acestei uşi Explore the world behind this door FEŢE DE UŞI / DOORKIN DOORAN este marca proprie înregistrată sub care Kastamonu Romania produce și comercializează fețe de uși
Descoperă lumea din spatele acestei uşi Explore the world behind this door FEŢE DE UŞI / DOORKIN DOORAN este marca proprie înregistrată sub care Kastamonu Romania produce și comercializează fețe de uși
1
 ANALIZA REGIMULUI TRANZITORIU DE LUCRU AL UNEI MASINI DE CONSTRUCTII IN VEDEREA STABILIRII ERFORMANTEI TEHNOLOGICE S. l. dr. ing. Carmen Debeleac Universitatea,,Dunarea de Jos din Galati Facultatea de
ANALIZA REGIMULUI TRANZITORIU DE LUCRU AL UNEI MASINI DE CONSTRUCTII IN VEDEREA STABILIRII ERFORMANTEI TEHNOLOGICE S. l. dr. ing. Carmen Debeleac Universitatea,,Dunarea de Jos din Galati Facultatea de
06-Ionescu_R41
 THE VERIFICATION BY THERMAL ANALYSIS OF THE SOFTWARE SIM 3D VERIFICAREA SOFTULUI SIM - 3D PRIN ANALIZĂ TERMICĂ Daniela IONESCU, Ioan CIOBANU, Béla VARGA, Sorin Ion MUNTEANU, Tibor BEDŐ, Aurel CRIŞAN, Vlad
THE VERIFICATION BY THERMAL ANALYSIS OF THE SOFTWARE SIM 3D VERIFICAREA SOFTULUI SIM - 3D PRIN ANALIZĂ TERMICĂ Daniela IONESCU, Ioan CIOBANU, Béla VARGA, Sorin Ion MUNTEANU, Tibor BEDŐ, Aurel CRIŞAN, Vlad
Fişă tehnică produs Caracteristici TWDLCAA16DRF bază extensibilă PLC Twido - sursă V c.a. - 9 I 24 V c.c. - 7 O releu Complementare Logica d
 Fişă tehnică produs Caracteristici TWDLCAA16DRF bază extensibilă PLC Twido - sursă 100...240 V c.a. - 9 I 24 V c.c. - 7 O releu Complementare Logica de intrare discreta Limite pentru tensiune la intrare
Fişă tehnică produs Caracteristici TWDLCAA16DRF bază extensibilă PLC Twido - sursă 100...240 V c.a. - 9 I 24 V c.c. - 7 O releu Complementare Logica de intrare discreta Limite pentru tensiune la intrare
Microsoft Word - 03_Duncea Stefanescu_LegalNews_ RO_EN
 LEGAL NEWS No. 3 / 25 April 2019 Modificări referitoare la legislația zilierilor În Monitorul Oficial nr. 309 / 19.04.2019 a fost publicată OUG 26 (denumită în continuare OUG 26/2019 ) privind modificarea
LEGAL NEWS No. 3 / 25 April 2019 Modificări referitoare la legislația zilierilor În Monitorul Oficial nr. 309 / 19.04.2019 a fost publicată OUG 26 (denumită în continuare OUG 26/2019 ) privind modificarea
Slide 1
 Cursul 10 20 mai Previous courses Testing Test Automation Software Bug Testing cycle Program Quality Metrics Copyright 2 How, Who, When, Where, Results 3 Test Automation: How, Who, When, Results 4 Software
Cursul 10 20 mai Previous courses Testing Test Automation Software Bug Testing cycle Program Quality Metrics Copyright 2 How, Who, When, Where, Results 3 Test Automation: How, Who, When, Results 4 Software
Teste şi Măsurători de CIEM. Introducere în Măsurări Electromagnetice pentru Determinarea Compatibilităţii şi Interferenţei Electro-Magnetice. Metode
 Teste şi Măsurători de CIEM. Introducere în Măsurări pentru Determinarea Compatibilităţii şi Interferenţei Electro- Magnetice. Cuprinsul 1. Introducere 1.1. Fundamentarea Metodelor de Testare 1.2. Proiectarea
Teste şi Măsurători de CIEM. Introducere în Măsurări pentru Determinarea Compatibilităţii şi Interferenţei Electro- Magnetice. Cuprinsul 1. Introducere 1.1. Fundamentarea Metodelor de Testare 1.2. Proiectarea
S.C. "ŞANTIERUL NAVAL ORŞOVA" S.A. Nr. RC J25/150/1991 CIF: RO Capital social: - subscris ,5 lei - varsat ,5 lei Str. Tufă
 S.C. "ŞANTIERUL NAVAL ORŞOVA" S.A. Nr. RC J25/150/1991 CIF: RO 1614734 Capital social: - subscris 28.557.297,5 lei - varsat 28.557.297,5 lei Str. Tufări, nr. 4, Orşova, 225200, Mehedinţi Tel.: 0252/362.399;
S.C. "ŞANTIERUL NAVAL ORŞOVA" S.A. Nr. RC J25/150/1991 CIF: RO 1614734 Capital social: - subscris 28.557.297,5 lei - varsat 28.557.297,5 lei Str. Tufări, nr. 4, Orşova, 225200, Mehedinţi Tel.: 0252/362.399;
rodideal
 Eclectic IM-probabilities R A D U R O D I D E A L 18 septembrie- 13 octombrie 2018 R A D U R O D I D E A L Eclectic IM-probabilities E C L E C T I C I M - P R O B A B I L I T I E S Radu Rodideal, născut
Eclectic IM-probabilities R A D U R O D I D E A L 18 septembrie- 13 octombrie 2018 R A D U R O D I D E A L Eclectic IM-probabilities E C L E C T I C I M - P R O B A B I L I T I E S Radu Rodideal, născut
Slide 1
 Implementarea proiectului PBLMD la Universitatea de Stat din Moldova Şedinţa de monitorizare a proiectului organizată de Oficiul Naţional Erasmus+ May 29, 2017 This project has been funded with support
Implementarea proiectului PBLMD la Universitatea de Stat din Moldova Şedinţa de monitorizare a proiectului organizată de Oficiul Naţional Erasmus+ May 29, 2017 This project has been funded with support
Packet Tracer - Configurarea ACL-urilor extinse - Scenariul 1 Topologie Tabela de Adresare R1 Echipament Interfață Adresă IP Masca de subreţea Default
 Topologie Tabela de Adresare R1 Echipament Interfață Adresă IP Masca de subreţea Default Gateway G0/0 172.22.34.65 255.255.255.224 N/A G0/1 172.22.34.97 255.255.255.240 N/A G0/2 172.22.34.1 255.255.255.192
Topologie Tabela de Adresare R1 Echipament Interfață Adresă IP Masca de subreţea Default Gateway G0/0 172.22.34.65 255.255.255.224 N/A G0/1 172.22.34.97 255.255.255.240 N/A G0/2 172.22.34.1 255.255.255.192
Cartelele telefonice
 Cartelele telefonice Mr.instr. Gheorghe OLAN Generalităţi De la mijlocul anilor 80 a apărut o nouă generaţie de carduri (aşanumitele carduri inteligente sau carduri cu cipuri), care au înlocuit majoritatea
Cartelele telefonice Mr.instr. Gheorghe OLAN Generalităţi De la mijlocul anilor 80 a apărut o nouă generaţie de carduri (aşanumitele carduri inteligente sau carduri cu cipuri), care au înlocuit majoritatea
SILVER collection OMillefiori ID precious murano collections
 SILVER collection OMillefiori ID precious murano collections SILVER collection OMillefiori'"l precious murano collections ... -t;;inuta, stil, con-t;;inut 9i idei, plus carisrna... Sticla "de gheata'~
SILVER collection OMillefiori ID precious murano collections SILVER collection OMillefiori'"l precious murano collections ... -t;;inuta, stil, con-t;;inut 9i idei, plus carisrna... Sticla "de gheata'~
PowerPoint Presentation
 Forme Normale 4 Redundanţa Redundanţa este cauza principală a majorităţii problemelor legate de structura bazelor de date relaţionale: spaţiu utilizat, anomalii de inserare / stergere / actualizare. Redundanţa
Forme Normale 4 Redundanţa Redundanţa este cauza principală a majorităţii problemelor legate de structura bazelor de date relaţionale: spaţiu utilizat, anomalii de inserare / stergere / actualizare. Redundanţa
Folosește legislația ErP în avantajul tău Treci pe tehnologia HID pentru a economisi bani și energie electrică
 Folosește legislația ErP în avantajul tău Treci pe tehnologia HID pentru a economisi bani și energie electrică Schimbă sursele de iluminat pentru a economisi bani și energie electrică Eliminarea treptată
Folosește legislația ErP în avantajul tău Treci pe tehnologia HID pentru a economisi bani și energie electrică Schimbă sursele de iluminat pentru a economisi bani și energie electrică Eliminarea treptată
O teoremă de reprezentare (II) Marian TETIVA 1 Abstract. In this paper some (in general well-known) results on complete sequences are exposed, with ap
 O teoremă de reprezentare (II) Marian TETIVA 1 Abstract. In this paper some (in general well-known) results on complete sequences are exposed, with applications to Erdős-Suranyi sequences. We start from
O teoremă de reprezentare (II) Marian TETIVA 1 Abstract. In this paper some (in general well-known) results on complete sequences are exposed, with applications to Erdős-Suranyi sequences. We start from
Slide 1
 C2 / 5.03.2019 Utilizare soft-uri specializate în Kineto Curs : Marti 12-14 Activităţi: 2 ore curs, 1 ore laborator, (prezenta obligatorie) Mail: Per@cs.ubbcluj.ro, Web: www.cs.ubbcluj.ro/~per, Cursuri
C2 / 5.03.2019 Utilizare soft-uri specializate în Kineto Curs : Marti 12-14 Activităţi: 2 ore curs, 1 ore laborator, (prezenta obligatorie) Mail: Per@cs.ubbcluj.ro, Web: www.cs.ubbcluj.ro/~per, Cursuri
Document1
 Current state of play 23.12.2015 regarding the legal procedure in respect of ASTRA very limited time to address a claim to the Court and the appointed Liquidator On 3 rd December 2015 the Court of First
Current state of play 23.12.2015 regarding the legal procedure in respect of ASTRA very limited time to address a claim to the Court and the appointed Liquidator On 3 rd December 2015 the Court of First
EN_VI_2019_Limba_comunicare_test_1_engleza
 EVALUARE NAŢIONALĂ LA FINALUL CLASEI a VI-a 2019 Test 1 Limbă şi comunicare - Limba engleză Judeţul/sectorul... Localitatea... Unitatea de învățământ... Numele şi prenumele elevului/elevei...... Clasa
EVALUARE NAŢIONALĂ LA FINALUL CLASEI a VI-a 2019 Test 1 Limbă şi comunicare - Limba engleză Judeţul/sectorul... Localitatea... Unitatea de învățământ... Numele şi prenumele elevului/elevei...... Clasa
F O R Ţ A DE M U N C Ă
 TRANSPORTURI, POŞTĂ ŞI TELECOMUNICAŢII Tabele: TRANSPORT, POST AND TELECOMMUNICATIONS Tables: Pagina Page 14.1 Drumurile publice, la 31 Decembrie.. 266 Public roads, on December 31 14.2 Liniile de cale
TRANSPORTURI, POŞTĂ ŞI TELECOMUNICAŢII Tabele: TRANSPORT, POST AND TELECOMMUNICATIONS Tables: Pagina Page 14.1 Drumurile publice, la 31 Decembrie.. 266 Public roads, on December 31 14.2 Liniile de cale
Note: The English version of the Lease Agreement may be found in Section B of this document if necessary. SECȚIUNEA A. CONTRACT DE ÎNCHIRIERE NR. [NR]
![Note: The English version of the Lease Agreement may be found in Section B of this document if necessary. SECȚIUNEA A. CONTRACT DE ÎNCHIRIERE NR. [NR] Note: The English version of the Lease Agreement may be found in Section B of this document if necessary. SECȚIUNEA A. CONTRACT DE ÎNCHIRIERE NR. [NR]](/thumbs/102/155417037.jpg) Note: The English version of the Lease Agreement may be found in Section B of this document if necessary. SECȚIUNEA A. CONTRACT DE ÎNCHIRIERE NR. [NR]/[DATA] Prezentul contract de închiriere ("Contract")
Note: The English version of the Lease Agreement may be found in Section B of this document if necessary. SECȚIUNEA A. CONTRACT DE ÎNCHIRIERE NR. [NR]/[DATA] Prezentul contract de închiriere ("Contract")
Pensii şi asigurări sociale de stat / Pensions and State Social Insurance
 Evoluţii în domeniul asigurărilor sociale de stat Intrarea în vigoare a Legii nr. 263/2010 privind sistemul unitar de pensii publice, a dus la evitarea unor evoluţii negative ale sistemului de pensii publice.
Evoluţii în domeniul asigurărilor sociale de stat Intrarea în vigoare a Legii nr. 263/2010 privind sistemul unitar de pensii publice, a dus la evitarea unor evoluţii negative ale sistemului de pensii publice.
Entrepreneurship and Technological Management
 Platformă de e-learning și curriculă e-content pentru învățământul superior tehnic Proiectarea Algoritmilor 33. Algoritmul de tip Monte Carlo Bibliografie [1] C. Giumale Introducere in Analiza Algoritmilor
Platformă de e-learning și curriculă e-content pentru învățământul superior tehnic Proiectarea Algoritmilor 33. Algoritmul de tip Monte Carlo Bibliografie [1] C. Giumale Introducere in Analiza Algoritmilor
PowerPoint Presentation
 CERTIPRO IC3- Internet & Computing Core Certification David Ford & Gabriela Bunescu Certipro Education and Training CE ESTE CERTIPORT & CERTIPRO? O companie care sprijină educația și tehnologia la nivel
CERTIPRO IC3- Internet & Computing Core Certification David Ford & Gabriela Bunescu Certipro Education and Training CE ESTE CERTIPORT & CERTIPRO? O companie care sprijină educația și tehnologia la nivel
Peer-to-peer strategies for stimulating resource sharing Mircea Bardac Coordonator: Prof. dr. ing. Adina Magda Florea 23 decembrie 2010
 Peer-to-peer strategies for stimulating resource sharing Mircea Bardac Coordonator: Prof. dr. ing. Adina Magda Florea 23 decembrie 2010 Cuprins Motivație Concepte în P2P Provocări în implementarea strategiilor
Peer-to-peer strategies for stimulating resource sharing Mircea Bardac Coordonator: Prof. dr. ing. Adina Magda Florea 23 decembrie 2010 Cuprins Motivație Concepte în P2P Provocări în implementarea strategiilor
untitled
 8 STUDII DE CAZ VARIABILITATEA PE TERMEN SCURT A REZISTENºEI RESPIRATORII DETERMINATÅ PRIN TEHNICA ÎNTRERUPERII FLUXULUI Dr. Sorin C. Man, Dr. Simona A. Tåtar Universitatea de Medicinå şi Farmacie Iuliu
8 STUDII DE CAZ VARIABILITATEA PE TERMEN SCURT A REZISTENºEI RESPIRATORII DETERMINATÅ PRIN TEHNICA ÎNTRERUPERII FLUXULUI Dr. Sorin C. Man, Dr. Simona A. Tåtar Universitatea de Medicinå şi Farmacie Iuliu
Participation on Logiscool Courses and in Camps: General Terms and Conditions (GTC) For the purposes of these General Terms and Conditions, the follow
 Participation on Logiscool Courses and in Camps: General Terms and Conditions (GTC) For the purposes of these General Terms and Conditions, the following words and expressions shall have the following
Participation on Logiscool Courses and in Camps: General Terms and Conditions (GTC) For the purposes of these General Terms and Conditions, the following words and expressions shall have the following
Parenting and Child Sexuality Questionnaire Va ruga m sa citit i fiecare afirmat ie s i sa bifat i un numa r de la 0 la 3 care indica i n ce ma sura a
 Parenting and Child Sexuality Questionnaire Va ruga m sa citit i fiecare afirmat ie s i sa bifat i un numa r de la 0 la 3 care indica i n ce ma sura acea afirmat ie vi se potrives te. Nu exista ra spunsuri
Parenting and Child Sexuality Questionnaire Va ruga m sa citit i fiecare afirmat ie s i sa bifat i un numa r de la 0 la 3 care indica i n ce ma sura acea afirmat ie vi se potrives te. Nu exista ra spunsuri
AUTORITATEA NAȚIONALĂ DE REGLEMENTARE ÎN DOMENIUL ENERGIEI Nota de prezentare a Proiectului de Normă Tehnică privind Cerinţele tehnice de racordare la
 AUTORITATEA NAȚIONALĂ DE REGLEMENTARE ÎN DOMENIUL ENERGIEI Nota de prezentare a Proiectului de Normă Tehnică privind Cerinţele tehnice de racordare la reţelele electrice de interes public pentru module
AUTORITATEA NAȚIONALĂ DE REGLEMENTARE ÎN DOMENIUL ENERGIEI Nota de prezentare a Proiectului de Normă Tehnică privind Cerinţele tehnice de racordare la reţelele electrice de interes public pentru module
UNIVERSITATEA LUCIAN BLAGA DIN SIBIU FACULTATEA DE DREPT SIMION BĂRNUŢIU Sibiu, Calea Dumbrăvii nr.34, Tel./Fax: , drept
 UNIVERSITATEA LUCIAN BLAGA DIN SIBIU FACULTATEA DE DREPT SIMION BĂRNUŢIU 550 Sibiu, Calea Dumbrăvii nr., Tel./Fax: 069 670,69 Email:drept@ulbsibiu.ro Curricula PLAN DE ÎNVĂŢĂMÂNT PROGRAMUL DE STUDII UNIVERSITARE
UNIVERSITATEA LUCIAN BLAGA DIN SIBIU FACULTATEA DE DREPT SIMION BĂRNUŢIU 550 Sibiu, Calea Dumbrăvii nr., Tel./Fax: 069 670,69 Email:drept@ulbsibiu.ro Curricula PLAN DE ÎNVĂŢĂMÂNT PROGRAMUL DE STUDII UNIVERSITARE
