REZOLVAREA UNOR PROBLEME CU AJUTORUL PRINCIPIILOR MECANICII CLASICE
|
|
|
- Felicia Mocanu
- 3 ani în urmă
- Vzualizari:
Transcriere
1 REZOLVAREA UNOR PROBLEME CU AJUTORUL PRINCIPIILOR MECANICII CLASICE 1
2 Problema 1 Determinaţi acceleraţia unui corp de masă m, care alunecă cu frecare pe un plan înclinat de unghi, cunoscând coeficientul de frecare la alunecare. Aplicaţie numerică: = 30 0, = 3/4 2
3 Determinaţi acceleraţia unui corp de masă m, care alunecă cu frecare pe un plan înclinat de unghi, cunoscând 3coeficientul de frecare la alunecare. Aplicaţie numerică: = 300, = /4 F f N 1. Se desenează forţele şi acceleraţia sau sensul mişcării: G Greutatea- spre centrul Pământului; Normala (reacţiunea suprafeţei de sprijin) perpendiculară pe suprafaţa de sprijin; Forţa de frecare opusă mişcării sau tendinţei de mişcare; Acceleraţia 3
4 G F F f G F f mg N m a G N G G G Gsin Gcos Epresia principiul al II-lea!!! 2. Se aleg două ae de coordonate, perpendiculare: *de preferat 0 pe direcţia de mişcare 0 pe directia normalei 3. Se proiectează forţele care nu au aceeaşi direcţie cu aele alese şi se scriu formulele forţelor şi componentele pe ae: 4
5 G F f G G F f =ma N G =0 N G 4. Se scrie principiul al IIlea al dinamicii, pe cele două ae: - Forţele care au sensul de mişcare sau sensul ales convenţional, se consideră pozitive; - Forţele care au sens opus mişcării sau sensului ales convenţional se consideră negative 5
6 5. Se rezolvă sistemul. G F f G N G - De preferat se determină normala din ecuaţia de pe o şi se introduce în relaţia forţei de frecare din ecuaţia pe o G Ff mn G G G ma N G 0 G N ma 6
7 a a a G G m g sin m g cos m m g sin cos m/ s
8 Problema 2 Determinaţi acceleraţia unui corp de masă m, care alunecă cu frecare pe un plan orizontal, sub acţiunea unei forţe F, care face unghiul cu direcţia de mişcare, cunoscând coeficientul de frecare la alunecare. 8
9 Determinaţi acceleraţia unui corp de masă m, care alunecă cu frecare pe un plan orizontal, sub acţiunea unei forţe F, care face unghiul cu direcţia de mişcare, cunoscând coeficientul de frecare la alunecare. Aplicaţie numerică: = 30 0, = 3 /4 F f N G F Se desenează forţele şi acceleraţia sau sensul mişcării: Greutatea- spre centrul Pământului; Normala (reacţiunea suprafeţei de sprijin) perpendiculară pe suprafaţa de sprijin; Forţa de frecare opusă mişcării sau tendinţei de mişcare; Acceleraţia 9
10 Determinaţi acceleraţia unui corp de masă m, care alunecă cu frecare pe un plan orizontal, sub acţiunea unei forţe F, care face unghiul cu direcţia de mişcare, cunoscând coeficientul de frecare la alunecare. Aplicaţie numerică: = 30 0, = 3/4 F f F = F cos F = F sin N F G G F F f F F mg N m a 2. Se aleg două ae de coordonate, perpendiculare: *de preferat 0 pe direcţia de mişcare 0 pe directia normalei 3. Se proiectează forţele care nu au aceeaşi direcţie cu aele alese şi se scriu formulele forţelor şi componentele pe ae: Epresia principiul al II-lea!!! 10
11 Determinaţi acceleraţia unui corp de masă m, care alunecă cu frecare pe un plan orizontal, sub acţiunea unei forţe F, care face unghiul cu direcţia de mişcare, cunoscând coeficientul de frecare la alunecare. Aplicaţie numerică: = 30 0, = 3/4 F f F F f = ma N G N +F G = 0 F F F 4. Se scrie principiul al IIlea al dinamicii, pe cele două ae: - Forţele care au sensul de mişcare sau sensul ales convenţional, se consideră pozitive; - Forţele care au sens opus mişcării sau sensului ales convenţional se consideră negative 11
12 Determinaţi acceleraţia unui corp de masă m, care alunecă cu frecare pe un plan orizontal, sub acţiunea unei forţe F, care face unghiul cu direcţia de mişcare, cunoscând coeficientul de frecare la alunecare. Aplicaţie numerică: = 30 0, = 3/4 F f N F F F 5. Se rezolvă sistemul. - De preferat se determină normala din ecuaţia de pe o şi se introduce în relaţia forţei de frecare din ecuaţia pe o G F F f = ma N +F G = 0 N = G - F F N = ma F (G F) = m a = [F (G F)]/m 12
13 a = [F (G F)]/m a = [F cos (m g Fsin)]/m 13
14 m 2 m 1 Problema 3 Determinaţi acceleraţia sistemului de corpuri din figură, cunoscând coeficientul de frecare la alunecare, al corpului m 1, pe planul înclinat de unghi şi masele corpurilor m 1 şi m 2, şi sensul de mişcare de pe figură Aplicaţie numerică: m1 = 1 Kg, m2= 3 kg, = 30 0, = 1.73/4 14
15 Determinaţi acceleraţia sistemului de corpuri din figură, cunoscând coeficientul de frecare la alunecare, al corpului m 1, pe planul înclinat de unghi şi masele corpurilor m 1 şi m 2, şi sensul de mişcare de pe figură T T m 2 G 2 T m 1 (m 2 ) Greutatea G 2 - spre centrul Pământului; Tensiunea din fir T Acceleraţia a T G 1 N 1 F f 1 1. Se desenează forţele şi acceleraţia sau sensul mişcării pentru fiecare din cele două corpuri: (m 1 ) Greutatea G 1 - spre centrul Pământului; Normala N 1 perpendiculară pe suprafaţa de sprijin; Forţa de frecare F f1 opusă mişcării sau tendinţei de mişcare; Tensiunea din fir T Acceleraţia a 15
16 m 2 Determinaţi acceleraţia sistemului de corpuri din figură, cunoscând coeficientul de frecare la alunecare, al corpului m 1, pe planul înclinat de unghi şi masele corpurilor m 1 şi m 2, şi sensul de mişcare de pe figură T T G 2 T G 1 G 1 = G 1 sin T G 1 = G 1 cos G 1 G G F F m 1 N 1 G f F f 1 m g m g N m a 2. Se aleg două ae de coordonate, perpendiculare, pentru fiecare corp în parte: *de preferat 0 pe direcţia de mişcare 0 pe directia normalei 3. Se proiectează forţele care nu au aceeaşi direcţie cu aele alese şi se scriu formulele forţelor şi componentele pe ae: Epresia principiul al II-lea!!! 16
17 m 2 Determinaţi acceleraţia sistemului de corpuri din figură, cunoscând coeficientul de frecare la alunecare, al corpului m 1, pe planul înclinat de unghi şi masele corpurilor m 1 şi m 2, şi sensul de mişcare de pe figură T T G 2 T G 1 T G 1 (m 1 ) O: T G 1 - F f = m 1 a O: N 1 G 1 = 0 (m 2 ) O: G 2 T = m 2 a O: - m 1 N 1 G 1 F f 1 4. Se scrie principiul al II-lea al dinamicii, pe cele două ae, pentru fiecare corp în parte: - Forţele care au sensul de mişcare sau sensul ales convenţional, se consideră pozitive; - Forţele care au sens opus mişcării sau sensului ales convenţional se consideră negative 17
18 m 2 Determinaţi acceleraţia sistemului de corpuri din figură, cunoscând coeficientul de frecare la alunecare, al corpului m 1, pe planul înclinat de unghi şi masele corpurilor m 1 şi m 2, şi sensul de mişcare de pe figură T T G 2 T G 1 T G 1 (m 1 ) O: T G 1 - F f = m 1 a O: N 1 G 1 = 0 m 1 N 1 G 1 F f 1 N 1 = G 1 5. Se rezolvă sistemul. -De preferat se determină normala din ecuaţia de pe o şi se introduce în relaţia forţei de frecare din ecuaţia pe o; T G 1 - N = m 1 a T G 1 - G 1 = m 1 a (1) (m 2 ) O: G 2 T = m 2 a O: - (2) 18
19 Cu relaţiile (1) şi (2) se formează un sistem din care se determină necunoscutele, în acest caz: a şi T T G 1 - G 1 = m 1 a G 2 T = m 2 a (+) G 2 - G 1 - G 1 = ( m 1 + m 2 ) a a = (G 2 - G 1 - G 1 )/( m 1 + m 2 ) a = (m 2 g - m 1 gsin- m 1 g cos )/( m 1 + m 2 ) Calcul numeric :D 19
Microsoft Word - SUBIECT 2017 anul I.doc
 Subiecte anul I Problema I (10 puncte) Viteza unui vehicul e masă m, care se eplasează rectiliniu, variază upă legea t v c, t une v este viteza, t timpul, iar c şi τ sunt constante pozitive. a) Reprezintă
Subiecte anul I Problema I (10 puncte) Viteza unui vehicul e masă m, care se eplasează rectiliniu, variază upă legea t v c, t une v este viteza, t timpul, iar c şi τ sunt constante pozitive. a) Reprezintă
Complemente de Fizica I Cursul 1
 Complemente de Fizică I Cursul 1 Victor E. Ambruș Universitatea de Vest din Timișoara Capitolul I. Transformări de coordonate I.1. Transformări Galilei. I.2. Spațiul E 3 al vectorilor tridimensionali.
Complemente de Fizică I Cursul 1 Victor E. Ambruș Universitatea de Vest din Timișoara Capitolul I. Transformări de coordonate I.1. Transformări Galilei. I.2. Spațiul E 3 al vectorilor tridimensionali.
MECANICA FLUIDELOR
 MECANICA FLUIDELOR Generalităţi Orice substanţă care curge se numeşte fluid. În această categorie se încadrează atât lichidele cât şi gazele. Deoarece cu gazele se produc de obicei transformări termice,
MECANICA FLUIDELOR Generalităţi Orice substanţă care curge se numeşte fluid. În această categorie se încadrează atât lichidele cât şi gazele. Deoarece cu gazele se produc de obicei transformări termice,
CONCURSUL INTERLICEAL “TOPFIZ”
 INISTERUL EDUCAȚIEI NAȚIONALE INSPECTORATUL ȘCOLAR JUDEȚEAN, BN CENTRUL JUDEȚEAN DE EXCELENȚĂ, BN CONCURS REGIONAL DE FIZICĂ 988 8 C. N. LIIU REBREANU, Bistrița 3 5 noiembrie 8 Clasa a X-a Probleme propuse
INISTERUL EDUCAȚIEI NAȚIONALE INSPECTORATUL ȘCOLAR JUDEȚEAN, BN CENTRUL JUDEȚEAN DE EXCELENȚĂ, BN CONCURS REGIONAL DE FIZICĂ 988 8 C. N. LIIU REBREANU, Bistrița 3 5 noiembrie 8 Clasa a X-a Probleme propuse
Slide 1
 VIII. Reprezentarea şi cotarea organelor de maşini 8.1 ROŢI DINŢTE Roţile dinţate sunt organe de maşini constituite de corpuri de rotaţie (cilindru, con, hiperboloid) prevăzute cu dantură exterioară sau
VIII. Reprezentarea şi cotarea organelor de maşini 8.1 ROŢI DINŢTE Roţile dinţate sunt organe de maşini constituite de corpuri de rotaţie (cilindru, con, hiperboloid) prevăzute cu dantură exterioară sau
Dorel LUCHIAN Gabriel POPA Adrian ZANOSCHI Gheorghe IUREA algebră geometrie clasa a VIII-a ediţia a V-a, revizuită mate 2000 standard EDITURA PARALELA
 Dorel LUCHIAN Gabriel POPA Adrian ZANOSCHI Gheorghe IUREA algebră geometrie clasa a VIII-a ediţia a V-a, revizuită mate 000 standard 3 10 PP Algebră Capitolul I. NUMERE REALE Competenţe specifice: Determinarea
Dorel LUCHIAN Gabriel POPA Adrian ZANOSCHI Gheorghe IUREA algebră geometrie clasa a VIII-a ediţia a V-a, revizuită mate 000 standard 3 10 PP Algebră Capitolul I. NUMERE REALE Competenţe specifice: Determinarea
CATEDRA FIZIOLOGIA OMULUI ŞI BIOFIZICĂ Cerinţele unice pentru lucrările de laborator din ciclul 1, facultatea Medicina Preventiva. (anul universitar 2
 CATEDRA FIZIOLOGIA OMULUI ŞI BIOFIZICĂ Cerinţele unice pentru lucrările de laborator din ciclul 1, facultatea Medicina Preventiva. (anul universitar 2018-2019) Fiecare student trebuie să scrie anticipat
CATEDRA FIZIOLOGIA OMULUI ŞI BIOFIZICĂ Cerinţele unice pentru lucrările de laborator din ciclul 1, facultatea Medicina Preventiva. (anul universitar 2018-2019) Fiecare student trebuie să scrie anticipat
Ministerul Educa iei i Cercet rii Serviciul Na ional de Evaluare i Examinare EXAMENUL DE BACALAUREAT Proba scris la Fizic Proba E: Specializare
 A. MECANIC Se consider accelera ia gravita ional g =0 m/s.. Unitatea de m sur în S.I. pentru energia cinetic este: a. J b. W c. N d. Kg m s. Alege i expresia care are dimensiunea unui impuls mecanic: a.
A. MECANIC Se consider accelera ia gravita ional g =0 m/s.. Unitatea de m sur în S.I. pentru energia cinetic este: a. J b. W c. N d. Kg m s. Alege i expresia care are dimensiunea unui impuls mecanic: a.
MergedFile
 Olimpiada Naţională de Fizică Timișoara 6 Proba teoretică Barem Pagina din X Subiectul Parţial Punctaj. Barem subiectul A. a) phidrostatica gh N/ m p 4 N/ m r pa phidrostatica p 3 A. b) Ec Lgaz LG unde
Olimpiada Naţională de Fizică Timișoara 6 Proba teoretică Barem Pagina din X Subiectul Parţial Punctaj. Barem subiectul A. a) phidrostatica gh N/ m p 4 N/ m r pa phidrostatica p 3 A. b) Ec Lgaz LG unde
Microsoft Word - proiect 2013
 13 4 Temă de proiect TCM, an universitar 2012-2013 Se consideră mecanismul cu camă-tachet axat din Fig. 1. Elementul conducător este cama plana 1, care are profilul un cerc cu raza r=0,072 m. Axa A a cuplei
13 4 Temă de proiect TCM, an universitar 2012-2013 Se consideră mecanismul cu camă-tachet axat din Fig. 1. Elementul conducător este cama plana 1, care are profilul un cerc cu raza r=0,072 m. Axa A a cuplei
PowerPoint Presentation
 Metode de reprezentare a) Metoda E b) Metoda Clasificarea desenelor tehnice dupa modul de reprezentare: a) Desenul în proiectie ortogonala b) Desenul în perspectiva Dispunerea proiecţiilor Tipuri de reprezentări
Metode de reprezentare a) Metoda E b) Metoda Clasificarea desenelor tehnice dupa modul de reprezentare: a) Desenul în proiectie ortogonala b) Desenul în perspectiva Dispunerea proiecţiilor Tipuri de reprezentări
Microsoft Word - Tsakiris Cristian - MECANICA FLUIDELOR
 Cuvânt înainte Acest curs este destinat studenţilor care se specializează în profilul de Inginerie economică industrială al Facultăţii de Inginerie Managerială și a Mediului, care funcţionează în cadrul
Cuvânt înainte Acest curs este destinat studenţilor care se specializează în profilul de Inginerie economică industrială al Facultăţii de Inginerie Managerială și a Mediului, care funcţionează în cadrul
Microsoft Word - L25Ro_Studiul efectului Hall_f_RF
 STUDIUL EFECTULUI ALL 1. Scopul lucrării Obiectivul acestei lucrări este: punerea în evidenţă a efectului all pentru un semiconductor intrinsec, măsurarea tensiunii all, determinarea constantei all, a
STUDIUL EFECTULUI ALL 1. Scopul lucrării Obiectivul acestei lucrări este: punerea în evidenţă a efectului all pentru un semiconductor intrinsec, măsurarea tensiunii all, determinarea constantei all, a
Microsoft Word - onf laborator subiect.doc
 Ministerul Educaţiei, Cercetării, Tineretului şi Sportului Olimpiada de Fizică Etapa Naţională 3 ianuarie 5 februarie 00 Constanţa XII PROBA DE LABORATOR LUCRAREA A STUDIUL MIŞCĂRII OSCILATORII AMORTIZATE
Ministerul Educaţiei, Cercetării, Tineretului şi Sportului Olimpiada de Fizică Etapa Naţională 3 ianuarie 5 februarie 00 Constanţa XII PROBA DE LABORATOR LUCRAREA A STUDIUL MIŞCĂRII OSCILATORII AMORTIZATE
8
 9.5 Fluxul unui vector printr-o suprafaţă deschisă-continuare Observaţie: Dacă vrem să calculăm fluxul vectorului a = P x y z i + Q x y z j + R x y z k (,, ) (,, ) (,, ) prin suprafaţa definită de ecuaţia
9.5 Fluxul unui vector printr-o suprafaţă deschisă-continuare Observaţie: Dacă vrem să calculăm fluxul vectorului a = P x y z i + Q x y z j + R x y z k (,, ) (,, ) (,, ) prin suprafaţa definită de ecuaţia
C10: Teoria clasică a împrăștierii Considerăm un potențial infinit în interiorul unui domeniu sferic de rază a și o particulă incidentă (Figura 1) la
 C10: Teoria clasică a împrăștierii Considerăm un potențial infinit în interiorul unui domeniu sferic de rază a și o particulă incidentă (Figura 1) la distanta b de centrul sferei. Alegem un sistem de coordonate
C10: Teoria clasică a împrăștierii Considerăm un potențial infinit în interiorul unui domeniu sferic de rază a și o particulă incidentă (Figura 1) la distanta b de centrul sferei. Alegem un sistem de coordonate
Slide 1
 8.4 LAGĂRE Lagărele sunt organe de maşini utilizate la rezemarea şi ghidarea osiilor şi arborilor aflate în mişcare de rotaţie. Clasificarea lagărelor a) în funcţie de direcţia forţei principale care acţionează
8.4 LAGĂRE Lagărele sunt organe de maşini utilizate la rezemarea şi ghidarea osiilor şi arborilor aflate în mişcare de rotaţie. Clasificarea lagărelor a) în funcţie de direcţia forţei principale care acţionează
2
 C5: Metoda matricilor de transfer BIBLIOGRAFIE E. Tulcan Paulescu, M. Paulescu Algorithms for electronic states in artificial semiconductors of use in intermediate band solar cells engineering. In Physics
C5: Metoda matricilor de transfer BIBLIOGRAFIE E. Tulcan Paulescu, M. Paulescu Algorithms for electronic states in artificial semiconductors of use in intermediate band solar cells engineering. In Physics
Ministerul Educa iei i Cercet rii Serviciul Na ional de Evaluare i Examinare EXAMENUL DE BACALAUREAT Proba scris la Fizic Proba E: Specializare
 . MECIC Se consider accelera ia gravita ional g = m/s. Pentru un punct material care se deplaseaz rectiliniu un interval de timp t sub ac iunea unei for e constante F, m rimea fizic egal cu produsul Ft
. MECIC Se consider accelera ia gravita ional g = m/s. Pentru un punct material care se deplaseaz rectiliniu un interval de timp t sub ac iunea unei for e constante F, m rimea fizic egal cu produsul Ft
I
 METODA VECTORIALĂ ÎN GEOMETRIE prof. Andrei - Octavian Dobre Această metodă poate fi descrisă după cum urmează: Fiind dată o problemă de geometrie, după explicitarea şi reprezentarea grafică a configuraţiei
METODA VECTORIALĂ ÎN GEOMETRIE prof. Andrei - Octavian Dobre Această metodă poate fi descrisă după cum urmează: Fiind dată o problemă de geometrie, după explicitarea şi reprezentarea grafică a configuraţiei
Anexa nr. 2 FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituţia de învăţământ superior UNIVERSITATEA DE VEST DIN TIMISOARA 1.2 Facultatea FIZICA 1.
 Anexa nr. 2 FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituţia de învăţământ superior UNIVERSITATEA DE VEST DIN TIMISOARA 1.2 Facultatea FIZICA 1.3 Departamentul FIZICA 1.4 Domeniul de studii FIZICA
Anexa nr. 2 FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituţia de învăţământ superior UNIVERSITATEA DE VEST DIN TIMISOARA 1.2 Facultatea FIZICA 1.3 Departamentul FIZICA 1.4 Domeniul de studii FIZICA
Microsoft Word - Anexa_B.doc
 Anexa B GHID OREINTATIV CU ÎNTREBĂRI PENTRU VERIFICAREA CUNOŞTINŢELOR TEORETICE Cap.1. Noţiuni introductive 1.1. De unde a apărut necesitatea studiului echilibrului şi mişcării fluidelor 1.2. Care sunt
Anexa B GHID OREINTATIV CU ÎNTREBĂRI PENTRU VERIFICAREA CUNOŞTINŢELOR TEORETICE Cap.1. Noţiuni introductive 1.1. De unde a apărut necesitatea studiului echilibrului şi mişcării fluidelor 1.2. Care sunt
DETERMINAREA CONSTANTEI RYDBERG
 UNIVERSITATEA "POLITEHNICA" BUCUREŞTI DEPARTAMENTUL DE FIZICĂ LABORATORUL DE FIZICA ATOMICA SI FIZICA NUCLEARA BN-03 B DETERMINAREA CONSTANTEI RYDBERG DETERMINAREA CONSTANTEI RYDBERG. Scopul lucrării Determinarea
UNIVERSITATEA "POLITEHNICA" BUCUREŞTI DEPARTAMENTUL DE FIZICĂ LABORATORUL DE FIZICA ATOMICA SI FIZICA NUCLEARA BN-03 B DETERMINAREA CONSTANTEI RYDBERG DETERMINAREA CONSTANTEI RYDBERG. Scopul lucrării Determinarea
Fizica fluidelor Cursul 5
 Fizica fluidelor Cursul 5 Victor E. Ambruș Universitatea de Vest din Timișoara Capitolul III. Curgeri potențiale. III.1. Fluidul perfect. III.2. Teorema lui Bernoulli. III.3. Echilibrul hidrostatic. III.4.
Fizica fluidelor Cursul 5 Victor E. Ambruș Universitatea de Vest din Timișoara Capitolul III. Curgeri potențiale. III.1. Fluidul perfect. III.2. Teorema lui Bernoulli. III.3. Echilibrul hidrostatic. III.4.
CURS II Modelarea scurgerii în bazine hidrografice Modelarea scurgerii lichide pe versanţii bazinului hidrografic Modalităţi de cercetare a scurgerii
 CURS II Modelarea scurgerii în bazine hidrografice Modelarea scurgerii lichide pe versanţii bazinului hidrografic Modalităţi de cercetare a scurgerii pe versanţi Versanţii asigură scurgerea apei sub influenţa
CURS II Modelarea scurgerii în bazine hidrografice Modelarea scurgerii lichide pe versanţii bazinului hidrografic Modalităţi de cercetare a scurgerii pe versanţi Versanţii asigură scurgerea apei sub influenţa
Microsoft PowerPoint - SCSEE_10 [Compatibility Mode]
![Microsoft PowerPoint - SCSEE_10 [Compatibility Mode] Microsoft PowerPoint - SCSEE_10 [Compatibility Mode]](/thumbs/102/155245837.jpg) STABILITATEA SI CONTROLUL SISTEMELOR ELECTROENERGETICE Stabilitatea tranzitorie Masuri de imbunatatire Masura de baza: reducerea puterii de accelerare (P 0 P e ) Cum? prin creşterea puterii electromagnetice
STABILITATEA SI CONTROLUL SISTEMELOR ELECTROENERGETICE Stabilitatea tranzitorie Masuri de imbunatatire Masura de baza: reducerea puterii de accelerare (P 0 P e ) Cum? prin creşterea puterii electromagnetice
Clustere şi impurităţi în sisteme complexe
 C: Soluţii numerice ale ecuaţiei Schrödinger independentă de timp. Metoda Tirului BIBLIOGRAFIE Ion. I. Cotaescu. Curs de Mecanica Cuantică, Tipografia UVT 990 Epperson J, An introduction to numerical methods
C: Soluţii numerice ale ecuaţiei Schrödinger independentă de timp. Metoda Tirului BIBLIOGRAFIE Ion. I. Cotaescu. Curs de Mecanica Cuantică, Tipografia UVT 990 Epperson J, An introduction to numerical methods
C2- Energia solara la limita superioara a atmosferei terestre Mişcarea Pământului in jurul Soarelui Mişcarea Pământului în jurul soarelui este o mişca
 C2- Energia solara la limita superioara a atmosferei terestre Mişcarea Pământului in urul Soarelui Mişcarea Pământului în urul soarelui este o mişcare în câmp de forţe centrale. Legile care guverneaă această
C2- Energia solara la limita superioara a atmosferei terestre Mişcarea Pământului in urul Soarelui Mişcarea Pământului în urul soarelui este o mişcare în câmp de forţe centrale. Legile care guverneaă această
Microsoft Word - lucrarea 6
 Materiale avansate / Materiale performante 27 LUCRAREA 6. EXAMINAREA MICROSTRUCTURII MATERIALELOR PRIN MICROSCOPIE OPTICĂ 1. Scopul lucrării. Înțelegerea procedeului de examinare a microstructurii materialelor
Materiale avansate / Materiale performante 27 LUCRAREA 6. EXAMINAREA MICROSTRUCTURII MATERIALELOR PRIN MICROSCOPIE OPTICĂ 1. Scopul lucrării. Înțelegerea procedeului de examinare a microstructurii materialelor
PTO Tractors
 RO F1 70 PTO Tractors RO RO COMISIA COMUNITĂŢILOR EUROPENE Bruxelles, C(2009) Proiect de DIRECTIVĂ../ /CE A COMISIEI din [ ] de modificare, în sensul adaptării la progresul tehnic, a Directivelor 80/720/CEE,
RO F1 70 PTO Tractors RO RO COMISIA COMUNITĂŢILOR EUROPENE Bruxelles, C(2009) Proiect de DIRECTIVĂ../ /CE A COMISIEI din [ ] de modificare, în sensul adaptării la progresul tehnic, a Directivelor 80/720/CEE,
Microsoft Word - Predimensionare_arbori.DOC
 5. PROIECTAREA ARBORILOR - 1 / arbori- Arborii pe care se fixează roţile sunt solicitaţi la: - torsiune de momentele T I, II, III - considerate constante pe fiecare arbore între tronsoanele pe care se
5. PROIECTAREA ARBORILOR - 1 / arbori- Arborii pe care se fixează roţile sunt solicitaţi la: - torsiune de momentele T I, II, III - considerate constante pe fiecare arbore între tronsoanele pe care se
Probleme rezolvate de fizică traducere de Nicolae Coman după lucrarea
 Probleme rezolvate de fizică traducere de Nicolae Coman după lucrarea Contents Vectori... 4 Modul de rezolvare a problemelor... 5 despre vectori... 6 Vector deplasare... 12 Vector viteza... 12 Statica...
Probleme rezolvate de fizică traducere de Nicolae Coman după lucrarea Contents Vectori... 4 Modul de rezolvare a problemelor... 5 despre vectori... 6 Vector deplasare... 12 Vector viteza... 12 Statica...
Cursul 12 (plan de curs) Integrale prime 1 Sisteme diferenţiale autonome. Spaţiul fazelor. Fie Ω R n o mulţime deschisă şi f : Ω R n R n o funcţie de
 Cursul 12 (plan de curs) Integrale prime 1 Sisteme diferenţiale autonome. Spaţiul fazelor. Fie Ω R n o mulţime deschisă şi f : Ω R n R n o funcţie de clasă C 1. Vom considera sistemul diferenţial x = f(x),
Cursul 12 (plan de curs) Integrale prime 1 Sisteme diferenţiale autonome. Spaţiul fazelor. Fie Ω R n o mulţime deschisă şi f : Ω R n R n o funcţie de clasă C 1. Vom considera sistemul diferenţial x = f(x),
E_d_fizica_tehnologic_2019_bar_01_LRO
 Exenul de bacalaueat național 09 Poba E.d) Fizică BAREM DE EALUARE ŞI DE NOTARE aianta Se punctează oicae alte modalităţi de ezolvae coectă a ceinţelo. Nu se acodă facţiuni de punct. Se acodă 0 puncte
Exenul de bacalaueat național 09 Poba E.d) Fizică BAREM DE EALUARE ŞI DE NOTARE aianta Se punctează oicae alte modalităţi de ezolvae coectă a ceinţelo. Nu se acodă facţiuni de punct. Se acodă 0 puncte
CONCURSUL DE MATEMATICǍ ISTEŢII D ARBORE EDIŢIA a X-a - 20 aprilie 2019 Clasa a IV-a BAREM DE CORECTARE ŞI NOTARE SUBIECTUL I Se punctează doar rezult
 CONCURSUL DE MATEMATICǍ ISTEŢII D ARBORE EDIŢIA a X-a - 0 aprilie 09 Clasa a IV-a BAREM DE CORECTARE ŞI NOTARE Se punctează doar rezultatul: pentru fiecare răspuns se acordă fie uncte, fie 0 puncte Nu
CONCURSUL DE MATEMATICǍ ISTEŢII D ARBORE EDIŢIA a X-a - 0 aprilie 09 Clasa a IV-a BAREM DE CORECTARE ŞI NOTARE Se punctează doar rezultatul: pentru fiecare răspuns se acordă fie uncte, fie 0 puncte Nu
CAIET DE LABORATOR PENTRU CLASELE A IX-A ŞI A X-A prof. ELLEN POPOVICI 1
 CAIET DE LABORATOR PENTRU CLASELE A IX-A ŞI A X-A prof. ELLEN POPOVICI 1 ARGUMENT Prin problematica abordată şi modul de structurare a conţinutului, caietul de faţă este destinat deopotrivă elevilor şi
CAIET DE LABORATOR PENTRU CLASELE A IX-A ŞI A X-A prof. ELLEN POPOVICI 1 ARGUMENT Prin problematica abordată şi modul de structurare a conţinutului, caietul de faţă este destinat deopotrivă elevilor şi
Slide 1
 VII. ÎNSCRIEREA PE DESENELE TEHNICE A PRESCRIPŢIILOR DE CALITATE Starea suprafeţelor influenţează fiabilitatea şi funcţionarea pieselor în cadrul unui ansamblu 7.1 STAREA SUPRAFEŢELOR (RUGOZITATEA) SR
VII. ÎNSCRIEREA PE DESENELE TEHNICE A PRESCRIPŢIILOR DE CALITATE Starea suprafeţelor influenţează fiabilitatea şi funcţionarea pieselor în cadrul unui ansamblu 7.1 STAREA SUPRAFEŢELOR (RUGOZITATEA) SR
Universitatea Politehnica din Bucureşti 2019 Disciplina: Geometrie şi Trigonometrie G1 * Varianta A 1. Ştiind cos x = 3 2, atunci sin2 x
 1 5 6 7 Universitatea Politehnica din Bucureşti 019 Disciplina: Geometrie şi Trigonometrie G1 * Varianta A 1 Ştiind cos x atunci sin x este: (6 pct a 1 ; b 1 ; c 1 ; d ; e 1 8 ; f Soluţie Folosind prima
1 5 6 7 Universitatea Politehnica din Bucureşti 019 Disciplina: Geometrie şi Trigonometrie G1 * Varianta A 1 Ştiind cos x atunci sin x este: (6 pct a 1 ; b 1 ; c 1 ; d ; e 1 8 ; f Soluţie Folosind prima
E_d_fizica_teoretic_vocational_2019_bar_model_LRO_2
 Sunt obligatorii toate subiectele din două arii tematice dintre cele patru prevăzute de programă, adică: A. MCANICĂ, B. LMNT D TRMODINAMICĂ, C. PRODUCRA ŞI UTILIZARA CURNTULUI CONTINUU, D. OPTICĂ Se acordă
Sunt obligatorii toate subiectele din două arii tematice dintre cele patru prevăzute de programă, adică: A. MCANICĂ, B. LMNT D TRMODINAMICĂ, C. PRODUCRA ŞI UTILIZARA CURNTULUI CONTINUU, D. OPTICĂ Se acordă
COORDONAT APROBAT Ministerul Educatiei, Culturii Si Cercetirii al Republicii PROGRAM de formare profesionali continui Tipul de formare: Perfectionare
 COORDONAT APROBAT Ministerul Educatiei, Culturii Si Cercetirii al Republicii PROGRAM de formare profesionali continui Tipul de formare: Perfectionare Domeniul: Fizica, Didactica Fizicii qi Astronomi i
COORDONAT APROBAT Ministerul Educatiei, Culturii Si Cercetirii al Republicii PROGRAM de formare profesionali continui Tipul de formare: Perfectionare Domeniul: Fizica, Didactica Fizicii qi Astronomi i
Microsoft Word - C05_Traductoare de deplasare de tip transformator
 Traductoare de deplasare de tip transformator Traductoare parametrice. Principiul de funcţionare: Modificarea inductivităţii mutuale a unor bobine cu întrefier variabil sau constant. Ecuaţia care exprimă
Traductoare de deplasare de tip transformator Traductoare parametrice. Principiul de funcţionare: Modificarea inductivităţii mutuale a unor bobine cu întrefier variabil sau constant. Ecuaţia care exprimă
Ministerul Educa iei i Cercet rii Serviciul Na ional de Evaluare i Examinare EXAMENUL DE BACALAUREAT Proba scris la Fizic Proba E: Specializare
 A. MECANIC Se consider accelera ia gravita ional g = m/s.. p inând cont c nota iile sunt cele utilizate în manuale de fizic, reprezint : t a. for a medie b. accelera ia medie c. viteza medie d. puterea
A. MECANIC Se consider accelera ia gravita ional g = m/s.. p inând cont c nota iile sunt cele utilizate în manuale de fizic, reprezint : t a. for a medie b. accelera ia medie c. viteza medie d. puterea
Ministerul Educa iei i Cercet rii Serviciul Na ional de Evaluare i Examinare EXAMENUL DE BACALAUREAT Proba scris la Fizic Proba E: Specializare
 MECNIC Se consider accelera ia gravita ional g = 0 / s inând cont c nota iile sunt cele utilizate în anualele de fizic, teorea varia iei energiei cinetice pentru un punct aterial are expresia: a L = EC
MECNIC Se consider accelera ia gravita ional g = 0 / s inând cont c nota iile sunt cele utilizate în anualele de fizic, teorea varia iei energiei cinetice pentru un punct aterial are expresia: a L = EC
ROBOT DRSTINAT STINGERII INCENDIILOR
 ROBOT DESTINAT STINGERII INCENDIILOR ÎN MEDII OSTILE OMULUI Lect.univ.drd.ing. Ştefan TRACHE Prof.dr.ing. Ioan FLUCUŞ Conf.dr.ing. Dan CAVAROPOL Academia de Poliţie Aleandru Ioan Cuza Facultatea de Pompieri
ROBOT DESTINAT STINGERII INCENDIILOR ÎN MEDII OSTILE OMULUI Lect.univ.drd.ing. Ştefan TRACHE Prof.dr.ing. Ioan FLUCUŞ Conf.dr.ing. Dan CAVAROPOL Academia de Poliţie Aleandru Ioan Cuza Facultatea de Pompieri
Subiecte
 Cap. Semnale şi instrumente pentru generarea lor. Ce tipuri de aparate pot genera semnal sinusoidal? 2. Care sunt principalele caracteristici ale unui generator de audio frecvenţă? 3. Care sunt principalele
Cap. Semnale şi instrumente pentru generarea lor. Ce tipuri de aparate pot genera semnal sinusoidal? 2. Care sunt principalele caracteristici ale unui generator de audio frecvenţă? 3. Care sunt principalele
PROGRAMA CONCURSULUI NAŢIONAL
 ANUL ŞCOLAR 2011-2012 CLASA a IX-a În programa de concurs pentru clasa a IX-a sunt incluse conţinuturile programelor din clasele anterioare şi din etapele anterioare. 1. Mulţimi şi elemente de logică matematică.
ANUL ŞCOLAR 2011-2012 CLASA a IX-a În programa de concurs pentru clasa a IX-a sunt incluse conţinuturile programelor din clasele anterioare şi din etapele anterioare. 1. Mulţimi şi elemente de logică matematică.
CERCURI REMARCABILE ASOCIATE UNUI TRIUNGHI CERCURI EXÎNSCRISE Natura vorbeşte în limbajul matematicii: literele acestei limbi sunt cercuri, tri
 CERCURI REMARCABILE ASOCIATE UNUI TRIUNGHI 19 3. CERCURI EXÎNSCRISE Natura vorbeşte în limbajul matematicii: literele acestei limbi sunt cercuri, triunghiuri şi alte guri geometrice. Galileo Galilei 3
CERCURI REMARCABILE ASOCIATE UNUI TRIUNGHI 19 3. CERCURI EXÎNSCRISE Natura vorbeşte în limbajul matematicii: literele acestei limbi sunt cercuri, triunghiuri şi alte guri geometrice. Galileo Galilei 3
Microsoft Word - Matematika_kozep_irasbeli_javitasi_0911_roman.doc
 Matematika román nyelven középszint 0911 ÉRETTSÉGI VIZSGA 011. május. MATEMATIKA ROMÁN NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ NEMZETI ERŐFORRÁS MINISZTÉRIUM Indicaţii
Matematika román nyelven középszint 0911 ÉRETTSÉGI VIZSGA 011. május. MATEMATIKA ROMÁN NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ NEMZETI ERŐFORRÁS MINISZTÉRIUM Indicaţii
fc 1 distribuitoare hidraulice dn6.cdr
 1 50 l/min 315 bar Distribuitoare hidraulice Dn 6 GENERALITATI FC - 1 Distribuitoare cu sertar cu 4 orificii si 2 sau 3 pozitii de lucru (4/2 sau 2/3) Comanda directa realizata : manual, cu maneta mecanic,
1 50 l/min 315 bar Distribuitoare hidraulice Dn 6 GENERALITATI FC - 1 Distribuitoare cu sertar cu 4 orificii si 2 sau 3 pozitii de lucru (4/2 sau 2/3) Comanda directa realizata : manual, cu maneta mecanic,
DAN LASCU ADRIANA-LIGIA SPORIŞ ANDA OLTEANU PAUL VASILIU MATEMATICĂ. CULEGERE DE PROBLEME TIP GRILĂ PENTRU ADMITEREA ÎN ACADEMIA NAVALĂ MIRCEA CEL BĂT
 DAN LASCU ADRIANA-LIGIA SPORIŞ ANDA OLTEANU PAUL VASILIU MATEMATICĂ. CULEGERE DE PROBLEME TIP GRILĂ PENTRU ADMITEREA ÎN ACADEMIA NAVALĂ MIRCEA CEL BĂTRÂN Colecţia Matematică DAN LASCU ADRIANA-LIGIA SPORIŞ
DAN LASCU ADRIANA-LIGIA SPORIŞ ANDA OLTEANU PAUL VASILIU MATEMATICĂ. CULEGERE DE PROBLEME TIP GRILĂ PENTRU ADMITEREA ÎN ACADEMIA NAVALĂ MIRCEA CEL BĂTRÂN Colecţia Matematică DAN LASCU ADRIANA-LIGIA SPORIŞ
OptiFlood LED BVP506 |
 Lighting OptiFlood LED tot ce este necesar pentru iluminatul perimetrelor OptiFlood LED este o gamă de reflectoare elegante, deosebit de eficiente, asimetrice, care pot fi utilizate pentru a ilumina zone
Lighting OptiFlood LED tot ce este necesar pentru iluminatul perimetrelor OptiFlood LED este o gamă de reflectoare elegante, deosebit de eficiente, asimetrice, care pot fi utilizate pentru a ilumina zone
Pachete de lecţii disponibile pentru platforma AeL
 Pachete de lecţii disponibile pentru platforma AeL -disciplina Matematică- Nr. crt Nume pachet clasa Nr. momente Nr.Recomandat de ore 1 Corpuri geometrice V 6 1 2 Fracţii V 14 5 3 Măsurarea lungimilor.
Pachete de lecţii disponibile pentru platforma AeL -disciplina Matematică- Nr. crt Nume pachet clasa Nr. momente Nr.Recomandat de ore 1 Corpuri geometrice V 6 1 2 Fracţii V 14 5 3 Măsurarea lungimilor.
Slide 1
 ELECTROTEHNICĂ ET A I - IA CUR 6 Cof.dr.ig.ec. Claudia PĂCURAR e-mail: Claudia.Pacurar@ethm.utcluj.ro . Legea iducției electromagetice 2. Eergii și forțe î câmp magetic . Legea iducției electromagetice
ELECTROTEHNICĂ ET A I - IA CUR 6 Cof.dr.ig.ec. Claudia PĂCURAR e-mail: Claudia.Pacurar@ethm.utcluj.ro . Legea iducției electromagetice 2. Eergii și forțe î câmp magetic . Legea iducției electromagetice
Nr. 644/ , Ediția Nr. 2, 1/5 Corp de iluminat protejat la praf și umezeală CALYPSO-02 LED CALYPSO-02 D LED 4000K PCOP, CALYPSO-02 D335
 Nr. 644/ 10.06.2014, Ediția Nr. 2, 1/5 Corp de iluminat protejat la praf și umezeală CALYPSO-02 LED CALYPSO-02 D335 63 LED 4000K PCOP, CALYPSO-02 D335 63 LED 4000K PCTS PCOP PCTS Despre produs Calypso
Nr. 644/ 10.06.2014, Ediția Nr. 2, 1/5 Corp de iluminat protejat la praf și umezeală CALYPSO-02 LED CALYPSO-02 D335 63 LED 4000K PCOP, CALYPSO-02 D335 63 LED 4000K PCTS PCOP PCTS Despre produs Calypso
COMENTARII FAZA JUDEŢEANĂ, 9 MARTIE 2013 Abstract. Personal comments on some of the problems presented at the District Round of the National Mathemati
 COMENTARII FAZA JUDEŢEANĂ, 9 MARTIE 2013 Abstract. Personal comments on some of the problems presented at the District Round of the National Mathematics Olympiad 2013. Data: 12 martie 2013. Autor: Dan
COMENTARII FAZA JUDEŢEANĂ, 9 MARTIE 2013 Abstract. Personal comments on some of the problems presented at the District Round of the National Mathematics Olympiad 2013. Data: 12 martie 2013. Autor: Dan
Enter Title Here
 FORȚA CAPACITATE MOTRICĂ DE BAZĂ A ARBITRULUI DE FOTBAL -ARBITRII AR TREBUI SA FIE: În forma din punct de vedere fizic, puternici, rezistenti la accidentari si cu un aspect atletic - De-a lungul anilor
FORȚA CAPACITATE MOTRICĂ DE BAZĂ A ARBITRULUI DE FOTBAL -ARBITRII AR TREBUI SA FIE: În forma din punct de vedere fizic, puternici, rezistenti la accidentari si cu un aspect atletic - De-a lungul anilor
Ceea ce este în interior face diferența
 PHILIPS LED Spot (Putere reglabilă) 4 W (35 W) GU10 Alb rece Intensitate luminoasă reglabilă Ceea ce este în interior face diferența Cu forma sa frumoasă și dimensiunile familiare, acest spot cu LED este
PHILIPS LED Spot (Putere reglabilă) 4 W (35 W) GU10 Alb rece Intensitate luminoasă reglabilă Ceea ce este în interior face diferența Cu forma sa frumoasă și dimensiunile familiare, acest spot cu LED este
Alimentatoare AX-3003D, AX-3005D AX-1803D Instrucţiuni de utilizare
 Alimentatoare AX-3003D, AX-3005D AX-1803D Instrucţiuni de utilizare Cuprins 1. Introducere... 3 Despachetarea şi verificarea componenţei setului... 3 Indicaţii privind siurana... 4 Informaţii privind siurana...
Alimentatoare AX-3003D, AX-3005D AX-1803D Instrucţiuni de utilizare Cuprins 1. Introducere... 3 Despachetarea şi verificarea componenţei setului... 3 Indicaţii privind siurana... 4 Informaţii privind siurana...
Microsoft Word - Programa finala olimpiadei matematica 2007 gimnaziu.doc
 ROMÂNIA MINISTERUL EDUCAŢIEI ŞI CERCETĂRII DIRECŢIA GENERALĂ ÎNVĂŢĂMÂNT PREUNIVERSITAR SERVICIUL NAŢIONAL DE EVALUARE ŞI EXAMINARE PROGRAMA OLIMPIADEI DE MATEMATICĂ CLASELE V XII AN ŞCOLAR 006 / 007 Pentru
ROMÂNIA MINISTERUL EDUCAŢIEI ŞI CERCETĂRII DIRECŢIA GENERALĂ ÎNVĂŢĂMÂNT PREUNIVERSITAR SERVICIUL NAŢIONAL DE EVALUARE ŞI EXAMINARE PROGRAMA OLIMPIADEI DE MATEMATICĂ CLASELE V XII AN ŞCOLAR 006 / 007 Pentru
CONCURSUL DE MATEMATICĂ APLICATĂ "ADOLF HAIMOVICI" ETAPA JUDEȚEANĂ 18 martie 2017 Filiera Tehnologică : profilul Tehnic Clasa a IX -a Problema 1. 2 Se
 Clasa a IX -a Se consideră funcţia f : R R, f ( x) x mx 07, unde mr a) Determinaţi valoarea lui m ştiind că f( ), f() şi f () sunt termeni consecutivi ai unei progresii aritmetice b) Dacă f() f(4), să
Clasa a IX -a Se consideră funcţia f : R R, f ( x) x mx 07, unde mr a) Determinaţi valoarea lui m ştiind că f( ), f() şi f () sunt termeni consecutivi ai unei progresii aritmetice b) Dacă f() f(4), să
RecMat dvi
 Conice şi cubice în probleme elementare de loc geometric Ştefan DOMINTE 1 Abstract. In this Note, a number of simple problems are presented to support the idea that conic and cubic curves can frequently
Conice şi cubice în probleme elementare de loc geometric Ştefan DOMINTE 1 Abstract. In this Note, a number of simple problems are presented to support the idea that conic and cubic curves can frequently
Subiecte_funar_2006.doc
 Clasa a VIII-a A. 1. Exista numere n Z astfel încât n si n+ sa fie patrate perfecte? (Gheorghe Stoica) A. 2. Se considera A N o multime cu 7 elemente si k N*. Aratati ca ecuatia 4x 2 4ax+b 2 +10k = 0,
Clasa a VIII-a A. 1. Exista numere n Z astfel încât n si n+ sa fie patrate perfecte? (Gheorghe Stoica) A. 2. Se considera A N o multime cu 7 elemente si k N*. Aratati ca ecuatia 4x 2 4ax+b 2 +10k = 0,
Microsoft Word - Concursul SFERA.doc
 CONCURSUL INTERJUDEŢEAN DE MATEMATICĂ SFERA EDIŢIA a II-a BĂILEŞTI, 1 martie 005 CLASA a IV-a Pentru întrebările 1-5 scrieţi pe lucrare litera corespunzătoare răspunsului corect 1. Care este numărul care
CONCURSUL INTERJUDEŢEAN DE MATEMATICĂ SFERA EDIŢIA a II-a BĂILEŞTI, 1 martie 005 CLASA a IV-a Pentru întrebările 1-5 scrieţi pe lucrare litera corespunzătoare răspunsului corect 1. Care este numărul care
Olimpiada de Astronomie şi Astrofizică Etapa Naţională 2015 Proba de Baraj Juniori Problema 1 O tehnică de determinare a magnitudinii stelelor o const
 Problema O tehnică e eterminare a magnituinii stelelor o constituie analiza fotometrică a imaginilor înregistrate pe o placă fotografică sau cu ajutorul unei matrici e fotoetectori. Figura reprezintă o
Problema O tehnică e eterminare a magnituinii stelelor o constituie analiza fotometrică a imaginilor înregistrate pe o placă fotografică sau cu ajutorul unei matrici e fotoetectori. Figura reprezintă o
Microsoft Word - Rezolvarea Test nr. 11.doc
 Testul nr. 11 Problema 1 (30 puncte = 10 puncte + 10 puncte + 10 puncte) a) Să se calculeze ( 42 : 2 + 23 ) :11+ 2 5 16. b) Să se determine cifrele a și b din egalitatea { a b} 2 + 42 : 2 + 23 :11+ 2 5
Testul nr. 11 Problema 1 (30 puncte = 10 puncte + 10 puncte + 10 puncte) a) Să se calculeze ( 42 : 2 + 23 ) :11+ 2 5 16. b) Să se determine cifrele a și b din egalitatea { a b} 2 + 42 : 2 + 23 :11+ 2 5
CURRICULUM VITAE
 8.4. Calculul stabilizatorului 1 Schema stabilizatorului 1 este prezentată în figura 8.7. Fig. 8.7. Schema stabilizatorului 1, cu diodă zener şi tranzistor Date de pornire pentru stabilizatorul 1: U 1
8.4. Calculul stabilizatorului 1 Schema stabilizatorului 1 este prezentată în figura 8.7. Fig. 8.7. Schema stabilizatorului 1, cu diodă zener şi tranzistor Date de pornire pentru stabilizatorul 1: U 1
2
 C4: Structuri nanocristaline. Modelul Kronig-Penney 1. Stucturi cuantice traditionale Reducerea dimensionalităţii unui sistem fizic (de exemplu material semiconductor) produsă prin confinarea particulelor
C4: Structuri nanocristaline. Modelul Kronig-Penney 1. Stucturi cuantice traditionale Reducerea dimensionalităţii unui sistem fizic (de exemplu material semiconductor) produsă prin confinarea particulelor
STCD_1.pdf
 3. PROIECTAREA SISTEMULUI DE TRANSMITERE PRIN CUREA DIN AT Acest tip constructiv de sistem de transmitere func ionez prin angrenarea din ilor curelei cu din ii ro ilor de curea, iar metodica de calcul
3. PROIECTAREA SISTEMULUI DE TRANSMITERE PRIN CUREA DIN AT Acest tip constructiv de sistem de transmitere func ionez prin angrenarea din ilor curelei cu din ii ro ilor de curea, iar metodica de calcul
Microsoft Word - 11_2016_OJF_barem.doc
 Pagina din 9 Subiect. ortizare cu frecare la alunecare Parţial Punctaj ubiect 0 a.,5 d x i) Ecuația ișcării ete: +x = 0. () ceată ecuație are oluții de fora x ( t) = co( ω t +ϕ0 ). Legea vitezei ete v
Pagina din 9 Subiect. ortizare cu frecare la alunecare Parţial Punctaj ubiect 0 a.,5 d x i) Ecuația ișcării ete: +x = 0. () ceată ecuație are oluții de fora x ( t) = co( ω t +ϕ0 ). Legea vitezei ete v
Catalog Solentis Refacere sept rev
 www.solentis.ro Șos. Alexandriei nr. 76-78, Bragadiru Ilfov Solentis este un brand care a luat naștere în urma nevoilor și a cerințelor din ce în ce mai elaborate și mai complexe ale pieței din România.
www.solentis.ro Șos. Alexandriei nr. 76-78, Bragadiru Ilfov Solentis este un brand care a luat naștere în urma nevoilor și a cerințelor din ce în ce mai elaborate și mai complexe ale pieței din România.
Microsoft Word - Coperta-Cuprins-Prefata.doc
 Universitatea TRANSILVANIA din Braşov GEORGE NICOLAE IOAN D. OLTEAN RADIOCOMUNICAŢII BAZELE COMUNICAŢIILOR PRIN RADIO ŞI TELEVIZIUNE Volumul 1 TV - 2000 - UNIVERSITATEA TRANSILVANIA BRAŞOV FACULTATEA DE
Universitatea TRANSILVANIA din Braşov GEORGE NICOLAE IOAN D. OLTEAN RADIOCOMUNICAŢII BAZELE COMUNICAŢIILOR PRIN RADIO ŞI TELEVIZIUNE Volumul 1 TV - 2000 - UNIVERSITATEA TRANSILVANIA BRAŞOV FACULTATEA DE
Olimpiada Națională de Astronomie şi Astrofizică Aprilie 2019 Analiza Datelor - Seniori Problema 1 - Quasar 3C273 Spectrul optic al quasarului 3C273 c
 Problema - Quasar 3C273 Spectrul optic al quasarului 3C273 conține liniile spectrale ale hidrogenului. Se cunosc lungimile de undă ale hidrogenului, obținute în condiții de laborator: Hα = 656,3 nm; Hβ
Problema - Quasar 3C273 Spectrul optic al quasarului 3C273 conține liniile spectrale ale hidrogenului. Se cunosc lungimile de undă ale hidrogenului, obținute în condiții de laborator: Hα = 656,3 nm; Hβ
E_d_fizica_teoretic_vocational_2015_bar_09_LRO
 Proba E. d) Sunt obligatorii toate subiectele din două arii tematice dintre cele patru prevăzute de programă, adică: A. MECANICĂ, B. ELEMENTE DE TERMODINAMICĂ, C. PRODUCEREA ŞI UTILIZAREA CURENTULUI CONTINUU,
Proba E. d) Sunt obligatorii toate subiectele din două arii tematice dintre cele patru prevăzute de programă, adică: A. MECANICĂ, B. ELEMENTE DE TERMODINAMICĂ, C. PRODUCEREA ŞI UTILIZAREA CURENTULUI CONTINUU,
Microsoft Word - CURSURI introductiv macanica 16-17
 CAP II. PRINCIPII ŞI LEGI ALE MECANICII. Au fost enunţate de către fizicianul Isaac Newton în cartea sa: Principiile matematice ale filozofiei naturii în anul 1867 şi au constituit trecerea fizicii din
CAP II. PRINCIPII ŞI LEGI ALE MECANICII. Au fost enunţate de către fizicianul Isaac Newton în cartea sa: Principiile matematice ale filozofiei naturii în anul 1867 şi au constituit trecerea fizicii din
Doina BOAZU
 Doina BOAZU REZISTENŢA MATERIALELOR Solicitările simple şi compuse ale barelor EDITURA EUROPLUS GALAŢI PREFAŢĂ Această carte conţine structura de bază a cursului de Rezistenţa materialelor predat studenţilor
Doina BOAZU REZISTENŢA MATERIALELOR Solicitările simple şi compuse ale barelor EDITURA EUROPLUS GALAŢI PREFAŢĂ Această carte conţine structura de bază a cursului de Rezistenţa materialelor predat studenţilor
Soft Easy Hard IMPLANTURI
 Soft Easy Hard IMPLANTURI Soft... Implant Spirală Suprafață anodică antibacteriană Implantul SOFT auto-forant este un produs unic, bazat pe un design tradițional și îmbunătățit prin forma spirelor de la
Soft Easy Hard IMPLANTURI Soft... Implant Spirală Suprafață anodică antibacteriană Implantul SOFT auto-forant este un produs unic, bazat pe un design tradițional și îmbunătățit prin forma spirelor de la
A TANTÁRGY ADATLAPJA
 FIȘA DISCIPLINEI 1. Date despre program 1.1. Instituția de învățământ superior Universitatea Sapientia din Cluj-Napoca 1.2. Facultatea Științe Tehnice și Umaniste din Târgu-Mureș 1.3. Domeniul de studii
FIȘA DISCIPLINEI 1. Date despre program 1.1. Instituția de învățământ superior Universitatea Sapientia din Cluj-Napoca 1.2. Facultatea Științe Tehnice și Umaniste din Târgu-Mureș 1.3. Domeniul de studii
Gheorghe IUREA Adrian ZANOSCHI algebră geometrie clasa a VII-a ediţia a V-a, revizuită mate 2000 standard EDITURA PARALELA 45 Matematică. Clasa a VII-
 Gheorghe IUREA Adrian ZANOSCHI algebră geometrie clasa a VII-a ediţia a V-a, revizuită mate 2000 standard 3 Algebră Capitolul I. MULŢIMEA NUMERELOR RAŢIONALE Identificarea caracteristicilor numerelor raţionale
Gheorghe IUREA Adrian ZANOSCHI algebră geometrie clasa a VII-a ediţia a V-a, revizuită mate 2000 standard 3 Algebră Capitolul I. MULŢIMEA NUMERELOR RAŢIONALE Identificarea caracteristicilor numerelor raţionale
Microsoft Word - Programa_Evaluare_Nationala_2011_Matematica.doc
 C E N T R U L NAłIONAL DE EVALUARE ŞI E X A M I N A R E PROGRAMA PENTRU DISCIPLINA MATEMATICĂ EVALUAREA NAłIONALĂ PENTRU ELEVII CLASEI A VIII A Pagina 1 din 5 PROGRAMA PENTRU DISCIPLINA MATEMATICĂ I. STATUTUL
C E N T R U L NAłIONAL DE EVALUARE ŞI E X A M I N A R E PROGRAMA PENTRU DISCIPLINA MATEMATICĂ EVALUAREA NAłIONALĂ PENTRU ELEVII CLASEI A VIII A Pagina 1 din 5 PROGRAMA PENTRU DISCIPLINA MATEMATICĂ I. STATUTUL
Microsoft Word - mem pud
 PLAN URBANISTIC DETALIU DESFIINTARE CONSTRUCTII EXISTENTE CONSTRUIRE SHOW ROOM TEXTILE IMPREMUIRE STR PLOPILOR 18 BACĂU BENEFICIAR: - SC ANCA-ROM SRL 1 SC REAL PROIECT CONSTRUCT SRL L I S T Ă D E S E M
PLAN URBANISTIC DETALIU DESFIINTARE CONSTRUCTII EXISTENTE CONSTRUIRE SHOW ROOM TEXTILE IMPREMUIRE STR PLOPILOR 18 BACĂU BENEFICIAR: - SC ANCA-ROM SRL 1 SC REAL PROIECT CONSTRUCT SRL L I S T Ă D E S E M
ENVI_2018_matematica_si_stiinte_Test_1_Caietul_elevului_Limba_romana
 EVALUAREA NAŢIONALĂ LA FINALUL CLASEI a VI-a Anul școlar 2017-2018 Matematică şi Ştiinţe ale naturii TEST 1 Judeţul/sectorul... Localitatea... Unitatea de învățământ... Numele şi prenumele elevei/elevului......
EVALUAREA NAŢIONALĂ LA FINALUL CLASEI a VI-a Anul școlar 2017-2018 Matematică şi Ştiinţe ale naturii TEST 1 Judeţul/sectorul... Localitatea... Unitatea de învățământ... Numele şi prenumele elevei/elevului......
Teoreme cu nume 1. Problema (Năstăsescu IX, p 147, propoziţia 5) Formula lui Chasles Pentru orice puncte M, N şi P avem MN + NP = MP.
 Teoreme cu nume Problema (Năstăsescu IX, p 47, propoziţia 5) Formula lui hasles Pentru orice puncte M, N şi P avem MN + NP = MP 2 Problema (Năstăsescu IX, p 68, teoremă) Vectorul de poziţie al centrului
Teoreme cu nume Problema (Năstăsescu IX, p 47, propoziţia 5) Formula lui hasles Pentru orice puncte M, N şi P avem MN + NP = MP 2 Problema (Năstăsescu IX, p 68, teoremă) Vectorul de poziţie al centrului
carteInvataturaEd_2.0_lectia5.pdf
 Lect ia3 Diagrame Veitch-Karnaugh 5.1 Noţiuni teoretice Diagramele Veich-Karnaugh (V-K) sunt o modalitate de reprezentare grafică a funcţiilor logice. Pentru o funct ie de N variabile, diagrama corespunz
Lect ia3 Diagrame Veitch-Karnaugh 5.1 Noţiuni teoretice Diagramele Veich-Karnaugh (V-K) sunt o modalitate de reprezentare grafică a funcţiilor logice. Pentru o funct ie de N variabile, diagrama corespunz
ANEXA nr
 FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituţia de învăţământ superior Universitatea Tehnică din Cluj-Napoca 1. Facultatea de Inginerie 1.3 Departamentul de Inginerie Electrică, Electronică și Calculatoare
FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituţia de învăţământ superior Universitatea Tehnică din Cluj-Napoca 1. Facultatea de Inginerie 1.3 Departamentul de Inginerie Electrică, Electronică și Calculatoare
Student: Mădălina-Maria Mitricioaei Titlul proiectului: IOT Sensor Hub Rezumat
 Student: Mădălina-Maria Mitricioaei Email: madalina.mitricioaei@outlook.com, madalina.mitricioaei@gmail.com Titlul proiectului: IOT Sensor Hub Rezumat Proiectul de față are ca scop dezvoltarea unei sistem
Student: Mădălina-Maria Mitricioaei Email: madalina.mitricioaei@outlook.com, madalina.mitricioaei@gmail.com Titlul proiectului: IOT Sensor Hub Rezumat Proiectul de față are ca scop dezvoltarea unei sistem
A.E.F. - suport laborator nr.1 sem.ii Noțiuni generale pentru analiza cu elemente finite utilizând Siemens NX Nastran (1) În acest laborator sunt atin
 Noțiuni generale pentru analiza cu elemente finite utilizând Siemens NX Nastran (1) În acest laborator sunt atinse următoarele aspecte: termeni și concepte uzuale din analiza cu elemente finite, noțiuni
Noțiuni generale pentru analiza cu elemente finite utilizând Siemens NX Nastran (1) În acest laborator sunt atinse următoarele aspecte: termeni și concepte uzuale din analiza cu elemente finite, noțiuni
Antet stanga Beneficiar: Executant: Proiectant: Obiectivul: Obiectul: Stadiul fizic: Corkline 01 Corkline 01 Corkline edevize Anexa explicitare norme
 Beneficiar: Executant: Proiectant: Obiectivul: Obiectul: Stadiul fizic: Corkline 01 Corkline 01 Corkline Anexa explicitare norme IZF9A01^ mm, conductivitatea termica de 0,00 W/mK, pe suprafete orizontale
Beneficiar: Executant: Proiectant: Obiectivul: Obiectul: Stadiul fizic: Corkline 01 Corkline 01 Corkline Anexa explicitare norme IZF9A01^ mm, conductivitatea termica de 0,00 W/mK, pe suprafete orizontale
MENGHINA MECANICĂ tip MM - 125
 MENGHINA MECANICĂ tip MM - 125 2 1 Descriere Menghina mecanică pentru mașinile de frezat cu comandă numerică şi nu numai, NGV.MM-125, produsă de NOVA GRUP, este recomandată atât pentru producţia de serie
MENGHINA MECANICĂ tip MM - 125 2 1 Descriere Menghina mecanică pentru mașinile de frezat cu comandă numerică şi nu numai, NGV.MM-125, produsă de NOVA GRUP, este recomandată atât pentru producţia de serie
CONCURSUL NAŢIONAL DE MATEMATICA PANAITOPOL EDIŢIA a X-a, TULCEA, 21 aprilie 2018 Clasa a VII - a 1. Se consideră numerele reale x, y şi z, cel puţin
 CONCURSUL NAŢIONAL DE MATEMATICA PANAITOPOL EDIŢIA a X-a, TULCEA, 21 aprilie 2018 Clasa a VII - a 1. Se consideră numerele reale x, y şi z, cel puţin două dintre ele fiind diferite. Arătaţi că x y z 0
CONCURSUL NAŢIONAL DE MATEMATICA PANAITOPOL EDIŢIA a X-a, TULCEA, 21 aprilie 2018 Clasa a VII - a 1. Se consideră numerele reale x, y şi z, cel puţin două dintre ele fiind diferite. Arătaţi că x y z 0
Coordonate baricentrice Considerăm în plan un triunghi ABC şi un punct Q în interiorul său, fixat arbitrar. Notăm σ c = aria ( QAB) σ a = aria ( QBC),
 Coordonate baricentrice Considerăm în plan un triunghi ABC şi un punct Q în interiorul său, fixat arbitrar Notăm σ c = aria ( QAB) = aria ( QBC), = aria ( QCA) şi σ = aria ( ABC), astfel încât σ = + +
Coordonate baricentrice Considerăm în plan un triunghi ABC şi un punct Q în interiorul său, fixat arbitrar Notăm σ c = aria ( QAB) = aria ( QBC), = aria ( QCA) şi σ = aria ( ABC), astfel încât σ = + +
11 ACO Spin Rigole și Guri de scurgere pentru terase Guri de scurgere telescopice ACO Spin fără sifonare - DN 70/ DN100 Rigole Guri de scurgere telesc
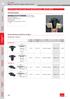 telescopice fără sifonare - DN 70/ DN100 telescopice fără sifonare - DN 70/ DN100 Informații produs Avantaje produs Testat conform SR EN 1253 vopsită Rezistență la presiune ridicată >700 N/ mm² Fără sifonare
telescopice fără sifonare - DN 70/ DN100 telescopice fără sifonare - DN 70/ DN100 Informații produs Avantaje produs Testat conform SR EN 1253 vopsită Rezistență la presiune ridicată >700 N/ mm² Fără sifonare
_DE0735_RO.indd
 402114-78 RO Traducere a instrucţiunilor originale DE0735 1 2 3 4 5 A 2 6 B 7 C 1 12 10 11 9 D 5 8 E 3 13 F 4 TREPIED DE0735 Felicitări! Aţi ales un produs DEWALT. Anii de experienţă, cercetarea şi inovarea
402114-78 RO Traducere a instrucţiunilor originale DE0735 1 2 3 4 5 A 2 6 B 7 C 1 12 10 11 9 D 5 8 E 3 13 F 4 TREPIED DE0735 Felicitări! Aţi ales un produs DEWALT. Anii de experienţă, cercetarea şi inovarea
Algebra si Geometri pentru Computer Science
 Natura este scrisă în limbaj matematic. Galileo Galilei 5 Aplicatii liniare Grafica vectoriala In grafica pe calculator, grafica vectoriala este un procedeu prin care imaginile sunt construite cu ajutorul
Natura este scrisă în limbaj matematic. Galileo Galilei 5 Aplicatii liniare Grafica vectoriala In grafica pe calculator, grafica vectoriala este un procedeu prin care imaginile sunt construite cu ajutorul
Nr. 788/ , Ediția Nr. 7, 1/5 INFORMATIVĂ Corp de iluminat stradal și rezidențial PRIME LED PRIME-01 6LED, PRIME-01 12LED Despre produs Produ
 Nr. 788/ 21.06.2017, Ediția Nr. 7, 1/5 Corp de iluminat stradal și rezidențial PRIME LED PRIME-01 6LED, PRIME-01 12LED Despre produs Produsul PRIME LED este varianta optimă echipată cu module LED de ultimă
Nr. 788/ 21.06.2017, Ediția Nr. 7, 1/5 Corp de iluminat stradal și rezidențial PRIME LED PRIME-01 6LED, PRIME-01 12LED Despre produs Produsul PRIME LED este varianta optimă echipată cu module LED de ultimă
Problema 1
 Olimpiada Nationala de Astronomie 1-2 Mai 2003 Problema 1 Corpul omenesc are o serie de segmente care pot fi folosite la determinarea unghiurilor intre diferite obiecte pe bolta cereasca. Figura 2 Figura
Olimpiada Nationala de Astronomie 1-2 Mai 2003 Problema 1 Corpul omenesc are o serie de segmente care pot fi folosite la determinarea unghiurilor intre diferite obiecte pe bolta cereasca. Figura 2 Figura
Slide 1
 ELECTROTEHNCĂ ET An - SA CRS 8 Conf.dr.ing.ec. Claudia PĂCRAR e-mail: Claudia.Pacurar@ethm.utcluj.ro . ntroducere în teoria circuitelor electrice. Puteri în regim armonic 3. Caracterizarea în complex a
ELECTROTEHNCĂ ET An - SA CRS 8 Conf.dr.ing.ec. Claudia PĂCRAR e-mail: Claudia.Pacurar@ethm.utcluj.ro . ntroducere în teoria circuitelor electrice. Puteri în regim armonic 3. Caracterizarea în complex a
TEMA 4 Îndrumar de proiectare Fundații Asist.dr.ing. Florin BEJAN Proiectarea fundațiilor de suprafață izolate 4.1. Tema de proiectare Pe am
 TEMA 4 Proiectarea fundațiilor de suprafață izolate 4.1. Tema de proiectare Pe amplasamentul caracterizat prin profilul forajului F2 este prevăzută realizarea unui construcții industriale încadrată în
TEMA 4 Proiectarea fundațiilor de suprafață izolate 4.1. Tema de proiectare Pe amplasamentul caracterizat prin profilul forajului F2 este prevăzută realizarea unui construcții industriale încadrată în
Studiul de fezabilitate a implementării iluminatului public eficient pe strada Vasile Alecsandri or. Cimişlia eficienta energetică
 Studiul de fezabilitate a implementării iluminatului public eficient pe strada Vasile Alecsandri or. Cimişlia eficienta Introducere Iluminatul căilor de circulaţie rutieră, cel mai important din cadrul
Studiul de fezabilitate a implementării iluminatului public eficient pe strada Vasile Alecsandri or. Cimişlia eficienta Introducere Iluminatul căilor de circulaţie rutieră, cel mai important din cadrul
Universitatea Lucian Blaga din Sibiu Facultatea de Inginerie Departamentul de Calculatoare şi Inginerie Electrică FIŞA DISCIPLINEI * Valabil an univer
 FIŞA DISCIPLINEI * Valabil an universitar 2018-2019 1. Date despre program Instituţia de învăţământ superior Facultatea Departament Domeniul de studiu Ciclul de studii Specializarea Universitatea Lucian
FIŞA DISCIPLINEI * Valabil an universitar 2018-2019 1. Date despre program Instituţia de învăţământ superior Facultatea Departament Domeniul de studiu Ciclul de studii Specializarea Universitatea Lucian
CONCURSUL NAŢIONAL DE MATEMATICA PANAITOPOL EDIŢIA a X-a, TULCEA, 21 aprilie 2018 Clasa a VII - a Soluţii orientative şi bareme Problema 1. Se conside
 CONCURSUL NAŢIONAL DE MATEMATICA PANAITOPOL EDIŢIA a X-a, TULCEA, 1 aprilie 18 Clasa a VII - a Soluţii orientative şi bareme Problema 1. Se consideră numerele reale x, y şi z, cel puţin două dintre ele
CONCURSUL NAŢIONAL DE MATEMATICA PANAITOPOL EDIŢIA a X-a, TULCEA, 1 aprilie 18 Clasa a VII - a Soluţii orientative şi bareme Problema 1. Se consideră numerele reale x, y şi z, cel puţin două dintre ele
