Slide 1
|
|
|
- Gabriel Tabacu
- 4 ani în urmă
- Vzualizari:
Transcriere
1 BAZELE ELECTOTEHNICII BE I An I - ETTI CUS 3 Conf. dr.ing.ec. Claudia PĂCUA Claudia.Pacurar@ethm.utcluj.ro
2 CICUITE ELECTICE DE CUENT CONTINUU
3 Teorema conservării puterilor Enunț: Puterea primită de un circuit pe la bornele sale de legătură cu exteriorul se consumă pe laturile circuitului. Se consideră un circuit care are legătură cu exteriorul prin bornele 1, 2,...,,..., m: Prin borna 1, potențialul și așa mai departe... V1 1 m l l V I = 1 = 1 j = 1 injecteză în circuit curentul = U I j j Dacă nu avem legătură cu exteriorul circuitul se numește izolat m = 1 VI = 0 primul termen este zero l l = 1 j= 1 U I j j = 0 I
4 Dacă aplicăm Legea lui Ohm pentru o latură de circuit avem: Uj Ej jij Ij + = și facem j l l l l l l 2 UjIj + EjIj = jij = 1 j = 1 = 1 j = 1 = 1 j = 1 ( ) = 0 în sistem izolat l l l l 2 EjIj = jij Bilanțul puterilor = 1 j = 1 = 1 j = 1 (conservarea puterilor) P G P P G = P
5 Enunț: Bilanțul puterilor (conservarea puterilor) puterea debitată de sursele dintr-un circuit se consumă pe rezistențele din acel circuit Observații: P G - puterea generată, este pozitivă în suma algebrică, dacă E și I au același sens, negativă în caz contrar (sumă algebrică); P - puterea consumată, este întotdeauna pozitivă (sumă aritmetică).
6 Teorema transferului maxim de putere (Transfer maxim de putere) Presupunem că avem o sursă de tensiune electromotoare reală, E, cu rezistența internă, i, care debitează (este conectată la) pe un rezistor (o sarcină), s Puterea transmisă rezistorului: P s = I s 2 Ce valoare trebuie să aibă rezistența să transmită putere maximă? s pentru ca sursa I = s 2 E E Ps = s + ( + ) i s i 2 Găsim maximul puterii prin anularea derivatei când Ps P 0 max = s
7 P s s 2 s + i 2 s 2 i s = E = E = E = s ( s + i ) ( s + i ) ( s + i ) ( s + i ) 0 i s = 0 i s = Condiția de transfer maxim de putere Condiția de transfer maxim de putere este îndeplinită atunci când rezistența de sarcină este egală cu rezistența internă a sursei. Puterea este maximă: 2 Pmax = si max E E I = P = + s 2 ( 2 ) max s 2 s i s = i P 2 2 E E = = 4 4 max s 2 s s s = i P max = E 2 = 4s s i
8 Observație: Dacă avem un circuit complex (cu o configurație mai complicată): Sursa debitează putere maximă când i =, unde AB AB este rezistența echivalentă a circuitului la bornele A și B
9 Metode de rezolvare a circuitelor electrice de curent continuu Metoda teoremelor lui Kirchhoff Presupune scrierea unui sistem de ecuații format din l ecuații, având l necunoscute, rezultat în urma aplicării Teoremei I a lui Kirchhoff pentru (n-s) noduri independente, respectiv aplicării Teoremei a II-a lui Kirchhoff pentru b bucle independente, calculate cu Teorema lui Euler, de forma: I = 0 N I = b, pentru (n-1) sau (n-s) noduri independente b E, pentru b= l -n+1 sau b= l -n+s bucle independente a) (n-1) sau (n-s) ecuații rezultate în urma aplicării Teoremei I a lui Kirchhoff pentru (n-1) sau (n-s) noduri independente, unde s reprezintă numărul reţelelor neconexe b) b= l -n+1 sau b= l -n+s ecuații rezultate în urma aplicării Teoremei a II-a lui Kirchhoff pentru b= l -n+1 sau b=l-n+s bucle independente
10 Fiind date: configurația rețelei electrice de curent continuu, valorile rezistențelor, și a surselor de tensiune, E, respective de curent, I g Se pot determina folosind metoda Teoremelor lui Kirchhoff: - curenții - tensiunile - puterile ETAPELE de aplicare ale metodei teoremelor lui irchhoff 1. Se analizează topologic circuitul pentru a stabili: - numărul de laturi, l ; - numărul de noduri, n; - numărul de rețele conexe, s; - numărul de bucle independente: b= l -n+1 sau b= l -n+s; - numărul de noduri independente: (n-1) sau (n-s). 2. Se stabilesc arbitrar sensuri de parcurgere pentru curenții din cele l laturi ale circuitului; 3. Se stabilesc arbitrar sensuri de parcurgere pentru cele b bucle independente;
11 4. Se scrie sistemul de ecuații corespunzător metodei teoremelor lui Kirchhoff de forma: I = 0 N I = b, pentru (n-1) sau (n-s) noduri independente b E, pentru b= l -n+1 sau b= l -n+s bucle independente 5. Se rezolvă sistemul de ecuații format din l ecuații și se determină cele l necunoscute (curenții din laturile circuitului) Observație: Curenții obținuți negativi în urma rezolvării sistemului au sens contrar celui arbitrar ales la etapa 2). Etape opționale: 6. Se calculează tensiunile; Modalități de verificare: 7. Se calculează puterile. 8. Se verifică rezolvarea corectă prin oricare din următoarele trei modalități posibile: a) Prin aplicarea Teoremei a II-a a lui Kirchhoff pe o altă buclă; b) Calculând tensiunea între două noduri pe minim două trasee diferite; c) Verificând conservarea puterilor (bilanțul puterilor).
12 ESTICȚII în aplicarea metodei teoremelor lui Kirchhoff (Surse ideale de curent) În cazul circuitelor care conțin surse ideale de curent există următoarele restricții în aplicarea metodei: a)latura care conține sursa ideală de curent,, poate fi cuprinsă într-o singură buclă independentă, deoarece prin sursa ideală de curent poate să treacă un singur sens de parcurgere, prin urmare cele b bucle independente se vor alege ținând cont de această observație; b)latura care conține sursa ideală de curent,, are conductanța nulă, rezistența infinită, prin urmare ecuația rezultată aplicând Teorema a II-a a lui Kirchhoff pentru bucla care conține sursa indelă de curent se va înlocui în sistemul specific metodei teoremelor lui Kirchhoff cu expresia: valoarea curentului din latura care conține sursa ideală de curent egală cu valoarea sursei ideale de curent, I g I g I g Un sistem de ecuații format din l ecuații, având (l - x) necunoscute, unde x reprezintă numărul surselor ideale din circuit
13 Metoda curenţilor ciclici (de ochiuri, de buclă, fictivi) În sistemul specific metodei teoremelor lui Kirchhoff are loc o substituție ingenioasă a necunoscutelor: în locul celor l curenți din laturi se introduc b= l - n+s curenți de buclă (ciclici sau de ochiuri). Se operează cu noi variabile numite curenți de ochiuri (de bucle sau ciclici). Curentul ciclic este un curent fictiv. Metoda presupune că, cele b= l - n+s bucle independente, sunt parcurse de curenți fictivi (de buclă) notați cu: ' ' ' I1, I2,..., I b Numărul ecuațiilor sistemului și numărul necunoscutelor se reduce de lal la b=l-n+s, deoarece primele (n-s) ecuații date de Teorema I a lui Kirchhoff dispar, devin identități. Curenții reali din laturile circuitului se vor determina ca sume algebrice ale tuturor curenților fictivi (ciclici), care concură (trec) prin latura respectivă.
14 Metoda presupune scrierea unui sistem de ecuații de forma: ' ' ' = 11I 1 12I2 1 bib E b1 I + I + + I = E ' ' ' b b b 2, b = l n + s I + I + + I = E b ' ' ' b1 1 b2 2 bb b b Este un sistem de ecuații compatibil, având b ecuații și b necunoscute. Curenții de buclă prin cele b bucle independente sunt notați cu: sensuri arbitrar alese și sunt necunoscutele sistemului. ' ' ' I1, I2,..., I b au
15 Termenii din sistem de forma: j b b = E reprezintă resistența proprie buclei independente și este egală cu suma aritmetică a tuturor rezistențelor din bucla independentă (întotdeauna pozitivă), j b 0 reprezintă rezistența comună buclelor independente și j (pozitivă ' ' dacă curenții fictivi I și au același sens prin latura comună și ' I negativă dacă și au sensuri opuse) j ' I j = sau < 0 j I j suma algebrică a tuturor tensiunilor electromotoare ale surselor care acționează în bucla independentă (se păstrează semnificația de la Teorema a II-a a lui Kirchhoff) sau < 0 b E (este pozitivă, dacă are același sens cu curentul fictiv E din bucla independentă, negativă în caz contrar) ' I
16 Se rezolvă sistemul de ecuații Curenții de buclă (fictivi) Curenții reali din laturile circuitului, ca fiind sume algebrice ale curenților fictivi (de buclă) care ar parcurge fictiv latura respectivă ESTICȚII în aplicarea metodei curenților ciclici (Surse ideale de curent) Sunt similare cu cele din cazul aplicării metodei teoremelor lui Kirchhoff pentru circuite electrice care conțin surse ideale de curent: a)latura care conține sursa ideală de curent va fi obligatoriu cuprinsă într-o singură buclă independentă, deoarece prin sursa ideală de curent poate să treacă un singur curent fictiv de buclă; b)ecuația corespunzătoare buclei independente care conține sursa ideală de curent se elimină și se înlocuiește în sistemul specific metodei curenților ciclici cu expresia: valoarea curentului fictiv de buclă egală cu valoarea sursei ideale de curent se reduce numărul necunoscutelor sistemului specific metodei, de la b necunoscute la (b-x) necunoscute, unde x reprezintă numărul surselor ideale din circuit
17 ETAPELE de aplicare ale metodei curenților ciclici: 1. Se analizează topologic circuitul: b, n, s,l 2. Se introduc curenți prin laturile circuitului cu sensuri arbitrar alese; 3. Se introduc curenții fictivi (de buclă) în cele b bucle independente cu sensuri arbitrar alese; 4. Se scrie sistemul de ecuații corespunzător metodei, format din b= l -n+s ecuații, având b necunoscute; 5. Se explicitează termenii din sistemul specific metodei; 6. Se rezolvă sistemul de ecuații și se determină curenții fictivi; 7. Se calculează curenții reali din laturile circuitului ca sume algebrice ale curenților fictivi care concură latura respectivă.
18 Metoda potențialelor nodurilor (tensiunilor nodale) - este o metodă duală; -în sistemul de ecuații corespunzător metodei teoremelor lui Kirchhoff se substituie necunoscutele astfel: în locul celor l curenți prin laturi se introduc (n-1) potențiale de noduri, după ce s-a ales arbitrar nodul neutilizat ca origine de potențial (potențial de referință), = 0 V n - se operează cu noi variabile numite potențialele nodurilor, egale ca număr cu numărul nodurilor independente (n-1) ale rețelei - se alege nodul n ca nod de referință, față de acest nod, celelalte noduri ale rețelei au potențialele: V 1, V 2... V, unde =n-1 - numărul ecuațiilor sistemului, ca și numărul necunoscutelor se reduce astfel de lal la (n-1), căci ultimele b ecuații ale sistemului specific metodei teoremelor lui Kirchhoff pentru buclele independente dispar, devenind identități
19 Metoda presupune scrierea unui sistem de ecuații de forma: G V + G V + + G V = I 1 G V + G V + + G V = I sc N n sc N 1 2, =n-1 G V + G V + + G V = I sc N - necunoscutele sistemului sunt cele (n-1) potențiale: V 1, V 2... V, unde =n-1
20 Termenii din sistem reprezintă: G Se numește conductanța proprie nodului și reprezintă suma conductanțelor laturilor care concură (se leagă) în nodul independent, ( G 0, întotdeauna pozitivă) G j = sc N I G j Se numește conductanța mutuală dintre nodurile independente și j și reprezintă suma cu semn schimbat a tuturor conductanțelor laturilor care leagă direct nodul de nodul j G. = G < 0 (întotdeauna negativă) j j - reprezintă curenții de scurtcircuit - intervin numai în laturile active (sunt injectați de către surse în nodul respectiv) - reprezintă suma algebrică a curenților de scurtcircuit injectați de surse în nodul respectiv,
21 Determinarea curenților de scurtcircuit injectați de: Sursa de tensiune: Sursa de curent: I sc E = = EG E = + sc N N I I g Suma este pozitivă dacă curenții de scurtcircuit sunt injectați în nod (sursele au sensul orientat (dirijat) înspre nodul considerat), negativă în caz contrar
22 Se rezolvă sistemul de ecuații și se obțin valorile necunoscutelor : V 1, V 2... V, unde =n-1 Curenţii reali din laturile circuitului se determină aplicând pe fiecare latură în parte Legea lui Ohm: U + E = I V1 V2 + E = I I V V + E = 1 2 I j = V V E (sau - E ) j j j j
23 ESTICȚII în aplicarea metodei potențialelor nodurilor (Surse ideale de tensiune) În cazul circuitelor care conțin surse ideale de tensiune metoda se poate aplica cu următoarele restricții: 1. Dacă în circuit există o sursă ideală de tensiune, atunci unul dintre nodurile laturii care conține această sursă se alege ca origine de potențial (potențial de referință), a.î. celălalt nod va avea potențialul egal cu valoarea sursei ideale de tensiune U = E 1 U = V 1 V 0 V V1 V0 = E = V = E 1 1 a.î. ecuația corespunzătoare metodei pentru acest nod se va înlocui cu: valoarea potențialului acestui nod egală cu valoarea sursei ideale de tensiune
24 2. Dacă în circuit există mai multe surse ideale de tensiune, apar dificultăți în aplicarea metodei, a.î. este necesară eliminarea unor surse ideale de tensiune cu ajutorul Teoremei lui Vaschy (lăsând în circuit doar o sursă ideală de tensiune) Observații: 1. Surse de curent Calculul curenților reali din laturile circuitului Dacă în circuit există surse de curent, rezistențele laturilor cu surse de curent se consideră, deci conductanța laturii va fi egală cu zero, a.î. curentul care parcurge latura care conține sursa de curent va avea exact valoarea sursei de curent, indiferent dacă în serie cu sursa de curent mai există alte surse de tensiune sau rezistențe 2. Surse ideale de tensiune Calculul curenților reali din laturile circuitului Curentul prin latura cu sursa ideală de tensiune se determină aplicând Teorema I a lui Kirchhoff pe nodul în care este legată latura cu sursa, după ce s-au determinat curenții prin celelalte laturi adiacente nodului respectiv
25 ETAPELE de aplicare a metodei potențialelor nodurilor 1. Se analizează topologic circuitul; 2. Se alege un nod drept nod de referință (origine de potențial), față de care necunoscutele sistemului specific metodei vor fi V 1, V 2... V n-1 3. Se scrie sistemul de ecuații corespunzător metodei potențialelor nodurilor, format din (n-1) ecuații și se explicitează termenii din sistem; 4. Se rezolvă sistemul și se determină valorile potențialelor; 5. Se determină curenții din laturile circuitului aplicând Legea lui Ohm pe fiecare latură în parte: V n = 0 I j V V E = j j j
26 Vă mulţumesc!!!
Slide 1
 Bazele electrotehnicii BAZELE ELECTOTEHNC BE An - ETT CS 4 Conf. dr.ing.ec. Claudia PĂCA e-mail: Claudia.Pacurar@ethm.utcluj.ro Bazele electrotehnicii CCTE ELECTCE DE CENT CONTN 7. Teoreme de rezolvare
Bazele electrotehnicii BAZELE ELECTOTEHNC BE An - ETT CS 4 Conf. dr.ing.ec. Claudia PĂCA e-mail: Claudia.Pacurar@ethm.utcluj.ro Bazele electrotehnicii CCTE ELECTCE DE CENT CONTN 7. Teoreme de rezolvare
Slide 1
 BAZELE ELECTOTEHNICII I BE An I - ETTI CS 2 Conf. dr.ing.ec. Claudia PĂCA e-mail: Claudia.Pacurar@ethm.utcluj.ro CAPITOLL I CICITE ELECTICE DE CENT CONTIN GENEALITĂȚI Circuitul electric de curent continuu
BAZELE ELECTOTEHNICII I BE An I - ETTI CS 2 Conf. dr.ing.ec. Claudia PĂCA e-mail: Claudia.Pacurar@ethm.utcluj.ro CAPITOLL I CICITE ELECTICE DE CENT CONTIN GENEALITĂȚI Circuitul electric de curent continuu
Slide 1
 ELECTROTEHNCĂ ET An - SA CRS 8 Conf.dr.ing.ec. Claudia PĂCRAR e-mail: Claudia.Pacurar@ethm.utcluj.ro . ntroducere în teoria circuitelor electrice. Puteri în regim armonic 3. Caracterizarea în complex a
ELECTROTEHNCĂ ET An - SA CRS 8 Conf.dr.ing.ec. Claudia PĂCRAR e-mail: Claudia.Pacurar@ethm.utcluj.ro . ntroducere în teoria circuitelor electrice. Puteri în regim armonic 3. Caracterizarea în complex a
Slide 1
 BAZELE ELECTROTEHNICII I BE An I - ETTI CURS 1 Conf. dr.ing.ec. Claudia PĂCURAR e-mail: Claudia.Pacurar@ethm.utcluj.ro BAZELE ELECTROTEHNICII I (BE) ETTI Curs Seria A - Prof. dr. ing. Vasile ȚOPA Vasile.Topa@ethm.utcluj.ro
BAZELE ELECTROTEHNICII I BE An I - ETTI CURS 1 Conf. dr.ing.ec. Claudia PĂCURAR e-mail: Claudia.Pacurar@ethm.utcluj.ro BAZELE ELECTROTEHNICII I (BE) ETTI Curs Seria A - Prof. dr. ing. Vasile ȚOPA Vasile.Topa@ethm.utcluj.ro
Electricitate II
 Electricitate II Circuitul electric. Legile circuitului electric. Sumar Circuitul electric simplu Legile lui Ohm Legile lui Kirchhoff Gruparea rezistorilor Transformarea stea-triunghi Gruparea generatoarelor
Electricitate II Circuitul electric. Legile circuitului electric. Sumar Circuitul electric simplu Legile lui Ohm Legile lui Kirchhoff Gruparea rezistorilor Transformarea stea-triunghi Gruparea generatoarelor
Direct Current (DC) Electric Circuits
 ELECTROTEHNICA BIBLIOGRAFIE 1. VINȚAN MARIA - Note de curs 2. POPA MIRCEA, VINŢAN MARIA, Electrotehnică. Îndrumar de laborator, Editura Universităţii Lucian Blaga din Sibiu, ISBN 9736512053, 2001, cota
ELECTROTEHNICA BIBLIOGRAFIE 1. VINȚAN MARIA - Note de curs 2. POPA MIRCEA, VINŢAN MARIA, Electrotehnică. Îndrumar de laborator, Editura Universităţii Lucian Blaga din Sibiu, ISBN 9736512053, 2001, cota
I
 METODA VECTORIALĂ ÎN GEOMETRIE prof. Andrei - Octavian Dobre Această metodă poate fi descrisă după cum urmează: Fiind dată o problemă de geometrie, după explicitarea şi reprezentarea grafică a configuraţiei
METODA VECTORIALĂ ÎN GEOMETRIE prof. Andrei - Octavian Dobre Această metodă poate fi descrisă după cum urmează: Fiind dată o problemă de geometrie, după explicitarea şi reprezentarea grafică a configuraţiei
Cursul 12 (plan de curs) Integrale prime 1 Sisteme diferenţiale autonome. Spaţiul fazelor. Fie Ω R n o mulţime deschisă şi f : Ω R n R n o funcţie de
 Cursul 12 (plan de curs) Integrale prime 1 Sisteme diferenţiale autonome. Spaţiul fazelor. Fie Ω R n o mulţime deschisă şi f : Ω R n R n o funcţie de clasă C 1. Vom considera sistemul diferenţial x = f(x),
Cursul 12 (plan de curs) Integrale prime 1 Sisteme diferenţiale autonome. Spaţiul fazelor. Fie Ω R n o mulţime deschisă şi f : Ω R n R n o funcţie de clasă C 1. Vom considera sistemul diferenţial x = f(x),
Microsoft Word - cap1p4.doc
 Algebră liniară, geometrie analitică şi diferenţială.6 Subspaţii vectoriale Fie V un spaţiu vectorial peste corpul K. În cele ce urmează vom introduce două definiţii echivalente pentru noţiunea de subspaţiu
Algebră liniară, geometrie analitică şi diferenţială.6 Subspaţii vectoriale Fie V un spaţiu vectorial peste corpul K. În cele ce urmează vom introduce două definiţii echivalente pentru noţiunea de subspaţiu
FILTRE DE REALIZARE CU CIRCUITE DE INTEGRARE
 FILTRE ACTIVE BIQUAD REALIZATE CU CIRCUITE DE INTEGRARE. SCOPUL LUCRĂRII Măsurători asupra unor filtre active biquad de tip RC realizate cu circuite de integrare.. ASPECTE TEORETICE Considerăm funcţia
FILTRE ACTIVE BIQUAD REALIZATE CU CIRCUITE DE INTEGRARE. SCOPUL LUCRĂRII Măsurători asupra unor filtre active biquad de tip RC realizate cu circuite de integrare.. ASPECTE TEORETICE Considerăm funcţia
1
 4.3. Amplificatoare de semnal mic Amplificatoarele de semnal mic (ASM) au semnalul amplificat mic în raport cu tensiunile de c.c. de polarizare a tranzistoarelor. Tranzistoarele funcţionează într-o zonă
4.3. Amplificatoare de semnal mic Amplificatoarele de semnal mic (ASM) au semnalul amplificat mic în raport cu tensiunile de c.c. de polarizare a tranzistoarelor. Tranzistoarele funcţionează într-o zonă
Cursul 7 Formula integrală a lui Cauchy Am demonstrat în cursul precedent că, dacă D C un domeniu simplu conex şi f : D C o funcţie olomorfă cu f cont
 Cursul 7 Formula integrală a lui Cauchy Am demonstrat în cursul precedent că, dacă D C un domeniu simplu conex şi f : D C o funcţie olomorfă cu f continuă pe D, atunci, pe orice curbă rectificabilă şi
Cursul 7 Formula integrală a lui Cauchy Am demonstrat în cursul precedent că, dacă D C un domeniu simplu conex şi f : D C o funcţie olomorfă cu f continuă pe D, atunci, pe orice curbă rectificabilă şi
Teoreme cu nume 1. Problema (Năstăsescu IX, p 147, propoziţia 5) Formula lui Chasles Pentru orice puncte M, N şi P avem MN + NP = MP.
 Teoreme cu nume Problema (Năstăsescu IX, p 47, propoziţia 5) Formula lui hasles Pentru orice puncte M, N şi P avem MN + NP = MP 2 Problema (Năstăsescu IX, p 68, teoremă) Vectorul de poziţie al centrului
Teoreme cu nume Problema (Năstăsescu IX, p 47, propoziţia 5) Formula lui hasles Pentru orice puncte M, N şi P avem MN + NP = MP 2 Problema (Năstăsescu IX, p 68, teoremă) Vectorul de poziţie al centrului
Microsoft PowerPoint - Curs_SDA_9_RO_2019_v2.pptx
 SDA (PC2) Curs 9 Liste / Grafuri / Arbori Iulian Năstac Lista dublu înlănțuită Recapitulare Într-o astfel de listă fiecare nod conţine doi pointeri: unul spre nodul următor şi unul spre nodul precedent.
SDA (PC2) Curs 9 Liste / Grafuri / Arbori Iulian Năstac Lista dublu înlănțuită Recapitulare Într-o astfel de listă fiecare nod conţine doi pointeri: unul spre nodul următor şi unul spre nodul precedent.
PowerPoint Presentation
 Electronică Analogică Redresoare Redresoare polifazate, comandate redresoarele comandate permit reglarea tensiunii şi a curentului prin sarcină. Reglajul poate fi făcut în mod continuu de la zero până
Electronică Analogică Redresoare Redresoare polifazate, comandate redresoarele comandate permit reglarea tensiunii şi a curentului prin sarcină. Reglajul poate fi făcut în mod continuu de la zero până
Facultatea de Matematică Anul II Master, Geometrie Algebrică Mulţimi algebrice ireductibile. Dimensiune 1 Mulţimi ireductibile Propoziţia 1.1. Fie X u
 Facultatea de Matematică Anul II Master, Geometrie Algebrică Mulţimi algebrice ireductibile. Dimensiune 1 Mulţimi ireductibile Propoziţia 1.1. Fie X un spaţiu topologic. Următoarele afirma-ţii sunt echivalente:
Facultatea de Matematică Anul II Master, Geometrie Algebrică Mulţimi algebrice ireductibile. Dimensiune 1 Mulţimi ireductibile Propoziţia 1.1. Fie X un spaţiu topologic. Următoarele afirma-ţii sunt echivalente:
2.1.Tipul tablou unidimensional
 7. Grafuri 7.1. Grafuri neorientate - Teste grilă 1. V_88_I_5. Care este numărul minim de noduri pe care îl poate conţine un graf neorientat cu 50 de muchii, şi în care 15 noduri sunt izolate? a. 25 b.
7. Grafuri 7.1. Grafuri neorientate - Teste grilă 1. V_88_I_5. Care este numărul minim de noduri pe care îl poate conţine un graf neorientat cu 50 de muchii, şi în care 15 noduri sunt izolate? a. 25 b.
Microsoft Word - probleme_analiza_numerica_ses_ian09.rtf
 Universitatea Spiru Haret Facultatea de Matematica-Informatica Disciplina obligatorie; Anul 3, Sem. 1,Matematica si Informatica CONTINUTUL TEMATIC AL DISCIPLINEI Metode numerice de rezolvare a sistemelor
Universitatea Spiru Haret Facultatea de Matematica-Informatica Disciplina obligatorie; Anul 3, Sem. 1,Matematica si Informatica CONTINUTUL TEMATIC AL DISCIPLINEI Metode numerice de rezolvare a sistemelor
Calcul Numeric
 Calcul Numeric Cursul 4 2019 Anca Ignat Metode numerice de rezolvarea sistemelor liniare Fie matricea nesingulară A nn şi b n. Rezolvarea sistemului de ecuații liniare Ax=b se poate face folosind regula
Calcul Numeric Cursul 4 2019 Anca Ignat Metode numerice de rezolvarea sistemelor liniare Fie matricea nesingulară A nn şi b n. Rezolvarea sistemului de ecuații liniare Ax=b se poate face folosind regula
Gheorghe IUREA Adrian ZANOSCHI algebră geometrie clasa a VII-a ediţia a V-a, revizuită mate 2000 standard EDITURA PARALELA 45 Matematică. Clasa a VII-
 Gheorghe IUREA Adrian ZANOSCHI algebră geometrie clasa a VII-a ediţia a V-a, revizuită mate 2000 standard 3 Algebră Capitolul I. MULŢIMEA NUMERELOR RAŢIONALE Identificarea caracteristicilor numerelor raţionale
Gheorghe IUREA Adrian ZANOSCHI algebră geometrie clasa a VII-a ediţia a V-a, revizuită mate 2000 standard 3 Algebră Capitolul I. MULŢIMEA NUMERELOR RAŢIONALE Identificarea caracteristicilor numerelor raţionale
Grafuri - Concepte de baza. Tipuri de grafuri. Modalitati de reprezentare
 Concepte de bază. Tipuri de grafuri. Modalităţi de reprezentare Mircea Marin Departamentul of Informatică Universitatea de Vest din Timişoara mircea.marin@e-uvt.ro 9 noiembrie 2018 Introducere Ce este
Concepte de bază. Tipuri de grafuri. Modalităţi de reprezentare Mircea Marin Departamentul of Informatică Universitatea de Vest din Timişoara mircea.marin@e-uvt.ro 9 noiembrie 2018 Introducere Ce este
ETTI-AM2, , M. Joița & A. Niță Notițe de Adrian Manea Seminar 11 Transformarea Laplace Aplicații Transformarea Z Ecuații și sisteme diferenți
 Seminar Transformarea Laplace Aplicații Transformarea Z Ecuații și sisteme diferențiale Folosind transformata Laplace, putem reolva ecuații și sisteme diferențiale. Cu ajutorul proprietăților transformatei
Seminar Transformarea Laplace Aplicații Transformarea Z Ecuații și sisteme diferențiale Folosind transformata Laplace, putem reolva ecuații și sisteme diferențiale. Cu ajutorul proprietăților transformatei
Subiecte
 Cap. Semnale şi instrumente pentru generarea lor. Ce tipuri de aparate pot genera semnal sinusoidal? 2. Care sunt principalele caracteristici ale unui generator de audio frecvenţă? 3. Care sunt principalele
Cap. Semnale şi instrumente pentru generarea lor. Ce tipuri de aparate pot genera semnal sinusoidal? 2. Care sunt principalele caracteristici ale unui generator de audio frecvenţă? 3. Care sunt principalele
Matematica VI
 There are no translations available. Datorita unor probleme tehnice, site-ul nu poate fi vizionat cu Internet Explorer 8, partea de teste (apare pagina alba). Pentru navigare, va recomandam Chrome, Mozilla,
There are no translations available. Datorita unor probleme tehnice, site-ul nu poate fi vizionat cu Internet Explorer 8, partea de teste (apare pagina alba). Pentru navigare, va recomandam Chrome, Mozilla,
Retele Petri si Aplicatii
 Reţele Petri şi Aplicaţii Curs 3 RPA (2019) Curs 3 1 / 48 Conţinutul cursului 1 Arbori de acoperire 2 Probleme de decizie în reţele Petri 3 Invarianţi tranziţie RPA (2019) Curs 3 2 / 48 Arbori de acoperire
Reţele Petri şi Aplicaţii Curs 3 RPA (2019) Curs 3 1 / 48 Conţinutul cursului 1 Arbori de acoperire 2 Probleme de decizie în reţele Petri 3 Invarianţi tranziţie RPA (2019) Curs 3 2 / 48 Arbori de acoperire
Slide 1
 ELECTROTEHNICĂ ET An I - ISA CURS 13 Conf.dr.ing.ec. Claudia PĂCURAR e-mail: Claudia.Pacurar@ehm.ucluj.ro REGIMUL TRANZITORIU AL CIRCUITELOR ELECTRICE LINIARE Generaliăţi Definiţie Regimul elecrocineic
ELECTROTEHNICĂ ET An I - ISA CURS 13 Conf.dr.ing.ec. Claudia PĂCURAR e-mail: Claudia.Pacurar@ehm.ucluj.ro REGIMUL TRANZITORIU AL CIRCUITELOR ELECTRICE LINIARE Generaliăţi Definiţie Regimul elecrocineic
Prelegerea 4 În această prelegere vom învăţa despre: Algebre booleene; Funcţii booleene; Mintermi şi cuburi n - dimensionale. 4.1 Definirea algebrelor
 Prelegerea 4 În această prelegere vom învăţa despre: Algebre booleene; Funcţii booleene; Mintermi şi cuburi n - dimensionale. 4.1 Definirea algebrelor booleene Definiţia 4.1 Se numeşte algebră Boole (booleană)
Prelegerea 4 În această prelegere vom învăţa despre: Algebre booleene; Funcţii booleene; Mintermi şi cuburi n - dimensionale. 4.1 Definirea algebrelor booleene Definiţia 4.1 Se numeşte algebră Boole (booleană)
Microsoft Word - TIC5
 CAPACITATEA CANALELOR DE COMUNICAŢIE CAPITOLUL 5 CAPACITATEA CANALELOR DE COMUNICAŢIE În Capitolul 3, am văzut că putem utiliza codarea sursă pentru a reduce redundanţa inerentă a unei surse de informaţie
CAPACITATEA CANALELOR DE COMUNICAŢIE CAPITOLUL 5 CAPACITATEA CANALELOR DE COMUNICAŢIE În Capitolul 3, am văzut că putem utiliza codarea sursă pentru a reduce redundanţa inerentă a unei surse de informaţie
PROGRAMA ANALITICĂ PENTRU CLASA A X-A, CURSURI DE EXCELENŢĂ ANUL ŞCOLAR Studiul fizicii în clasele de excelenţă are ca finalitate încheierea
 PROGRAMA ANALITICĂ PENTRU CLASA A X-A, CURSURI DE EXCELENŢĂ ANUL ŞCOLAR 2015-2016 Studiul fizicii în clasele de excelenţă are ca finalitate încheierea dezvoltării la elevi a unui set specific de competenţe-cheie
PROGRAMA ANALITICĂ PENTRU CLASA A X-A, CURSURI DE EXCELENŢĂ ANUL ŞCOLAR 2015-2016 Studiul fizicii în clasele de excelenţă are ca finalitate încheierea dezvoltării la elevi a unui set specific de competenţe-cheie
METODE NUMERICE ÎN INGINERIE
 METODE NUMERICE ÎN INGINERIE REZOLVAREA NUMERICĂ A SISTEMELOR DE ECUATII LINIARE Aspecte generale (1) (2) (3) (4) (5) Unicitatea soluţiei Un sistem de ecuaţii liniare are o soluţie unică numai dacă matricea
METODE NUMERICE ÎN INGINERIE REZOLVAREA NUMERICĂ A SISTEMELOR DE ECUATII LINIARE Aspecte generale (1) (2) (3) (4) (5) Unicitatea soluţiei Un sistem de ecuaţii liniare are o soluţie unică numai dacă matricea
CURBE BÉZIER În CAGD se utilizează adesea curbele polinomiale, adică acele curbe definite de o parametrizare polinomială: C : [a, b] R 3 C(t) = (x(t),
![CURBE BÉZIER În CAGD se utilizează adesea curbele polinomiale, adică acele curbe definite de o parametrizare polinomială: C : [a, b] R 3 C(t) = (x(t), CURBE BÉZIER În CAGD se utilizează adesea curbele polinomiale, adică acele curbe definite de o parametrizare polinomială: C : [a, b] R 3 C(t) = (x(t),](/thumbs/101/150500936.jpg) CURE ÉZIER În CAGD se utilizează adesea curbele polinomiale, adică acele curbe definite de o parametrizare polinomială: C : [a, b] R 3 C(t) = (x(t), y(t), z(t)) cu x, y, z polinoame de grad n. Maximul
CURE ÉZIER În CAGD se utilizează adesea curbele polinomiale, adică acele curbe definite de o parametrizare polinomială: C : [a, b] R 3 C(t) = (x(t), y(t), z(t)) cu x, y, z polinoame de grad n. Maximul
Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică Gheorghe Asachi Iaşi, 2015 Analiză Matematică Lucian Maticiuc 1 / 29
 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică Gheorghe Asachi Iaşi, 2015 Analiză Matematică Lucian Maticiuc 1 / 29 Definiţie. Şiruri mărginite. Şiruri monotone. Subşiruri ale
Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică Gheorghe Asachi Iaşi, 2015 Analiză Matematică Lucian Maticiuc 1 / 29 Definiţie. Şiruri mărginite. Şiruri monotone. Subşiruri ale
Microsoft Word - C05_Traductoare de deplasare de tip transformator
 Traductoare de deplasare de tip transformator Traductoare parametrice. Principiul de funcţionare: Modificarea inductivităţii mutuale a unor bobine cu întrefier variabil sau constant. Ecuaţia care exprimă
Traductoare de deplasare de tip transformator Traductoare parametrice. Principiul de funcţionare: Modificarea inductivităţii mutuale a unor bobine cu întrefier variabil sau constant. Ecuaţia care exprimă
Elemente de aritmetica
 Elemente de aritmetică Anul II Februarie 2017 Divizibilitate în Z Definiţie Fie a, b Z. Spunem că a divide b (scriem a b) dacă există c Z astfel încât b = ac. In acest caz spunem că a este un divizor al
Elemente de aritmetică Anul II Februarie 2017 Divizibilitate în Z Definiţie Fie a, b Z. Spunem că a divide b (scriem a b) dacă există c Z astfel încât b = ac. In acest caz spunem că a este un divizor al
PowerPoint Presentation
 ELEMENTE DE MORFOLOGIE MATEMATICA Morfologia matematica Cadru de abordare diferit: Pana acum : Imaginea este o functie de doua variabile. Pixelii imaginii (valori si coordonate de pozitie) sunt structurati
ELEMENTE DE MORFOLOGIE MATEMATICA Morfologia matematica Cadru de abordare diferit: Pana acum : Imaginea este o functie de doua variabile. Pixelii imaginii (valori si coordonate de pozitie) sunt structurati
Slide 1
 Proiectarea optimală a dispozitivelor electromagnetice PROIECTAREA OPTIMALĂ A DISPOZITIVELOR ELECTROMAGNETICE PODE CURS 2 Conf.dr.ing.ec. Claudia PĂCURAR e-mail: Claudia.Pacurar@et.utcluj.ro 2/46 Proiectarea
Proiectarea optimală a dispozitivelor electromagnetice PROIECTAREA OPTIMALĂ A DISPOZITIVELOR ELECTROMAGNETICE PODE CURS 2 Conf.dr.ing.ec. Claudia PĂCURAR e-mail: Claudia.Pacurar@et.utcluj.ro 2/46 Proiectarea
Microsoft Word - DCE - lucrarea 5.doc
 LUCRAREA 5 TRANZISTORUL CU EFECT DE CÂMP CU POARTĂ JONCŢIUNE 5.1. Prezentare teoretică Tranzistorul cu efect de câmp cu poartă joncţiune este un dispozitiv electronic cu patru electrozi (D-dreană, S-sursă,
LUCRAREA 5 TRANZISTORUL CU EFECT DE CÂMP CU POARTĂ JONCŢIUNE 5.1. Prezentare teoretică Tranzistorul cu efect de câmp cu poartă joncţiune este un dispozitiv electronic cu patru electrozi (D-dreană, S-sursă,
carteInvataturaEd_2.0_lectia5.pdf
 Lect ia3 Diagrame Veitch-Karnaugh 5.1 Noţiuni teoretice Diagramele Veich-Karnaugh (V-K) sunt o modalitate de reprezentare grafică a funcţiilor logice. Pentru o funct ie de N variabile, diagrama corespunz
Lect ia3 Diagrame Veitch-Karnaugh 5.1 Noţiuni teoretice Diagramele Veich-Karnaugh (V-K) sunt o modalitate de reprezentare grafică a funcţiilor logice. Pentru o funct ie de N variabile, diagrama corespunz
Slide 1
 ELECTROTEHNICĂ ET A I - IA CUR 6 Cof.dr.ig.ec. Claudia PĂCURAR e-mail: Claudia.Pacurar@ethm.utcluj.ro . Legea iducției electromagetice 2. Eergii și forțe î câmp magetic . Legea iducției electromagetice
ELECTROTEHNICĂ ET A I - IA CUR 6 Cof.dr.ig.ec. Claudia PĂCURAR e-mail: Claudia.Pacurar@ethm.utcluj.ro . Legea iducției electromagetice 2. Eergii și forțe î câmp magetic . Legea iducției electromagetice
Cursul 8 Funcţii analitice Vom studia acum comportarea şirurilor şi seriilor de funcţii olomorfe, cu scopul de a dezvălui o proprietate esenţială a ac
 Cursul 8 Funcţii analitice Vom studia acum comportarea şirurilor şi seriilor de funcţii olomorfe, cu scopul de a dezvălui o proprietate esenţială a acestor funcţii: analiticitatea. Ştim deja că, spre deosebire
Cursul 8 Funcţii analitice Vom studia acum comportarea şirurilor şi seriilor de funcţii olomorfe, cu scopul de a dezvălui o proprietate esenţială a acestor funcţii: analiticitatea. Ştim deja că, spre deosebire
D.Rusu, Teoria măsurii şi integrala Lebesgue 6 MĂSURA LEBESGUE Cursul 5 Teorema 6.26 Există submulţimi ale lui R care nu sunt măsurabile Lebesgue. Dem
 D.Rusu, Teoria măsurii şi integrala Lebesgue 6 MĂSURA LEBESGUE Cursul 5 Teorema 6.26 Există submulţimi ale lui R care nu sunt măsurabile Lebesgue. Demonstraţie. Fie mulţimea A = [0, ], pe care definim
D.Rusu, Teoria măsurii şi integrala Lebesgue 6 MĂSURA LEBESGUE Cursul 5 Teorema 6.26 Există submulţimi ale lui R care nu sunt măsurabile Lebesgue. Demonstraţie. Fie mulţimea A = [0, ], pe care definim
FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituţia de învăţământ superior Universitatea Alexandru Ioan Cuza din Iaşi 1.2 Facultatea Facultatea de
 FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituţia de învăţământ superior Universitatea Alexandru Ioan Cuza din Iaşi 1.2 Facultatea Facultatea de Matematică 1.3 Departamentul Matematică Didactic 1.4
FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituţia de învăţământ superior Universitatea Alexandru Ioan Cuza din Iaşi 1.2 Facultatea Facultatea de Matematică 1.3 Departamentul Matematică Didactic 1.4
Microsoft Word - IngineriF_A.DOC
 Se considera v BE 0.6V in conductie si β00. Pentru v I.6+0.05sinωt [V], tensiunea este : +0V R C 5K v I v BE 0.5mA 0V C a 7.50.3sinωt [V] c.5.5sinωt [V] b 7.5.5sinωt [V] d.60.05sinωt [V] Se cunoaste β00
Se considera v BE 0.6V in conductie si β00. Pentru v I.6+0.05sinωt [V], tensiunea este : +0V R C 5K v I v BE 0.5mA 0V C a 7.50.3sinωt [V] c.5.5sinωt [V] b 7.5.5sinωt [V] d.60.05sinωt [V] Se cunoaste β00
Consultatii ELa123, 06 ianuarie 2014
 Consultatii ELa123, 06 ianuarie 2014 Paul Ulmeanu January 6, 2014 Paul Ulmeanu () Consultatii ELa123, 06 ianuarie 2014 January 6, 2014 1 / 22 Cuprins 1 Cuprins 2 Principii 3 Logica sistemului Date de intrare
Consultatii ELa123, 06 ianuarie 2014 Paul Ulmeanu January 6, 2014 Paul Ulmeanu () Consultatii ELa123, 06 ianuarie 2014 January 6, 2014 1 / 22 Cuprins 1 Cuprins 2 Principii 3 Logica sistemului Date de intrare
gaussx.dvi
 Algebră liniarăi 1 Recapitulare cunoştiinţe de algebră din clasa XI-a În clasa a XI s-a studiat la algebră problema existenţei soluţiei 1 şi calculării soluţiei sistemelor liniare 2 (adică sisteme care
Algebră liniarăi 1 Recapitulare cunoştiinţe de algebră din clasa XI-a În clasa a XI s-a studiat la algebră problema existenţei soluţiei 1 şi calculării soluţiei sistemelor liniare 2 (adică sisteme care
GHEORGHE PROCOPIUC PROBLEME DE ANALIZĂ MATEMATICĂ ŞI ECUAŢII DIFERENŢIALE IAŞI, 2007
 GHEORGHE PROCOPIUC PROBLEME DE ANALIZĂ MATEMATICĂ ŞI ECUAŢII DIFERENŢIALE IAŞI, 7 Cuprins Elemente de teoria spaţiilor metrice 4 Spaţii metrice 4 Mulţimea numerelor reale 8 Şiruri şi serii 5 Şiruri de
GHEORGHE PROCOPIUC PROBLEME DE ANALIZĂ MATEMATICĂ ŞI ECUAŢII DIFERENŢIALE IAŞI, 7 Cuprins Elemente de teoria spaţiilor metrice 4 Spaţii metrice 4 Mulţimea numerelor reale 8 Şiruri şi serii 5 Şiruri de
Tiberiu Trif Analiză matematică 2 Calcul diferențial și integral în R n
 Tiberiu Trif Analiză matematică 2 Calcul diferențial și integral în R n Cuprins Notații v 1 Topologie în R n 1 1.1 Spațiul euclidian R n........................ 1 1.2 Structura topologică a spațiului
Tiberiu Trif Analiză matematică 2 Calcul diferențial și integral în R n Cuprins Notații v 1 Topologie în R n 1 1.1 Spațiul euclidian R n........................ 1 1.2 Structura topologică a spațiului
Aero-BCD, , Prof. L. Costache & M. Olteanu Notițe de Adrian Manea Seminar 5 Șiruri și serii de funcții. Serii de puteri 1 Șiruri de funcții D
 Seminar 5 Șiruri și serii de funcții. Serii de puteri Șiruri de funcții Definiţie.: Fie (f n ) n un șir de funcții, cu fiecare f n : [a, b] R și fie o funcție f : [a, b] R. PC Spunem că șirul (f n ) converge
Seminar 5 Șiruri și serii de funcții. Serii de puteri Șiruri de funcții Definiţie.: Fie (f n ) n un șir de funcții, cu fiecare f n : [a, b] R și fie o funcție f : [a, b] R. PC Spunem că șirul (f n ) converge
Capitolul MD. 10 Metoda funcţiilor Liapunov Fie sistemul diferenţial x = f (t, x), t t 0, x D R n. (10.1) Presupunem că x = 0 este punct de echilibru,
 Capitolul MD. 10 Metoda funcţiilor Liapunov Fie sistemul diferenţial x = f (t, x), t t 0, x D R n. (10.1) Presupunem că x = 0 este punct de echilibru, adică f (t, 0) = 0, t t 0. In acest paragraf, funcţia
Capitolul MD. 10 Metoda funcţiilor Liapunov Fie sistemul diferenţial x = f (t, x), t t 0, x D R n. (10.1) Presupunem că x = 0 este punct de echilibru, adică f (t, 0) = 0, t t 0. In acest paragraf, funcţia
Ministerul Educaţiei, Cercetării şi Tineretului Subiecte pentru Faza naţională a Olimpiadelor la disciplinele din aria curriculară Tehnologii 30 APRIL
 Subiecte pentru Faza naţională a Olimpiadelor la disciplinele din aria curriculară Tehnologii 30 APRILIE 2008 Profil: tehnic Calificarea: tehnician electrotehnist Clasa: XII Ruta progresivă OLIMPIADA DISCIPLINE
Subiecte pentru Faza naţională a Olimpiadelor la disciplinele din aria curriculară Tehnologii 30 APRILIE 2008 Profil: tehnic Calificarea: tehnician electrotehnist Clasa: XII Ruta progresivă OLIMPIADA DISCIPLINE
ExamView Pro - Untitled.tst
 Class: Date: Subiecte logica computationala licenta matematica-informatica 4 ani Multiple Choice Identify the letter of the choice that best completes the statement or answers the question. 1. Fie formula
Class: Date: Subiecte logica computationala licenta matematica-informatica 4 ani Multiple Choice Identify the letter of the choice that best completes the statement or answers the question. 1. Fie formula
Microsoft Word - L25Ro_Studiul efectului Hall_f_RF
 STUDIUL EFECTULUI ALL 1. Scopul lucrării Obiectivul acestei lucrări este: punerea în evidenţă a efectului all pentru un semiconductor intrinsec, măsurarea tensiunii all, determinarea constantei all, a
STUDIUL EFECTULUI ALL 1. Scopul lucrării Obiectivul acestei lucrări este: punerea în evidenţă a efectului all pentru un semiconductor intrinsec, măsurarea tensiunii all, determinarea constantei all, a
2
 C4: Structuri nanocristaline. Modelul Kronig-Penney 1. Stucturi cuantice traditionale Reducerea dimensionalităţii unui sistem fizic (de exemplu material semiconductor) produsă prin confinarea particulelor
C4: Structuri nanocristaline. Modelul Kronig-Penney 1. Stucturi cuantice traditionale Reducerea dimensionalităţii unui sistem fizic (de exemplu material semiconductor) produsă prin confinarea particulelor
Subiectul 1
 Subiectul 1 În fişierul Numere.txt pe prima linie este memorat un număr natural n (n
Subiectul 1 În fişierul Numere.txt pe prima linie este memorat un număr natural n (n
Grafuri neorinetate Aplicatii 1 Care este numărul maxim de componente conexe pe care le poate avea un graf neorientat cu 20 noduri şi 12 muchii? a. 6
 Grafuri neorinetate Aplicatii 1 Care este numărul maxim de componente conexe pe care le poate avea un graf neorientat cu 20 noduri şi 12 muchii? a. 6 b. 12 c. 10 d. 15 2 Câte grafuri neorientate, distincte,
Grafuri neorinetate Aplicatii 1 Care este numărul maxim de componente conexe pe care le poate avea un graf neorientat cu 20 noduri şi 12 muchii? a. 6 b. 12 c. 10 d. 15 2 Câte grafuri neorientate, distincte,
Dorel LUCHIAN Gabriel POPA Adrian ZANOSCHI Gheorghe IUREA algebră geometrie clasa a VIII-a ediţia a V-a, revizuită mate 2000 standard EDITURA PARALELA
 Dorel LUCHIAN Gabriel POPA Adrian ZANOSCHI Gheorghe IUREA algebră geometrie clasa a VIII-a ediţia a V-a, revizuită mate 000 standard 3 10 PP Algebră Capitolul I. NUMERE REALE Competenţe specifice: Determinarea
Dorel LUCHIAN Gabriel POPA Adrian ZANOSCHI Gheorghe IUREA algebră geometrie clasa a VIII-a ediţia a V-a, revizuită mate 000 standard 3 10 PP Algebră Capitolul I. NUMERE REALE Competenţe specifice: Determinarea
Lucian L. TURDEANU Georgeta D. POP (MANEA) BAZELE GEOMETRICE ALE FOTOGRAMETRIEI CONSPRESS BUCUREŞTI 2009
 Lucian L. TURDEANU Georgeta D. POP (MANEA) BAZELE GEOMETRICE ALE FOTOGRAMETRIEI CONSPRESS BUCUREŞTI 2009 CUPRINS Pg. INTRODUCERE. Noţiuni preliminare (L. Turdeanu, G. Pop)... 6 Probleme... 11 1. GEOMETRIA
Lucian L. TURDEANU Georgeta D. POP (MANEA) BAZELE GEOMETRICE ALE FOTOGRAMETRIEI CONSPRESS BUCUREŞTI 2009 CUPRINS Pg. INTRODUCERE. Noţiuni preliminare (L. Turdeanu, G. Pop)... 6 Probleme... 11 1. GEOMETRIA
Slide 1
 SCTR -SZOKE ENIKO - Curs 4 continuare curs 3 3. Componentele hard ale unui sistem de calcul in timp real 3.1 Unitatea centrala de calcul 3.1.1 Moduri de adresare 3.1.2 Clase de arhitecturi ale unitatii
SCTR -SZOKE ENIKO - Curs 4 continuare curs 3 3. Componentele hard ale unui sistem de calcul in timp real 3.1 Unitatea centrala de calcul 3.1.1 Moduri de adresare 3.1.2 Clase de arhitecturi ale unitatii
Paradigme de Programare
 Paradigme de Programare Conf. dr. ing. Andrei Olaru andrei.olaru@cs.pub.ro cs@andreiolaru.ro Departamentul de Calculatoare 2019 9 : 1 / 38 Cursul 9 Concluzie Paradigma Funcțională 9 : 2 / 38 Cursul 9:
Paradigme de Programare Conf. dr. ing. Andrei Olaru andrei.olaru@cs.pub.ro cs@andreiolaru.ro Departamentul de Calculatoare 2019 9 : 1 / 38 Cursul 9 Concluzie Paradigma Funcțională 9 : 2 / 38 Cursul 9:
Noțiuni matematice de bază
 Sistem cartezian definitie. Coordonate carteziene Sistem cartezian definiţie Un sistem cartezian de coordonate (coordonatele carteziene) reprezintă un sistem de coordonate plane ce permit determinarea
Sistem cartezian definitie. Coordonate carteziene Sistem cartezian definiţie Un sistem cartezian de coordonate (coordonatele carteziene) reprezintă un sistem de coordonate plane ce permit determinarea
Logică și structuri discrete Logică propozițională Marius Minea marius/curs/lsd/ 3 noiembrie 2014
 Logică și structuri discrete Logică propozițională Marius Minea marius@cs.upt.ro http://www.cs.upt.ro/ marius/curs/lsd/ 3 noiembrie 2014 Unde aplicăm verificarea realizabilității? probleme de căutare și
Logică și structuri discrete Logică propozițională Marius Minea marius@cs.upt.ro http://www.cs.upt.ro/ marius/curs/lsd/ 3 noiembrie 2014 Unde aplicăm verificarea realizabilității? probleme de căutare și
E_d_Informatica_sp_SN_2014_bar_10_LRO
 Examenul de bacalaureat naţional 2014 Proba E. d) Informatică Varianta 10 Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu. Timpul de lucru efectiv este de 3 ore. În rezolvările cerute,
Examenul de bacalaureat naţional 2014 Proba E. d) Informatică Varianta 10 Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu. Timpul de lucru efectiv este de 3 ore. În rezolvările cerute,
COMENTARII FAZA JUDEŢEANĂ, 9 MARTIE 2013 Abstract. Personal comments on some of the problems presented at the District Round of the National Mathemati
 COMENTARII FAZA JUDEŢEANĂ, 9 MARTIE 2013 Abstract. Personal comments on some of the problems presented at the District Round of the National Mathematics Olympiad 2013. Data: 12 martie 2013. Autor: Dan
COMENTARII FAZA JUDEŢEANĂ, 9 MARTIE 2013 Abstract. Personal comments on some of the problems presented at the District Round of the National Mathematics Olympiad 2013. Data: 12 martie 2013. Autor: Dan
U.T.Cluj-Napoca, C.U.N. Baia Mare Facultatea: Inginerie PLAN de INVĂŢĂMÂNT Domeniul: Inginerie Energetică anul univ Program licenţă: Ingine
 Domeniul: Inginerie Energetică anul univ. 2015-2016 Anul I Cod 1 Analiză matematică I 2 2 N 1 28 28 74 5 DF 2 Algebră liniară, geometrie analitică şi diferentială 2 2 N 1 28 28 74 5 DF 3 Fizică 2 1 1 N
Domeniul: Inginerie Energetică anul univ. 2015-2016 Anul I Cod 1 Analiză matematică I 2 2 N 1 28 28 74 5 DF 2 Algebră liniară, geometrie analitică şi diferentială 2 2 N 1 28 28 74 5 DF 3 Fizică 2 1 1 N
UNIVERSITATEA DE VEST DIN TIMIȘOARA FACULTATEA DE FIZICA CONCURSUL NAȚIONAL DE FIZICĂ CONSTANTIN SĂLCEANU 30 MARTIE 2019 Sunt obligatorii toate subiec
 UNIVERSITATEA DE VEST DIN TIMIȘOARA FACULTATEA DE FIZICA CONCURSUL NAȚIONAL DE FIZICĂ CONSTANTIN SĂLCEANU 30 MARTIE 2019 Sunt obligatorii toate subiectele din două arii tematice (la alegere) dintre cele
UNIVERSITATEA DE VEST DIN TIMIȘOARA FACULTATEA DE FIZICA CONCURSUL NAȚIONAL DE FIZICĂ CONSTANTIN SĂLCEANU 30 MARTIE 2019 Sunt obligatorii toate subiectele din două arii tematice (la alegere) dintre cele
Notiuni de algebra booleana
 Noţiuni de algebră booleană (în lucru) Definiţie Algebră booleană = o structură algebrică formată din: O mulţime B Două operaţii binare notate cu (+) şi (.) O operaţie unară notată cu ( ) pentru care sunt
Noţiuni de algebră booleană (în lucru) Definiţie Algebră booleană = o structură algebrică formată din: O mulţime B Două operaţii binare notate cu (+) şi (.) O operaţie unară notată cu ( ) pentru care sunt
Fâciu N. Maria-Ema CASA CORPULUI DIDACTIC BRĂILA PROGRAM DE FORMARE INFORMATICĂ ȘI TIC PENTRU GIMNAZIU CLASA A V-A SERIA 1 GRUPA 2 CURSANT: Fâciu N. M
 CASA CORPULUI DIDACTIC BRĂILA PROGRAM DE FORMARE INFORMATICĂ ȘI TIC PENTRU GIMNAZIU CLASA A V-A SERIA 1 GRUPA 2 CURSANT: PROIECTUL UNITĂŢII DE ÎNVĂŢARE ALGORITMI Notă: filmele didactice, dezbaterile, jocurile
CASA CORPULUI DIDACTIC BRĂILA PROGRAM DE FORMARE INFORMATICĂ ȘI TIC PENTRU GIMNAZIU CLASA A V-A SERIA 1 GRUPA 2 CURSANT: PROIECTUL UNITĂŢII DE ÎNVĂŢARE ALGORITMI Notă: filmele didactice, dezbaterile, jocurile
Microsoft Word - TST05.00.docx
 FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituția de învățământ superior Universitatea Tehnică din Cluj-Napoca 1.2 Facultatea Facultatea de Electronică, Telecomunicații și Tehnologia Informației 1.3
FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituția de învățământ superior Universitatea Tehnică din Cluj-Napoca 1.2 Facultatea Facultatea de Electronică, Telecomunicații și Tehnologia Informației 1.3
Microsoft Word - Matematika_kozep_irasbeli_javitasi_0911_roman.doc
 Matematika román nyelven középszint 0911 ÉRETTSÉGI VIZSGA 011. május. MATEMATIKA ROMÁN NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ NEMZETI ERŐFORRÁS MINISZTÉRIUM Indicaţii
Matematika román nyelven középszint 0911 ÉRETTSÉGI VIZSGA 011. május. MATEMATIKA ROMÁN NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ NEMZETI ERŐFORRÁS MINISZTÉRIUM Indicaţii
Spatii vectoriale
 Algebra si Geometrie Seminar 2 Octombrie 2017 ii Matematica poate fi definită ca materia în care nu ştim niciodată despre ce vorbim, nici dacă ceea ce spunem este adevărat. Bertrand Russell 1 Spatii vectoriale
Algebra si Geometrie Seminar 2 Octombrie 2017 ii Matematica poate fi definită ca materia în care nu ştim niciodată despre ce vorbim, nici dacă ceea ce spunem este adevărat. Bertrand Russell 1 Spatii vectoriale
Slide 1
 BAELE ELECTOTEHNC BE An - ETT CUS 9 Conf. dr.ng.ec. Clauda PĂCUA e-mal: Clauda.Pacurar@et.utcluj.ro CCUTE ELECTCE LNAE ÎN EGM PEMANENT SNUSODAL TEOEME Ș METODE DE ANALĂ A CCUTELO ELECTCE LNAE 3/36 Conf.dr.ng.ec.
BAELE ELECTOTEHNC BE An - ETT CUS 9 Conf. dr.ng.ec. Clauda PĂCUA e-mal: Clauda.Pacurar@et.utcluj.ro CCUTE ELECTCE LNAE ÎN EGM PEMANENT SNUSODAL TEOEME Ș METODE DE ANALĂ A CCUTELO ELECTCE LNAE 3/36 Conf.dr.ng.ec.
LOGICA MATEMATICA SI COMPUTATIONALA Sem. I,
 LOGICA MATEMATICĂ ŞI COMPUTAŢIONALĂ Sem. I, 2017-2018 Ioana Leustean FMI, UB Partea III Calculul propoziţional clasic Consistenţă şi satisfiabilitate Teorema de completitudine Algebra Lindenbaum-Tarski
LOGICA MATEMATICĂ ŞI COMPUTAŢIONALĂ Sem. I, 2017-2018 Ioana Leustean FMI, UB Partea III Calculul propoziţional clasic Consistenţă şi satisfiabilitate Teorema de completitudine Algebra Lindenbaum-Tarski
Prelegerea 3 În această prelegere vom învăţa despre: Clase speciale de latici: complementate. modulare, metrice, distributive şi 3.1 Semi-distributivi
 Prelegerea 3 În această prelegere vom învăţa despre: Clase speciale de latici: complementate. modulare, metrice, distributive şi 3.1 Semi-distributivitate şi semi - modularitate Fie L o latice. Se numeşte
Prelegerea 3 În această prelegere vom învăţa despre: Clase speciale de latici: complementate. modulare, metrice, distributive şi 3.1 Semi-distributivitate şi semi - modularitate Fie L o latice. Se numeşte
2
 C5: Metoda matricilor de transfer BIBLIOGRAFIE E. Tulcan Paulescu, M. Paulescu Algorithms for electronic states in artificial semiconductors of use in intermediate band solar cells engineering. In Physics
C5: Metoda matricilor de transfer BIBLIOGRAFIE E. Tulcan Paulescu, M. Paulescu Algorithms for electronic states in artificial semiconductors of use in intermediate band solar cells engineering. In Physics
Fisa disciplinei_Utilizarea_Calc_CFDP_ _var2_
 UNIVERSITATEA TEHNICĂ DE CONSTRUCȚII BUCUREȘTI FIŞA DISCIPLINEI (COD PO-09_F-01) Denumirea Utilizarea calculatoarelor Codul 1.OB05.DPF Anul de studiu I Semestrul 1 Tipul de evaluare finală (E, CO, V) CO
UNIVERSITATEA TEHNICĂ DE CONSTRUCȚII BUCUREȘTI FIŞA DISCIPLINEI (COD PO-09_F-01) Denumirea Utilizarea calculatoarelor Codul 1.OB05.DPF Anul de studiu I Semestrul 1 Tipul de evaluare finală (E, CO, V) CO
Microsoft Word - Prezcap1.doc
 CAPITOLUL 1: NOŢIUNI DE METROLOGIE 1.1 TERMINOLOGIE Măsurarea; Măsură şi măsurare; Metrologia; Metoda de măsură; Principiul de măsură; Procesul de măsură; Rezultatul măsurării; Exactitatea măsurării; Incertitudinea
CAPITOLUL 1: NOŢIUNI DE METROLOGIE 1.1 TERMINOLOGIE Măsurarea; Măsură şi măsurare; Metrologia; Metoda de măsură; Principiul de măsură; Procesul de măsură; Rezultatul măsurării; Exactitatea măsurării; Incertitudinea
TEORIA MĂSURII Liviu C. Florescu Universitatea Al.I.Cuza, Facultatea de Matematică, Bd. Carol I, 11, R Iaşi, ROMANIA, e mail:
 TEORI MĂSURII Liviu C. Florescu Universitatea l.i.cuza, Facultatea de Matematică, Bd. Carol I, 11, R 700506 Iaşi, ROMNI, e mail: lflo@uaic.ro În mod intenţionat această pagină este lăsată albă! Cuprins
TEORI MĂSURII Liviu C. Florescu Universitatea l.i.cuza, Facultatea de Matematică, Bd. Carol I, 11, R 700506 Iaşi, ROMNI, e mail: lflo@uaic.ro În mod intenţionat această pagină este lăsată albă! Cuprins
L4. TEOREMELE ALGEBREI BINARE. FUNCȚII LOGICE ELEMENTARE. OPERAȚII LOGICE PE BIT. SINTEZA FUNCȚIILOR LOGICE DIN TABELE DE ADEVĂR 1. Obiective Prin par
 L4. TEOREMELE LGEBREI BINRE. FUNCȚII LOGICE ELEMENTRE. OPERȚII LOGICE PE BIT. SINTEZ FUNCȚIILOR LOGICE DIN TBELE DE DEVĂR 1. Obiective Prin parcurgerea acestei ședințe de laborator studenții vor fi capabili:
L4. TEOREMELE LGEBREI BINRE. FUNCȚII LOGICE ELEMENTRE. OPERȚII LOGICE PE BIT. SINTEZ FUNCȚIILOR LOGICE DIN TBELE DE DEVĂR 1. Obiective Prin parcurgerea acestei ședințe de laborator studenții vor fi capabili:
Cuprins
 Cuprins 1. Introducere 2. Modele și limbaje pentru specificația sistemelor 3. Interfețe de comunicație 4. Periferice pentru sisteme dedicate 5. Microcontrolere 6. Procesoare dedicate 7. Dezvoltarea programelor
Cuprins 1. Introducere 2. Modele și limbaje pentru specificația sistemelor 3. Interfețe de comunicație 4. Periferice pentru sisteme dedicate 5. Microcontrolere 6. Procesoare dedicate 7. Dezvoltarea programelor
FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituţia de învăţământ superior Universitatea Alexandru Ioan Cuza din Iaşi 1.2 Facultatea Facultatea de
 FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituţia de învăţământ superior Universitatea Alexandru Ioan Cuza din Iaşi 1.2 Facultatea Facultatea de Matematică 1.3 Departamentul Matematică Didactic 1.4
FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituţia de învăţământ superior Universitatea Alexandru Ioan Cuza din Iaşi 1.2 Facultatea Facultatea de Matematică 1.3 Departamentul Matematică Didactic 1.4
Microsoft Word - ST96m Rezistor.doc
 Societatea Comercială ELECTRICA SA Bucureşti SPECIFICAŢIE TEHNICĂ Rezistor de limitare a curentului de defect pentru tratarea neutrului reţelelor de MT S.T. nr. 96 Rev. 0 1 2 Data 2010 Nr. pagini: 5 CUPRINS
Societatea Comercială ELECTRICA SA Bucureşti SPECIFICAŢIE TEHNICĂ Rezistor de limitare a curentului de defect pentru tratarea neutrului reţelelor de MT S.T. nr. 96 Rev. 0 1 2 Data 2010 Nr. pagini: 5 CUPRINS
REGULAMENT
 UNIVERSITATEA VASILE ALECSANDRI din BACĂU Facultatea de Inginerie Calea Mărăşeşti, Nr. 157, Bacău, 600115, Tel./Fax +40 234 580170 http://inginerie.ub.ro; e-mail: decaning@ub.ro FIŞA DISCIPLINEI (licenţă)
UNIVERSITATEA VASILE ALECSANDRI din BACĂU Facultatea de Inginerie Calea Mărăşeşti, Nr. 157, Bacău, 600115, Tel./Fax +40 234 580170 http://inginerie.ub.ro; e-mail: decaning@ub.ro FIŞA DISCIPLINEI (licenţă)
Microsoft Word - Planuri_Mate_
 ANUL I 2018-2019 (TRUNCHI COMUN pentru programele de studii universitare de licență: MATEMATICĂ, MATEMATICĂ- INFORMATICĂ, MATEMATICI APLICATE) I 1. Algebră 3 3 E 6 3 3 E 7 2. Analiză matematică 3 3 E 6
ANUL I 2018-2019 (TRUNCHI COMUN pentru programele de studii universitare de licență: MATEMATICĂ, MATEMATICĂ- INFORMATICĂ, MATEMATICI APLICATE) I 1. Algebră 3 3 E 6 3 3 E 7 2. Analiză matematică 3 3 E 6
Laborator 4 Modele sistemice liniare. Reprezentare numerică. Conversii. Conexiuni 4.1 Tema Formarea deprinderilor de utilizare a convenţiilor MATLAB d
 Laborator 4 Modele sistemice liniare Reprezentare numerică Conversii Conexiuni 41 Tema Formarea deprinderilor de utilizare a convenţiilor MATLAB de reprezentare numerică a modelelor sitemice de stare şi
Laborator 4 Modele sistemice liniare Reprezentare numerică Conversii Conexiuni 41 Tema Formarea deprinderilor de utilizare a convenţiilor MATLAB de reprezentare numerică a modelelor sitemice de stare şi
COMISIA EUROPEANĂ Bruxelles, COM(2018) 274 final ANNEX 1 ANEXĂ la Propunerea de DIRECTIVĂ A PARLAMENTULUI EUROPEAN ȘI A CONSILIULUI de modif
 COMISIA EUROPEANĂ Bruxelles, 17.5.2018 COM(2018) 274 final ANNEX 1 ANEXĂ la Propunerea de DIRECTIVĂ A PARLAMENTULUI EUROPEAN ȘI A CONSILIULUI de modificare a Directivei 2008/96/CE privind gestionarea siguranței
COMISIA EUROPEANĂ Bruxelles, 17.5.2018 COM(2018) 274 final ANNEX 1 ANEXĂ la Propunerea de DIRECTIVĂ A PARLAMENTULUI EUROPEAN ȘI A CONSILIULUI de modificare a Directivei 2008/96/CE privind gestionarea siguranței
MULTIMETRU DIGITAL AX-585 INSTRUCŢIUNI DE UTILIZARE
 MULTIMETRU DIGITAL AX-585 INSTRUCŢIUNI DE UTILIZARE 1. Informaţii generale. 3 2. Informaţii privind siguranţa. 3 3. Funcţii 3 4. Operarea aparatului de măsură. 6 5. Întreţinerea aparatului. 9 6. Rezolvarea
MULTIMETRU DIGITAL AX-585 INSTRUCŢIUNI DE UTILIZARE 1. Informaţii generale. 3 2. Informaţii privind siguranţa. 3 3. Funcţii 3 4. Operarea aparatului de măsură. 6 5. Întreţinerea aparatului. 9 6. Rezolvarea
MD.09. Teoria stabilităţii 1
 MD.09. Teoria stabilităţii 1 Capitolul MD.09. Teoria stabilităţii Cuvinte cheie Soluţie stabilă spre +, instabilă si asimptotic stabilă, punct de echilibru, soluţie staţionară, stabilitatea soluţiei banale,
MD.09. Teoria stabilităţii 1 Capitolul MD.09. Teoria stabilităţii Cuvinte cheie Soluţie stabilă spre +, instabilă si asimptotic stabilă, punct de echilibru, soluţie staţionară, stabilitatea soluţiei banale,
DAN LASCU ADRIANA-LIGIA SPORIŞ ANDA OLTEANU PAUL VASILIU MATEMATICĂ. CULEGERE DE PROBLEME TIP GRILĂ PENTRU ADMITEREA ÎN ACADEMIA NAVALĂ MIRCEA CEL BĂT
 DAN LASCU ADRIANA-LIGIA SPORIŞ ANDA OLTEANU PAUL VASILIU MATEMATICĂ. CULEGERE DE PROBLEME TIP GRILĂ PENTRU ADMITEREA ÎN ACADEMIA NAVALĂ MIRCEA CEL BĂTRÂN Colecţia Matematică DAN LASCU ADRIANA-LIGIA SPORIŞ
DAN LASCU ADRIANA-LIGIA SPORIŞ ANDA OLTEANU PAUL VASILIU MATEMATICĂ. CULEGERE DE PROBLEME TIP GRILĂ PENTRU ADMITEREA ÎN ACADEMIA NAVALĂ MIRCEA CEL BĂTRÂN Colecţia Matematică DAN LASCU ADRIANA-LIGIA SPORIŞ
Laboratorul numărul 12 Transformatorul pentru sudură Pentru a realiza aprinderea și întreținerea în cele mai bune condiții este necesar ca transformat
 Laboratorul numărul 12 Transformatorul pentru sudură Pentru a realiza aprinderea și întreținerea în cele mai bune condiții este necesar ca transformatoarele de sudură să aibă tensiunea de funcţionare în
Laboratorul numărul 12 Transformatorul pentru sudură Pentru a realiza aprinderea și întreținerea în cele mai bune condiții este necesar ca transformatoarele de sudură să aibă tensiunea de funcţionare în
Microsoft Word - 12 Emilia PAUSAN.doc
 CONFERINȚA NAȚIONALĂ DE INSTRUMENTAȚIE VIRTUALĂ, EDIȚIA A V-A, BUCURE TI, MAI 2008 53 Experimente simple cu achiziție de semnal Profesor Emilia Păuşan, Liceul Teoretic Tudor Vladimirescu, Bucureşti Abstract
CONFERINȚA NAȚIONALĂ DE INSTRUMENTAȚIE VIRTUALĂ, EDIȚIA A V-A, BUCURE TI, MAI 2008 53 Experimente simple cu achiziție de semnal Profesor Emilia Păuşan, Liceul Teoretic Tudor Vladimirescu, Bucureşti Abstract
CURRICULUM VITAE
 8.4. Calculul stabilizatorului 1 Schema stabilizatorului 1 este prezentată în figura 8.7. Fig. 8.7. Schema stabilizatorului 1, cu diodă zener şi tranzistor Date de pornire pentru stabilizatorul 1: U 1
8.4. Calculul stabilizatorului 1 Schema stabilizatorului 1 este prezentată în figura 8.7. Fig. 8.7. Schema stabilizatorului 1, cu diodă zener şi tranzistor Date de pornire pentru stabilizatorul 1: U 1
Lecții de pregă,re la informa,că Admitere 2019 Tema: Discutarea problemelor date la ul,mele sesiuni de admitere Bogdan Alexe
 Lecții de pregă,re la informa,că Admitere 2019 Tema: Discutarea problemelor date la ul,mele sesiuni de admitere Bogdan Alexe bogdan.alexe@fmi.unibuc.ro Cuprinsul lecției de azi Enunțuri și rezolvări pentru
Lecții de pregă,re la informa,că Admitere 2019 Tema: Discutarea problemelor date la ul,mele sesiuni de admitere Bogdan Alexe bogdan.alexe@fmi.unibuc.ro Cuprinsul lecției de azi Enunțuri și rezolvări pentru
{ 3x + 3, x < 1 Exemple. 1) Fie f : R R, f(x) = 2x + 4, x 1. Funcţia f este derivabilă pe R\{1} (compunere de funcţii elementare), deci rămâne să stud
 { 3 + 3, < Eemple. ) Fie f : R R, f() + 4,. Funcţia f este derivabilă pe R\{} (compunere de funcţii elementare), deci rămâne să studiem derivabilitatea în a. Atunci f s() 3+3 6,< 3, f d f() f() (),> funcţia
{ 3 + 3, < Eemple. ) Fie f : R R, f() + 4,. Funcţia f este derivabilă pe R\{} (compunere de funcţii elementare), deci rămâne să studiem derivabilitatea în a. Atunci f s() 3+3 6,< 3, f d f() f() (),> funcţia
Fizica fluidelor Cursul 5
 Fizica fluidelor Cursul 5 Victor E. Ambruș Universitatea de Vest din Timișoara Capitolul III. Curgeri potențiale. III.1. Fluidul perfect. III.2. Teorema lui Bernoulli. III.3. Echilibrul hidrostatic. III.4.
Fizica fluidelor Cursul 5 Victor E. Ambruș Universitatea de Vest din Timișoara Capitolul III. Curgeri potențiale. III.1. Fluidul perfect. III.2. Teorema lui Bernoulli. III.3. Echilibrul hidrostatic. III.4.
Logică și structuri discrete Limbaje regulate și automate Marius Minea marius/curs/lsd/ 24 noiembrie 2014
 Logică și structuri discrete Limbaje regulate și automate Marius Minea marius@cs.upt.ro http://www.cs.upt.ro/ marius/curs/lsd/ 24 noiembrie 2014 Un exemplu: automatul de cafea acțiuni (utilizator): introdu
Logică și structuri discrete Limbaje regulate și automate Marius Minea marius@cs.upt.ro http://www.cs.upt.ro/ marius/curs/lsd/ 24 noiembrie 2014 Un exemplu: automatul de cafea acțiuni (utilizator): introdu
Investeşte în oameni
 FIŞA DISCIPLINEI 1 1. Date despre program 1.1 Instituţia de învăţământ superior Universitatea Politehnică Timișoara 1. Facultatea / Departamentul 3 Facultatea de Inginerie Hunedoara / Inginerie Electrică
FIŞA DISCIPLINEI 1 1. Date despre program 1.1 Instituţia de învăţământ superior Universitatea Politehnică Timișoara 1. Facultatea / Departamentul 3 Facultatea de Inginerie Hunedoara / Inginerie Electrică
Microsoft PowerPoint - ARI_R_c9-10_IP_part2 [Compatibility Mode]
![Microsoft PowerPoint - ARI_R_c9-10_IP_part2 [Compatibility Mode] Microsoft PowerPoint - ARI_R_c9-10_IP_part2 [Compatibility Mode]](/thumbs/99/143164776.jpg) 2.1.2.2.2 Divizarea în subreţele de dimensiuni variabile Divizarea în subreţele de dimensiuni variabile sau cu măşti de subreţea de lungime diferită, VLSM (variable length subnet masks) subreţelele obţinute
2.1.2.2.2 Divizarea în subreţele de dimensiuni variabile Divizarea în subreţele de dimensiuni variabile sau cu măşti de subreţea de lungime diferită, VLSM (variable length subnet masks) subreţelele obţinute
Instrucţiuni pentru montarea şi utilizarea hotei AG 2
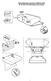 Instrucţiuni pentru montarea şi utilizarea hotei SL 16.1/SL 16 P IX/HA (Hotă de bucătărie) 1 Filtru anti-grăsimi Filtru cu suport metalic Filtru pe cărbuni 2 Bec halogen Bec de 40 W Instrucţiuni de montare
Instrucţiuni pentru montarea şi utilizarea hotei SL 16.1/SL 16 P IX/HA (Hotă de bucătărie) 1 Filtru anti-grăsimi Filtru cu suport metalic Filtru pe cărbuni 2 Bec halogen Bec de 40 W Instrucţiuni de montare
MULTIMETRU DIGITAL CU SCHIMBARE AUTOMATĂ A DOMENIULUI AX201 INSTRUCŢIUNI DE UTILIZARE
 MULTIMETRU DIGITAL CU SCHIMBARE AUTOMATĂ A DOMENIULUI AX201 INSTRUCŢIUNI DE UTILIZARE CITIŢI CU ATENŢIE INSTRUCŢIUNILE ÎNAINTE DE ÎNCEPEREA LUCRULUI GARANŢIA Producătorul garantează că aparatul nu va prezenta
MULTIMETRU DIGITAL CU SCHIMBARE AUTOMATĂ A DOMENIULUI AX201 INSTRUCŢIUNI DE UTILIZARE CITIŢI CU ATENŢIE INSTRUCŢIUNILE ÎNAINTE DE ÎNCEPEREA LUCRULUI GARANŢIA Producătorul garantează că aparatul nu va prezenta
