Geometrie afină Conf. Univ. Dr. Cornel Pintea cpintea math.ubbcluj.ro Cuprins 1 Săptămâna 1 Structura afină a unui spaţiu vectorial Vari
|
|
|
- Stanca Marin
- 4 ani în urmă
- Vzualizari:
Transcriere
1 Geometrie afină Conf Univ Dr Cornel Pintea cpintea mathubbclujro Cuprins 1 Săptămâna 1 Structura afină a unui spaţiu vectorial 1 11 Varietăţi liniare 1 12 Spaţiul director şi dimensiunea unei varietăţi liniare 1 13 Intersecţia unei familii de varietăţi liniare 2 Apendix Relaţii de recurenţă liniare 2 14 Probleme 6 2 Săptămâna Învelitori şi combinaţii afine Dreptele unui spaţiu afin Probleme 14 3 Săptămâna Teorema dimensiunii Paralelism Probleme 18 4 Săptămâna 4: Proprietăţi laticeale Mulţimi convexe Proprietăţi laticeale ale structurii afine Structura afină a spaţiului vectorial K n Submulţimile convexe ale unui spaţiu vectorial real Teorema lui Carathéodory Probleme 24 5 Săptămâna 5 Teoremele lui Radon, Helly, Minkowsky, Krein-Milman şi Motzkin Teorema lui Radon Teorema lui Helly Teoremele lui Minkowski, Krein-Milman şi Motzkin Probleme 28 6 Săptămâna 6: Spaţiul afin Definiţie şi exemple Subspaţii afine Combinaţii afine în spaţii afine Repere afine şi repere carteziene 33 1
2 65 Schimbarea coordonatelor Probleme 35 7 Săptămâna Funcţii polinomiale Definiţii şi observaţii Funcţii polinomiale de gradul doi Reprezentări matriceale 41 8 Săptămâna 8: Reducerea izometrică a polinoamelor de gradul doi în două variabile Invarianţi ortogonali Semiinvarianţi ortogonali Probleme 45 9 Săptămâna 9: Teorema de reducere izometrică a polinoamelor de gradul doi în două variabile Probleme Săptămâna 10: Reducerea izometrică a polinoamelor de gradul doi în trei variabile Invarianţi şi semiinvarianţi ortogonali Invarianţi ortogonali Semiinvarianţi ortogonali Teorema de reducere izometrică a polinoamelor de gradul doi în trei variabile Probleme Săptămâna 11 Morfisme liniare şi aplicaţii afine Ecuaţiile unei aplicaţii afine Imaginile inverse ale unei aplicaţii afine Teorema dimensiunii Funcţionale afine Hiperplane Translaţia Subspaţii invariante Omotetii Probleme Săptămâna 12 Proiecţii şi simetrii Proiecţii Ecuaţiile proiecţiilor Simetrii Ecuaţiile simetriilor Translaţiile ca produse de simetrii Probleme Apendix Proiecţii şi simetrii vectoriale Proiecţii vectoriale Simetrii vectoriale Săptămâna 13 Izometriile spaţiului afin euclidian Definiţii şi rezultate preliminare Teorema Cartan-Dieudonné Săptămâna 14 Perpendicularitate şi distanţe Distanţa de la un punct la un hiperplan Distanţa de la un punct la o varietate liniară 88 2
3 Coordonator: Conf Univ Dr Cornel Pintea Departmentul de Mathematică, Universitatea Babeş-Bolyai M Kogălniceanu 1, Cluj-Napoca, România 3
4 1 Săptămâna 1 Structura afină a unui spaţiu vectorial 11 Varietăţi liniare Fie V un spaţiu vectorial cu scalari într-un corp K Definiţia 11 O varietate liniară în V este o submulţime a lui V de forma a + U := {a + u u U}, unde a V şi U este un subspaţiu vectorial al lui V, sau mulţimea vidă Mulţimea A(V) a varietăţilor liniare ale lui V ordonată de incluziune se numeşte structura afină a lui V Propoziţia 11 Dacă A = a + U A(V) şi b A, atunci A = b + U Corolarul 12 O varietate liniară A este subspaţiu vectorial dacă şi numai dacă 0 A 12 Spaţiul director şi dimensiunea unei varietăţi liniare Propoziţia 13 Dacă a + U = a + U A(V), atunci U = U Aşadar, în reprezentarea unei varietăţi liniare nevide A sub forma a + U, subspaţiul vectorial U este unic determinat de A Acesta va fi notat cu D(A) şi se va numi (sub)spaţiul (vectorial) director al varietăţii liniare A Definiţia 12 Spunem că varietăţile liniare A, B A(V) sunt paralele, şi scriem A B, dacă D(A) D(B) sau D(B) D(A) Definiţia 13 Definim dimensiunea unei varietăţi liniare A astfel: { dim(d(a)) dacă A = dim(a) := 1 dacă A = Definiţia 14 Dacă dim(a) = 1, 2 sau p, atunci A se numeşte dreaptă, plan sau p-plan Dacă dim(a) = 0, atunci A este formată dintr-un singur element numit punct Dacă 0 A, atunci A se numeşte dreaptă vectorială, plan vectorial sau p-plan vectorial Dacă D(A) este un hiperplan vectorial, atunci A = a + D(A) se numeşte hiperplan Dacă V este un spaţiu vectorial n-dimensional, atunci orice hiperplan al lui V are dimensiunea n 1 Propoziţia 14 Fie V, W două spaţii vectoriale peste corpul K şi f : V W o aplicaţie liniară Dacă B este o varietate liniară a lui W, adică B A(W), atunci f 1 (B) := {a V f (a) B} este o varietate liniară a lui V, adică f 1 (B) A(V) Cornel Pintea Page 1 of 89 Babeş-Bolyai University 2016
5 Corolarul 15 Fie V şi W două spaţii vectoriale peste corpul K şi f : V W o aplicaţie liniară Dacă B A(W) este astfel încât f 1 (B) = şi a f 1 (B), atunci f 1 (B) = a + f 1 (D(B)), fapt care arată că D ( f 1 (B) ) = f 1 (D(B)) În particular, dacă pentru un element b W avem f 1 (b) = şi a f 1 (b), atunci D ( f 1 (b) ) = f 1 (0 W ) = ker( f ), adică f 1 (b) = a + ker( f ) Aşadar soluţia generală a ecuaţiei neomogene f (x) = b este suma dintre o soluţie particulară a ecuaţiei neomogene f (x) = b cu soluţia generală a ecuaţiei omogene f (x) = 0 W 13 Intersecţia unei familii de varietăţi liniare Propoziţia 16 Dacă {A i } i I este o familie de varietăţi liniare ale spaţiului vectorial V, atunci A i A(V) i I Corolarul 17 Dacă ( {A i } i I ) este o familie de varietăţi liniare ( ale spaţiului ) vectorial ( V astfel ) încât A i =, atunci D A i = D(A i ) În acest caz dim A i = dim D(A i ) i I i I i I Propoziţia 18 Dacă a şi b sunt puncte distincte în V, atunci există o singură dreaptă, notată cu ab, care conţine pe a şi b i I i I Apendix Relaţii de recurenţă liniare Fie K este un corp Notăm prin K N mulţime tuturor şirurilor de elemente din K, adică mulţime tuturor funcţiilor a : N K Vom nota cu a(n) sau cu a n valoarea funcţiei a pe Cornel Pintea Page 2 of 89 Babeş-Bolyai University 2016
6 numărul natural n În cazul al doilea, vom nota cu (a n ) n 0 sau, simplu, cu (a n ) şirul/funcţia a Dacă α K şi a, b K N, definim şirurile a + b, a b şi α a prin (a + b)(n) := a(n) + b(n) (a b)(n) := a(n)b(n) şi (α a)(n) = αa(n), sau, echivalent, (a + b) n = a n + b n şi (α a) n = αa n, for all n N Mulţimea K N este evident un K-spaţiu vectorial faţă de operaţiile: Putem scrie aceste operaţii astfel: K N K N K N, (a, b) a + b (11) K K N K N, (α, a) α a (12) K N K N K N, ((a n ), (b n )) (a n ) + (b n ) := (a n + b n ) (13) K K N K N, (α, (a n )) α (a n ) := (αa n ) (14) De fapt K N este chiar o K-algebră faţă de operaţiile (11), (12) şi K N K N K N, (a, b) a b sau (15) K N K N K N, ((a n ), (b n )) (a n ) (b n ) := (a n b n ) (16) De altfel operaţia externă (12) (sau (14)) poate fi obţinută din operaţia binară (15) (sau (16)) prin restricţia scalarilor de la K N la K K N Într-adevăr K se scufundă în K N prin incluziunea care asociază scalarului k K şirul constant (k n ), adică k n = k pentru orice n N Observăm că spaţiul vectorial K N este infinit dimensional deoarece submulţimea sa infinită {e 1, e 2, e 3,, }, unde e 1 := (1, 0, 0, ), e 2 := (0, 1, 0, ), e 3 := (0, 0, 1, ), este liberă (liniar independentă) De asemenea orice funcţie R : K N K N de tipul R(a n ) n 0 = (c r (n)a n+r + c r 1 (n)a n+r c 0 (n)a n ) n 0, unde c 0,, c r K N sunt r şiruri date, este liniară Aşadar imaginea inversă { } R 1 ( f ) := a K N : c r (n)a n+r + c r 1 (n)a n+r c 0 (n)a n = f (n), n 0 a unui şir f K N este o varietate liniară a lui K N a cărui direcţie este subspţiul { } ker R = R 1 (0) = a K N : c r (n)a n+r + c r 1 (n)a n+r c 0 (n)a n = 0, n 0 Ecuaţia c r (n)a n+r + c r 1 (n)a n+r c 0 (n)a n = f (n), n 0, (17) care defineşte varietatea liniară R 1 ( f ), se numeşte relaţie de recurenţă liniară neomogenă de ordin r, iar ecuaţia c r (n)a n+r + c r 1 (n)a n+r c 0 (n)a n = 0, n 0, (18) care defineşte subspaţiul ker R al lui K N, se numeşte relaţie de recurenţă liniară omogenă de ordin r Dacă şirurile c 0,, c r K N sunt constante, atunci (17) şi (18) devin c r a n+r + c r 1 a n+r c 0 a n = f (n), n 0 (19) c r a n+r + c r 1 a n+r c 0 a n = 0, n 0 (110) şi se numesc relaţie de recurenţă liniară neomogenă de ordin r cu coeficienţi constanţi respectiv relaţie de recurenţă liniară omogenă de ordin r cu coeficienţi constanţi Cornel Pintea Page 3 of 89 Babeş-Bolyai University 2016
7 Examplul 11 ([2, p62]) Relaţia de recurenţă liniară neomogenă de ordin 1 are soluţia generală a n+1 = c(n)a n + f (n) (111) a n = a 0 c(0) c(n 1) + c(1) c(n 1) f (0) + c(2) c(n 1) f (1) + + c(n 1) f (n 2) + f (n 1) (112) Observăm acum că soluţia generală (112) a relaţiei de recurenţă liniară neomogenă de ordinul 1 (111) are componenta a 0 c(0) c(n 1) care, atunci când a 0 parcurge întregul corp K, generează nucleul ker R al transformării liniare iar şirul (ξ n ) n 0, unde ξ 0 = 0 şi R : K N K N, R(a n ) n 0 = (a n+1 c(n)a n ) n 0, ξ n := c(1) c(n 1) f (0) + c(2) c(n 1) f (1) + + c(n 1) f (n 2) + f (n 1), n 1, este o soluţie particulară a ecuaţiei R(a n ) = f (n), n 0 In termenii aplicaţiei liniare soluţia generală a recurenţei liniare (111) este ker R + (ξ n ) n 0 = (φ n ) n 0 + (ξ n ) n 0, unde φ 0 = 1, iar φ n = c(0) c(n 1) pentru n 1 Dacă şirul (c(n)) este constant şi are termenii egali cu c, atunci relaţia de recurenţă liniară neomogenă de ordin 1 cu coeficienţi constanţi are soluţia generală a n = a 0 c n + a n+1 = ca n + f (n) n 1 c k f (n k 1) k=0 Cornel Pintea Page 4 of 89 Babeş-Bolyai University 2016
8 Teorema 19 ([2, p68]) Dacă s este o rădăcină de ordin m a polinomului c r X r + c r 1 X n+r c 1 X + c 0 C[X], (113) atunci şirurile (n k s n ) n 0, 0 k m 1 sunt soluţii ale relaţiei de recurenţă liniară omogenă de ordin r cu coeficienţi constanţi (110) Dacă c r X r + c r 1 X n+r c 1 X + c 0 = c r (X s 1 ) m1 (X s p ) m p, s i = s j pentru i = j, atunci soluţia generală a recurenţei liniare omogenă de ordin r cu coeficienţi constanţi (110) este mulţimea combinaţiilor liniare a şirurilor (n k s n j ) n 0, 0 k m j 1, 1 l r Aşadar ker R = (s n 1 ), (nsn 1 ),, (nm 1 1 s n 1 ), (sn 2 ), (nsn 2 ),, (nm 1 1 s n 2 ),, (sn p), (ns n 1 ),, (nm p 1 s n p), unde R : K N K N, R(a n ) n 0 = (c r a n+r + c r 1 a n+r c 0 a n ) n 0, iar s 1,, s r sunt rădăcinile polinomului (113), numit polinomul caracteristic al recurenţei liniare omogene de ordin r cu coeficienţi constanţi (110) Prin urmare ker R este un subspaţiu finit dimensional al lui K R şi dim ker R r Examplul 12 Vom determina şirul lui Fibonacci definit de relaţia de recurenţă şi condiţiile iniţiale F 0 = 0 şi F 1 = 1 F n = F n 1 + F n 2 Cornel Pintea Page 5 of 89 Babeş-Bolyai University 2016
9 14 Probleme 1 Se consideră un corp finit K cu card(k) = q (a) Determinaţi numărul punctelor unei varietăţi p-dimensionale ale lui K n (b) Determinaţi numărul dreptelor lui K n care trec printr-un punct fixat 2 În R 4 se dau planul α = (2, 4, 1, 2) + (1, 1, 1, 1), (0, 1, 0, 1) şi dreapta D = (2, 3, 1, 1) + (1, 1, 1, 1) Să se determine D α 3 (A se vedea şi [3, Problema 1, p 91]) Care dintre următoarele submulţimi sunt varietăţi liniare ale spaţiilor lor ambiente? (a) A := {(x 1, x 2, x 3 ) R 3 : 2x 1 x 2 + x 3 2 = 0} (b) B := {(x 1, x 2, x 3 ) R 3 : (x 1 + x 2, 2x 2 + x 3, x 3 2x 1 ) A} (c) C := {(x 1, x 2, x 3 ) R 3 : x 2 1 +x2 2 +x2 3 2x 1x 2 2x 1 x 3 +2x 2 x 3 =0} (d) D := {(x 1, x 2, x 3, x 4 ) R 4 : x x 2 2x 3 + x 4 = 0} 4 Fie a 1, a 2,, a n, b 1, b 2,, b n două şiruri finite de numere reale Fie I R un interval deschis ş g : I R o funcţie de clasă C Care dintre următoarele submulţimi sunt varietăţi liniare ale spaţiului C (I)? (a) A := { f C (I) : f (n) + a 1 f (n 1) + + a n 1 f + a n f + g = 0}; (b) B := {h C (I) : h (n) + b 1 h (n 1) + + b n 1 h + b n h A}; (c) C := {ϕ C (I) : ϕ 3 5ϕ 2 + 6ϕ = 0} Cornel Pintea Page 6 of 89 Babeş-Bolyai University 2016
10 5 ([3, Problema 2, p 91]) În spaţiul R 4 se dau varietăţile liniare Care dintre următoarele relaţii au loc? a = (2, 1, 2, 1), D = (1, 3, 0, 0) + (1, 1, 1, 1) α = (1, 0, 1, 0) + (2, 1, 3, 1), (1, 0, 2, 2) H = (1, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0) a D, a α, a H, D α, D H, α H, D α, α H 6 ([3, Problema 11, p 94]) În spaţiul vectorial V (dim V > 4) se dau trei puncte distincte a, b, c şi un plan α = a + d 1, d 2 Să se determine o varietate liniară 4-dimensională A A(V) care conţine punctele a, b şi c şi este paralel cu α 7 ([3, Problema 13, p 95]) Considerăm un spaţiu vectorial V, o varietate liniară r- dimensională A A(V) şi un punct b V Să se arate că există o singură varietate Cornel Pintea Page 7 of 89 Babeş-Bolyai University 2016
11 liniară r-dimensională B A(V) astfel încât b B şi B A 8 Să se arate că un hiperplan H = a + d 1,, d n 1 a lui R n este caracterizat de ecuaţia x 1 a 1 x 2 a 2 x n a n d 1 1 d 2 1 d n 1 = 0, d 1 n 1 d 2 n 1 d n n 1 unde a = (a 1, a 2,, a n ) şi d i = (d 1 i, d2 i,, dn i ) pentru 1 i n 1 9 Găsiţi soluţia generală a recurenţei liniare neomogene de ordinul 1 cu coeficienţi constanţi a n+1 = ca n + d n Cornel Pintea Page 8 of 89 Babeş-Bolyai University 2016
12 10 Arătaţi că a + ξ 1 η 1 ξ 1 η 2 ξ 1 η m ξ 2 η 1 a + ξ 2 η 2 ξ 2 η m ξ m η 1 ξ m η 2 a + ξ m η m = a m 1 (a + ξ 1 η ξ m η m ) (114) Indicaţie Arătaţi mai întâi că determinatul de mai sus, sa-i spunem m, satisface relaţia de recurenţă m = a m 1 + ξ m η m a m 1 11 Determinaţi şirul (a n ) dat prin relaţia de recurenţă a n+2 = 2(a n+1 a n ) şi prin condiţiile iniţiale a 0 = a 1 = 1 12 Determinaţi, în funcţie de a 0 şi a 1 şirul dat prin relaţia de recurenţă liniară a n+2 (s 1 + s 2 )a n+1 + s 1 s 2 a n = 0 Cornel Pintea Page 9 of 89 Babeş-Bolyai University 2016
13 13 Dacă (F n ) notează şirul lui Fibonacci (definit de relaţia de recurencţă F n = F n 1 + F n 2 şi condiţiile iniţiale F 0 = 0 şi F 1 = 1), arătaţi că F lim n+1 = n F n 2 Cornel Pintea Page 10 of 89 Babeş-Bolyai University 2016
14 2 Săptămâna 2 21 Învelitori şi combinaţii afine Definiţia 21 Dacă M este o submulţime a lui V, atunci varietatea liniară af(m) := {A M A, A A(V)} se numeşte înfăşurătoarea sau anvelopa sau închiderea afină a lui M Propoziţia 21 (Proprietăţile operatorului af ) Fie M, N P(V) şi A A(V) 1 M af(m) şi af(m) A(V) 2 Dacă M A şi A A(V), atunci af(m) A 1 3 M N = af(m) af(n) 2 4 af(m) = M M A(V) 5 af (af(m)) = af(m) 3 În secţiunea următoare vom arăta că învelitoarea afină a mulţimii M este mulţimea combinaţiilor afine de elemente din M Definiţia 22 O combinaţie liniară m m λ i x i aî λ i = 1, se numeşte combinaţie afină i=1 i=1 Propoziţia 22 O submulţime L a lui V este varietate liniară a lui V dacă şi numai dacă ( ) m m x 1,, x m L şi λ 1,, λ m K, λ i = 1 λ i x i L (21) i=1 i=1 1 af(m) este cea mai mică varietate liniară ce conţine mulţimea M 2 Operatorul af este crescător 3 Operatorul af este idempotent Cornel Pintea Page 11 of 89 Babeş-Bolyai University 2016
15 Propoziţia 23 Dacă M P(V), atunci { m m af(m) = λ i x i N, xi M, λ i K, i =1,, m, i=1 m i=1 } λ i = 1 22 Dreptele unui spaţiu afin Amintim că dacă a şi b sunt puncte distincte în V, atunci există o singură dreaptă, notată cu ab, care conţine pe a şi b Mai precis ab = a + b a Cornel Pintea Page 12 of 89 Babeş-Bolyai University 2016
16 Propoziţia 24 Fie V un spaţiu vectorial cu scalari într-un corp K cu cel puţin 3 elemente O submulţime L a lui V este varietate liniară dacă şi numai dacă, odată cu două puncte distincte a, b L, mulţimea L conţine întreaga dreaptă ab Demonstraţie Avem de arătat că L A(V) (x, y L, t K = (1 t)x + ty L) = Din x, y L deducem că y L = x + D(L), adică y x D(L) şi implicit că y x D(L) Aşadar xy = x + y x x + D(L) = L = Putem presupune că L = deoarece, altfel n-am avea nimic de demonstrat Considerăm a L şi arătăm că Y = L a este un subspaţiu vectorial al lui V Pentru aceasta considerăm y 1 = x 1 a, y 2 = x 2 a Y, unde x 1, x 2 L Dacă t K, atunci observăm că (1 t)y 1 + ty 2 = (1 t)x 1 + tx 2 (1 t)a ta = (1 t)x 1 + tx 2 a, care conform ipotezei în care lucrăm, aparţine lui L a = Y Am arătat deci că Luând y 1 = 0 obţinem că y 1, y 2 T, t K = (1 t)y 1 + ty 2 Y (22) y Y, t K = ty Y Fie acum α K \ {0, 1}, adică α şi 1 α sunt inversabile Aşadar (1 α) 1 y 1 Y şi α 1 y 2 Y pentru orice y 1, y 2 Y, fapt care arată, folosind (22), că Aşdar Y V şi L = a + Y y 1 + y 2 = (1 α)[(1 α) 1 y 1 ] + α[α 1 y 2 ] Y Examplul 21 Dacă corpul K al scalarilor lui V are doar două elemente, atunci propoziţia 24 nu are loc Într-adevăr, dacă K = Z 2 = {ˆ0, ˆ1}, atunci submulţimea M := {(ˆ0, ˆ0), (ˆ0, ˆ1), (ˆ1, ˆ0)} a planului V = Z 2 2 conţine toate dreptele care trec prin câte două puncte din M, întrucât dreptele planului Z 2 2 sunt formate din doar două puncte, şi totuşi M nu este varietate liniară Într-adevăr, dacă M ar fi varietate liniară a lui V, atunci M ar fi chiar subspaţiu vectorial al lui V deoarece 0 M Dar atunci (ˆ1, ˆ1) = (ˆ0, ˆ1) + (ˆ1, ˆ0) ar aparţine lui M, ceea ce nu este adevărat Observaţia 21 Propoziţia (24) poate fi rescrisă în termenii aplicaţiei α : P(V) P(V), α(m) = {tx + (1 t)y x, y M, t K} (23) astfel: Fie V un spaţiu vectorial cu scalari într-un corp K cu cel puţin 3 elemente O submulţime L a lui V este varietate liniară dacă şi numai dacă α(l) L Observaţia 22 Fie V un spaţiu vectorial cu scalari într-un corp K Dacă M V, atunci M α(m) α 2 (M) af(m) Într-adevăr, incluziunea M α(m) este evidentă, fapt care arată că M α(m) α 2 (M) α k (M) (24) Din relaţia M af(m) deducem α(m) α(af(m)) af(m), precum şi că α k (M) af(m), pentru orice k 1 O întrebare naturală care apare în legătură cu şirul (24) este dacă termanii acestuia acoperă întrega învelitoare afină a lui M începând cu un anumit rang Dacă spaţiul ambiant V a lui M este finit-dimensional, atunci răspunsul este afirmativ, aşa cum vom vedea mai târziu Cornel Pintea Page 13 of 89 Babeş-Bolyai University 2016
17 23 Probleme 1 Să se arate că două varietăţi liniare r-dimensionale A şi B ale unui spaţiu vectorial V sunt paralele dacă şi numai dacă D(A) = D(B) 2 In R 4 considerăm următoarele varietăţi liniare { x1 + x (L 1 ) 3 2 = 0 2x 1 x 2 + x 3 + 3x 4 1 = 0 (L 2 ) x 1 + x 2 + 2x 3 3x 4 = 1 x 2 + x 3 3x 4 = 1 x 1 x 2 + 3x 4 = 3 (a) Să se determine dimensiunile lui L 1 şi L 2 şi să se scrie ecuaţiile lor paramertice şi vectoriale (b) Să se arate că L 1 L 2 3 În spaţiul afin R n (n 2) se dau dreapta = (a 1,, a n ) + (p 1,, p n ), (p p2 n > 0) şi hiperplanul H : α 1 x α n x n + β = 0, (α α2 n > 0) Să se arate că H dacă şi numai dacă α 1 p α n p n = 0 Cornel Pintea Page 14 of 89 Babeş-Bolyai University 2016
18 4 Să se arate că pentru orice submulţimi M şi N ale spaţiului vectorial V are loc relaţia af (af(m) af(n)) = af(m N) (25) Cornel Pintea Page 15 of 89 Babeş-Bolyai University 2016
19 3 Săptămâna 3 Observaţia 31 Dacă V este un spaţiu vectorial n-dimensional şi M V este o mulţime nevidă, atunci af(m) = { m m } 1 λ i x i m n + 1, λi K, x i M, i = 1, m, λ i = 1 i=1 i=1 31 Teorema dimensiunii Paralelism Propoziţia 31 Dacă A, B A(V), a A, b B, atunci af(a B) = a + D(A) + D(B) + b a Propoziţia 32 Fie A, B A(V), a A, b B Atunci A B = b a D(A) + D(B) Cornel Pintea Page 16 of 89 Babeş-Bolyai University 2016
20 Propoziţia 33 Dacă varietăţile liniare A şi B au un punct comun a, atunci avem af(a B) = a + D(A) + D(B) şi A B = a + D(A) D(B) Examplul 31 Dacă A, B sunt varietăţi liniare într-un spaţiu vectorial peste K Z 2 şi A B =, atunci af(a B) = {ta + (1 t)b a A, b B, t K} (31) Ipotezele A B = şi K Z 2 sunt esenţiale Observaţia 32 Fie V un spaţiu vectorial peste corpul K 1 Dacă A, B A(V) sunt varietăţi liniare astfel încât A B =, atunci se poate uşor arăta că α(a B) = {λa + (1 λ)b a A, b B, λ K}unde α este funcţia (23) Egalitatea 31) ne arată că pentru M = A B invelitoarea afină af(m) = af(a B) este acoperită de la prima iterare α(m), adică egalitatea af(m) = α r (M) are loc pentru r = 1 2 Dacă A este o varietate liniară a spaţiului vectorial V de dimensiune cel puţin unu şi c V \ A un punct dat, atunci α({c} A) = a A af(a, c) Faptul că α({c} A) = a A af(a, c) nu este o varietate liniară (a se vedea problema 32(1)) arată că egalitatea α r ({c} A) = af({c} A) este satisfăcută pentru r 2 Se poate arăta că α 2 ({c} A) = af({c} A) în cazul K = Z2 Teorema 34 (Teorema dimensiunii) Fie A, B varietăţi liniare nevide de finit dimensionale Cornel Pintea Page 17 of 89 Babeş-Bolyai University 2016
21 1 Dacă A B =, atunci dim af(a B) = dim(a) + dim(b) dim(a B) 2 Dacă A B =, atunci dim af(a B) = dim (D(A) + D(B)) + 1 Propoziţia 35 Presupunem că dim(v) = n Dacă varietatea afină A A(V) nu are niciun punct comun cu hiperplanul H, atunci A H Observaţia 33 Dacă dreapta L intersectează hiperplanul H într-un punct, atunci orice dreaptă paralelă L la L intersectează H tot într-un punct Într-adevăr, altfel am avea L H, adică L H şi deci L H sau L H = 32 Probleme 1 Fie A o varietate liniară de dimensiune cel puţin unu a unui spaţiu vectorial V şi c V \ A un punct dat Este mulţimea o varietate liniară? a A af(a, c) 2 Să se arate că dacă în structura afină a unui spaţiu vectorial 4-dimensional două hiperplane au un punct comun, atunci ele au un plan comun 3 Se consideră varietăţile liniare A şi B astfel încât A B = şi dim A = dim B = p Să se arate că A B dacă şi numai dacă A şi B sunt incluse într-o varietate de dimensiune p + 1 Cornel Pintea Page 18 of 89 Babeş-Bolyai University 2016
22 4 Se consideră în R 5 vectorii a = (1, 0, 0, 2, 0), b = (0, 2, 0, 0, 1), c = (1, 2, 0, 0, 0) şi d = (0, 0, 0, 2, 1) şi varietăţile liniare A = a + b, c, B = c + b, d Să se afle A B şi af(a B) 5 Fie V un spaţiu vectorial finit dimensional peste corpul K, unde K Z 2 Se consideră aplicaţia α : P(V) P(V), α(m) = {tx + (1 t)y x, y M, t K} şi iteratele α 1 = α, α 2 = α α, Să se arate că pentru orice M P(V) se poate găsi un număr natural r astfel încât af(m) = α r (M) Să se arate că ipoteza K Z 2 este esenţială Cornel Pintea Page 19 of 89 Babeş-Bolyai University 2016
23 6 Să se determine toate poziţiile reciproce posibile a două plane α şi β dintr-un spaţiu vectorial 4-dimensional precizând în fiecare caz şi dim(af (α β)) 7 Într-un spaţiu vectorial n-dimensional fie L 1 şi L 2 două varietăţi liniare de dimensiune p respectiv q (p > q, p + q n 1), astfel încât L 1 L 2 = şi L 1 L 2 Să se determine mulţimea valorilor posibile pentru dim af(l 1 L 2 ) 8 În structura afină a unui spaţiu vectorial n-dimensional considerăm două hiperplane Care sunt valorile posibile pentru dim(h 1 H 2 ) şi dim af(h 1 H 2 )? Cornel Pintea Page 20 of 89 Babeş-Bolyai University 2016
24 9 În structura afină a unui spaţiu vectorial n-dimensional se consideră un hiperplan H şi o varietate lininară p-dimensională (p < n 1) Să se arate că atunci are loc una dintre relaţiile: (a) dim(h A p ) = p 1; (b) H A p Cornel Pintea Page 21 of 89 Babeş-Bolyai University 2016
25 4 Săptămâna 4: Proprietăţi laticeale Mulţimi convexe 41 Proprietăţi laticeale ale structurii afine Teorema 41 Structura afină A(V) este o latice completă Pentru o familie oarecare {A i } i I de varietăţi liniare ale lui V avem: inf A i = A i şi sup A i = af ( ) A i i I i I i I i I Observaţia 41 1 Dacă A, B A(V) şi a A, b B, atunci A B = a + D(A) + D(B) + b a şi A B = A B 2 Dacă A B = şi a A B, atunci A B = a + D(A) + D(B) şi A B = A B = a + D(A) D(B) Propoziţia 42 Dacă spaţiile vectoriale V şi W, având scalarii în acelaşi corp K, sunt izomorfe, atunci laticele A(V) şi A(W) sunt izomorfe Dacă f : V W este un izomorfism liniar, atunci aplicaţia f : A(V) A(W), f (A) := { f (a) a A} = f (A) este un izomorfism laticeal 42 Structura afină a spaţiului vectorial K n Din Propoziţia 42 reiese importanţa structurii afine A(K n ) a lui K n Într-adevăr, orice spaţiu vectorial n-dimensional peste K este izomorf cu K n, structurile afine ale spaţiilor vectoriale n-dimensionale fiind laticeal izomorfe cu A(K n ) Fie A = x 0 + D(A) A(K n ), iar {d 1,, d r } o bază a lui D(A), x 0 = (x 1,, x n ) şi d j = (d 1j,, d nj ), j = 1, 2,, r Aşadar Relaţiile A = { (x 1,, x n ) K n x i = xi 0 r } + d ij λ j, λ j K j=1 x i = x 0 i + r d ij λ j, i = 1,, n (41) j=1 se numesc ecuaţiile parametrice ale varietăţii liniare A Pe de altă parte, varietăţile liniare ale lui K n coincid cu soluţiile sistemelor liniare Mai precis, orice varietate liniară A A(K n ) poate fi caracterizată şi astfel: A = { (x 1,, x n ) K n Condiţiile care figurează aici, adică n } a ij x j = b i, i = 1,, m j=1 n a ij x j = b i, i = 1,, m, j=1 se numesc ecuaţiile implicite ale varietăţii liniare A Intersecţia a două varietăţi liniare A, B A(K n ) se caracterizează uşor dacă A şi B sunt date prin sisteme de ecuaţii Mai precis sistemul de ecuaţii a lui A B se obţine luând ecuaţiile lui A şi B Varietatea liniară A B, subîntinsă de varietăţile liniare A şi B, se caracterizează însă mai uşor dacă avem reprezentările parametrice ale varietăţilor A şi B Cornel Pintea Page 22 of 89 Babeş-Bolyai University 2016
26 43 Submulţimile convexe ale unui spaţiu vectorial real Definiţia 41 Fie V un spaţiu vectorial real O mulţime C V se numeşte convexă dacă pentru orice x, y C segmentul [xy] := {(1 t)x + ty : t [0, 1]} este conţinut în C Definiţia 42 Dacă M este o submulţime a lui V, atunci mulţimea conv(m) := {C M C şi C convexă} se numeşte învelitoarea convexă sau închiderea convexă a lui M Propoziţia 43 (Proprietăţile operatorului conv) 1 M conv(m) şi conv(m) este o mulţime convexă pentru orice M P(V) 2 Dacă M C şi C este convexă, atunci conv(m) C 4 3 M N = conv(m) conv(n) 5 4 conv(m) = M dacă şi numai dacă M este convexă 5 conv (conv(m)) = conv(m) pentru orice M P(V) 6 Observaţia 42 1 Dacă {C i } i I este o familie de submulţimi convexe ale spaţiului vectorial real V, atunci intersecţia C i este de asemenea o mulţime convexă i I 2 Submulţimea M a spaţiului vectiral real V este convexă dacă şi numai dacă m 1, x 1,, x m, t 1,, t m [0, 1], t t m = 1 t 1 x t m x m M Definiţia 43 O combinaţie liniară combinaţie convexă m λ i x i aî i=1 m λ i = 1 şi λ 1,, λ m [0, 1], se numeşte i=1 Propoziţia 44 Dacă V este un spaţiu vectorial real şi M V este o mulţime nevidă, atunci conv(m) = { m m λ i x i 1, xi M, λ i [0, 1], i = 1, m, i=1 m } λ i = 1 i=1 4 conv(m) este cea mai mică mulţime convexă ce conţine mulţimea M 5 Operatorul conv este crescător 6 Operatorul conv este idempotent Cornel Pintea Page 23 of 89 Babeş-Bolyai University 2016
27 431 Teorema lui Carathéodory Teorema 45 (Carathéodory) Dacă V este un spaţiu vectorial real n-dimensional şi M V este o mulţime nevidă, atunci conv(m) = { m 1 λ i x i m n + 1, xi M, λ i [0, 1], i = 1, m, i=1 m } λ i = 1 i=1 44 Probleme 1 Dacă C 1, C 2 sunt două submulţimi convexe ale lui R n, ară taţi că C 1 + C 2 este de asemenea convexă 2 În spaţiul vectorial R 2 vârfurile unui triunghi sunt A 1 (x 1, y 1 ), A 2 (x 2, y 2 ), A 3 (x 3, y 3 ) Să se arate că punctul M(x, y) este în interiorul triunghiului A 1 A 2 A 3 dacă şi numai dacă S 12 (x, y)s 12 (x 3, y 3 ) > 0, S 23 (x, y)s 23 (x 1, y 1 ) > 0, S 31 (x, y)s 31 (x 2, y 2 ) > 0, unde S ij (x, y) = x y 1 x i y i 1 x j y j 1 Cornel Pintea Page 24 of 89 Babeş-Bolyai University 2016
28 3 Fie A, B R n mulţimi convexe disjuncte şi nevide, iar x un punct din R n Arătaţi că conv({x} A) = {ta + (1 t)x a A, t [0, 1]} Arătaţi că A conv({x} B) = sau B conv({x} A) = 4 Să se arate că pentru două submulţimi oarecare A şi B ale lui R n are loc egalitatea: conv(a) + conv(b) = conv(a + B) Cornel Pintea Page 25 of 89 Babeş-Bolyai University 2016
29 5 Să se arate că rădăcinile polinomului derivat al unui polinom neconstant cu coeficienţi complecşi aparţin învelitorii convexe a rădăcinilor polinomului dat (Teorema Gauss-Lucas) Cornel Pintea Page 26 of 89 Babeş-Bolyai University 2016
30 5 Săptămâna 5 Teoremele lui Radon, Helly, Minkowsky, Krein-Milman şi Motzkin 51 Teorema lui Radon Teorema 51 (Radon) Dacă M este submulţime finită a unui spaţiu vectorial real n-dimensional formată din m n + 2 puncte, atunci există submulţimile disjuncte M 1, M 2 ale lui M astfel încât M = M 1 M 2 şi conv(m 1 ) conv(m 2 ) = 52 Teorema lui Helly Teorema 52 (Helly) Dacă submulţimile convexe M 1,, M r ale spaţiului afin R n sunt astfel încât r n + 1 şi, luate câte n + 1 în toate modurile posibile, au intersecţia nevidă, atunci M 1 M r = Cornel Pintea Page 27 of 89 Babeş-Bolyai University 2016
31 53 Teoremele lui Minkowski, Krein-Milman şi Motzkin Definiţia 51 Un punct extremal al mulţimii convexe C este un punct x C cu următoarea proprietate λy + (1 λ)z = x, y, z C, λ (0, 1) = y = z = x Teorema 53 (Minkowski) Orice submulţime convexă şi compactă a lui R n este închiderea convexă a mulţimii punctelor sale extremale Teorema 54 (Krein-Milman) Orice submulţime convexă şi compactă K a unui spaţiu local convex poate fi reprezentată sub forma K = cl conv ext K, unde ext K este mulţimea punctelor extremale ale lui K Teorema 55 (Motzkin) Orice mulţime poliedrală este suma (Minkowski) dintre un politop şi un con convex 54 Probleme 1 Găsiţi o familie (infinită) de mulţimi convexe din plan având intersecţia vidă, iar intersecţia oricăror 3 mulţimi din familie este nevidă 2 Se consideră înplan o mulţime finită cu proprietatea că oricare trei puncte ale mulţimii sunt conţinute într-un disc de rază 1 Să se arate că există un disc de rază 1 care conţine toate punctele mulţimii date Cornel Pintea Page 28 of 89 Babeş-Bolyai University 2016
32 3 Considerăm în plan n segmente paralele astfel în cât pentru oricare 3 dintre ele există o dreaptă care le intersectează Să se arate că există o dreaptă care intersectează toate segmentele 4 Considerăm în plan n segmente paralele astfel în cât pentru oricare 4 dintre ele există o parabolă care le intersectează Să se arate că există o parabolă care intersectează toate segmentele 5 (Jung) Să se arate că orice mulţime finită din plan de diametru 1 poate fi acoperită de un disc de rază 1 3 Cornel Pintea Page 29 of 89 Babeş-Bolyai University 2016
33 Cornel Pintea Page 30 of 89 Babeş-Bolyai University 2016
34 6 Săptămâna 6: Spaţiul afin 61 Definiţie şi exemple Definiţia 61 Se numeşte spaţiu afin un triplet (X, X, ϕ), unde X este o mulţime ale cărei elemente se numesc puncte, X este un spaţiu vectorial, iar ϕ : X X X este o aplicţie a î: 1 ϕ(p, Q) + ϕ(q, R) = ϕ(p, R), P, Q, R X 2 Pentru orice O X şi orice a X, există un singur punct A X astfel ca ϕ(o, A) = a Cu notaţia PQ:= ϕ(p, Q), condiţiile de mai sus se scriu: 1 PQ + QR= PR, P, Q, R X 2 Pentru orice O X aplicaţia ϕ O : X X definită prin ϕ O (M) = OM este bijectivă Luând P = Q = R = A în (1 ) deducem AA= 0, A X Examplul 61 1 Tripletul (P, V, ϕ), unde ϕ : P P V, ϕ(a, B) = AB este un spaţiu afin 2 Tripletul (V, V, ϕ), unde V este un spaţiu vectorial şi ϕ : V V V, ϕ(v 1, v 2 ) = v 2 v 1, este un spaţiu afin Întrucât ϕ O : X X este bijecţie, iar X este un spaţiu vectorial, există o unică structură de spaţiu vectorial pe X astfel încât ϕ O este izomorfism Această structură este dată de operaţiile: 1 P = A O B OP= OA + OB 2 Q = λ O A OQ= λ OA, iar spaţiul vectorial (X, O, O ) se notează cu T O (X) şi se numeşte spaţiul vectorial tangent la X în punctul O Menţionăm că structura lui X dată de operaţiile O şi O depinde de alegerea punctului O Cu toate acestea mulţimea varietăţilor liniare ale lui T O (X) nu depinde de O X Cornel Pintea Page 31 of 89 Babeş-Bolyai University 2016
35 62 Subspaţii afine Întrucât ϕ O : X X este bijecţie, iar X este un spaţiu vectorial, există o unică structură de spaţiu vectorial pe X astfel încât ϕ O este izomorfism Această structură este dată de operaţiile: 1 P = A O B OP= OA + OB 2 Q = λ O A OQ= λ OA, iar spaţiul vectorial (X, O, O ) se notează cu T O (X) şi se numeşte spaţiul vectorial tangent la X în punctul O Menţionăm că structura lui X dată de operaţiile O şi O depinde de alegerea punctului O Cu toate acestea mulţimea varietăţilor liniare ale lui T O (X) nu depinde de O X Propoziţia 61 Varietăţile liniare nevide ale lui T O (X) sunt submulţimile lui X de forma unde A X şi U X L = {M AM U}, (61) Observaţia 61 În egalitatea 61 punctul A L poate fi ales arbitrar în L, iar subspaţiul U al lui X este unic determinat de L şi U = { AM M L} Definiţia 62 Se numeşte varietate liniară sau subspaţiu afin al lui X orice varietate liniară a spaţiului vectorial T O (X) Mulţimea varietăţilor liniare ale lui X se notează cu A(X) Spaţiul director al varietăţii liniare L A(X) este spaţiul director al varietăţii liniare ϕ O (L), adică { AM: M L} 63 Combinaţii afine în spaţii afine Fie (X, X, ϕ) un spaţiu afin şi A 1,, A m X, iar λ 1,, λ m scalari daţi Punctul M = λ 1 O A 1 O O λ m O A m (62) este doar atunci definit când s-a ales un punct O X, iar M depinde de alegerea lui O m Dacă însă combinaţia liniară 62 este o combinaţie afină, adică λ i = 1, atunci punctul M nu i=1 depinde de alegerea punctului O X Cornel Pintea Page 32 of 89 Babeş-Bolyai University 2016
36 Definiţia 63 Date fiind punctele A 1,, A m X şi scalarii λ 1,, λ m astfel încât m i=1 λ i = 1, punctul M definit prin relaţia 62 se numeşte baricentrul sistemului de puncte A 1,, A m cu ponderile λ 1,, λ m Propoziţia 62 Fie (X, X, ϕ) un spaţiu afin şi S X; atunci S este un subspaţiu afin al lui X dacă şi numai dacă pentru orice sistem finit de puncte din S, orice baricentru al acestui sistem aparţine lui S Propoziţia 63 Fie A 0, A 1,, A m puncte ale spaţiului afin X Atunci M af{a 0, A 1,, A m } A 0 M A 0 A 1,, A 0 A m Corolarul 64 dim af{a 0, A 1,, A m } m Corolarul 65 Următoarele afirmaţii sunt echivalente: 1 dim af{a 0, A 1,, A m } = m 2 vectorii A 0 A 1,, A 0 A m sunt liniar independenţi 3 nici unul dintre punctele A 0, A 1,, A m nu aparţine subspaţiului afin subîntins de celelalte Definiţia 64 Punctele A 0, A 1,, A m se numesc afin independente dacă ele îndeplinesc una dintre condiţiile corolarului 65 În caz contrar aceste puncte se numesc afin dependente 64 Repere afine şi repere carteziene Definiţia 65 Un sistem de puncte A 0, A 1,, A n afin independente, luate într-o ordine determinată, se numeşte reper afin al varietăţii liniare L = af{a 0, A 1,, A n } De exemplu punctele A 0 = (0,, 0), A i = (δi 1,, δn i ), unde δj i este simbolul lui Kronecker, i = 1,, n formează un reper afin al lui K n Fie A 0, A 1,, A n un reper afin al lui L A(X) Dat fiind M L, există scalarii ξ 0, ξ 1,, ξ n astfel încât, pentru orice O X să avem: OM= OA i şi particular A 0 M= n ξ i i=0 A 0 A i = n i=1 ξ i A 0 A i, deoarece A 0 A 0 = 0 n ξ i i=0 n ξ i = 1 În i=0 A 0 A n sunt liniar independenţi, rezultă că scalarii ξ 1,, ξ n, Întrucât vectorii A 0 A 1,, şi prin urmare ξ 0 = 1 ξ 1 ξ n, cu proprietăţile de mai sus sunt unici Scalarii ξ 0, ξ 1,, ξ n se numesc coordonatele baricentrice ale lui M, iar ξ 1,, ξ n se numesc coordonatele carteziene ale lui M faţă de reperul afin (A 0, A 1,, A n ) Cornel Pintea Page 33 of 89 Babeş-Bolyai University 2016
37 Definiţia 66 Se numeşte reper cartezian al varietăţii liniare L A(X) orice pereche R = (O, b), unde O L, iar b = [e 1,,e n ] este o bază ordonată a spaţiului director L Punctele (O, A 1,, A n ) cu proprietatea că e i = OA i, i = 1,, n formează reperul afin asociat reperului cartezian R Fie R = (O, e 1,, e n ) un reper cartezian al spaţiului afin X Vom folosi notaţiile [M] R = [ OM] b = ξ 1 ξ n sau M(ξ 1, ξ n ) Observăm că dacă [M] R = [ξ i ] şi [N] R = [η i ], atunci componentele vectorului MN faţă de baza b sunt η i ξ i, adică [ MN] b = [η i ξ i ], întrucât MN= ON OM Dacă (A 0, A 1,, A n ) este un reper afin al spaţilui afin X, atunci aplicaţia T A 0 (X) Kn, M(x 1,, x n ) (x 1, x n ) defineşte un izomorfism de spaţii vectoriale, care determină, la rândul său, un izomorfism laticeal A(X) A(K n ) Teorema 66 Fie R = (O, b) un reper cartezian al spaţilui afin X şi (x 1,, x n ) coordonatele uni punct generic al spaţiului X faţă de acest reper Atunci o varietate liniară r-dimensională se caracterizează prin ecuaţii parametrice de forma x i = x 0 i + r d ij λ j, i = 1,, n j=1 O varietate liniară (n m)-dimensională se identifică cu mulţimea soluţiilor unui sistem de ecuaţii liniare n a ij x j = b i, i = 1,, m j=1 65 Schimbarea coordonatelor Fie R = (O, b) şi R = (O, b ) două repere carteziene ale lui X şi T matricea de trecere de la bază b la baza b Pentru a stabili legătura dintre [M] R şi [M] R observăm că avem succesiv: [M] R = [ OM] b = T [ OM] b = T [ OO + O M] b = T [ O M] b + T [ OO ] b = T [M] R + [ OO ] b = T [M] R + [O ] R Propoziţia 67 Schimbarea coordonatelor carteziene se face după formula [M] R = T [M] R + [O ] R În termenii coordonatelor carteziene formula schimbării de coordonate devine x i = unde T = (t ij ) şi [O ] t R = (α 1 α n ) n t ij x j + α i, i = 1,, n, i=0 Cornel Pintea Page 34 of 89 Babeş-Bolyai University 2016
38 66 Probleme 1 În spaţiul vectorial K n, unde K este un corp oarecare, se consideră o varietate liniară p- dimensională A Să se construiască o aplicaţie ϕ : A A K p astfel încât (A, K p, ϕ) să fie un spaţiu afin 2 Fie A, B două puncte ale unui spaţiu afin real X şi C, D punctele definite prin C = 1 1 λ A + λ λ 1 B, D = λ A + λ λ + 1 B, unde λ R \ { 1, 1} Arătaţi că EA= λ 2 EB, unde E = 1 2 C D 3 Fie A 1,, A n puncte ale spaţiului afin real X şi λ 1,, λ n scalari reali astfel încât n λ i = 1 Considerăm punctele i=1 B 1 = λ 1 A 1 + λ 2 A λ n 1 A n 1 + λ n A n B 2 = λ 1 A 2 + λ 2 A λ n 1 A n + λ n A 1 B 3 = λ 1 A 3 + λ 2 A λ n 1 A 1 + λ n A 2 B n 1 = λ 1 A n 1 + λ 2 A n + + λ n 1 A n 3 + λ n A n 2 B n 1 = λ 1 A n + λ 2 A λ n 1 A n 2 + λ n A n 1 Arătaţi că cele două sisteme de puncte au acelaşi centru de greutate 7, adică 1 n A n A n A n = 1 n B n B n B n (63) 7 Centrul de greutate al unui sistem de puncte A 1,, A n dintr-un spaţiu afin X este baricentrul sitemului cu ponderi egale G = 1 n A n A n A n Cornel Pintea Page 35 of 89 Babeş-Bolyai University 2016
39 4 Fie A 1,, A n, B 1,, B n puncte din spaţiul afin real X Arătaţi că unde A 1 B A n B n = n GG, G = 1 n A n A n A n, G = 1 n B n B n B n sunt centrele de greutate ale celor două sisteme de puncte Prin urmare cele două sisteme de puncte au acelaşi centru de greutate ddacă A 1 B A n B n = 0 5 Se consideră un reper afin (A 0, A 1,, A n ) al spaţiului afin X şi baricentrele de ponderi egale 8 n 1 Gi = n A j j=0,j =i 8 Centrele de greutate ale feţelor simplexului A 0 A 1 A n Cornel Pintea Page 36 of 89 Babeş-Bolyai University 2016
40 Să se arate că n i=0 A i G i = {G}, unde G = 1 n + 1 A n + 1 A n + 1 A n, adică intersecţia dreptelor A i G i, i {0, 1, n} este centrul de greutate al sistemului de puncte A 0, A 1,, A n 6 Într-un spaţiu afin tridimensional raportat la reperul cartezian R = (O, e 1, e 2, e 3 ) se dau punctele O (0, 3, 1) şi vectorii e 1 (2, 1, 1), e 2 (2, 1, 2), e 3 (3, 0, 1) Să se scrie formulele de trecere de la reperul R la reperul R = (O, e 1, e 2, e 3 ) Să se determine coordonatele punctului A(1, 2, 0) faţă de reperul R 7 În planul afin K 2 considerăm un repoer afin R = (A 0, A 1, A 2 ) (a) Care sunt coordonatele lui A 1 faţă de R? Cornel Pintea Page 37 of 89 Babeş-Bolyai University 2016
41 (b) Să se scrie ecuaţia dreptei AB, unde A, B K 2, unde [A] R = [ a 0 ] [ 0, [B] R = b ] (c) Să se calculeze coordonatele punctelor A 0, A şi B faţă de reperul R = (A 1, A 2, A 3 ), unde [ ] [A 3 1 ] R = 1 8 În spaţiul afin 4-dimensional X raportat la reperul cartezian R = (A 0, A 0 A 1, se dau puntele B(1, 1, 0, 0), C(0, 1, 1, 0) (a) Să se arate că este un reper cartezian R = (A 3, A 3 A 1, A 0 A 2, A 0 A 3, A 3 A 4, A 3 B, A 0 A 4 ) A 3 A 2 ) (b) Să se scrie formulele de trecere de la reperul R la reperul R (c) Să se determine [M] R şiind că [M] = [ ] t R (d) Un subspaţiu afin al lui X este dat, faţă de reperul R, prin sistemul { x1 + 2x 2 x 3 = 0 x 1 +x 4 = 2 Care sunt ecuaţiile acestui subspaţiu faţă de reperul R? Cornel Pintea Page 38 of 89 Babeş-Bolyai University 2016
42 (e) Un subspaţiu afin al lui X este dat, faţă de reperul R, prin sistemul { x1 x 2 + x 3 x 4 = 0 x 2 + x 3 = 5 Care sunt ecuaţiile acestui subspaţiu faţă de reperul R? 9 Se consideră un plan π şi R = (O, i, j ) un reper cartezian ortonormat al său Considerăm de asemenea elipsa E a cărei ecuaţie faţă de reprerul cartezian ortonormat R = (O, ( i, j ) este 10x 2 + 5y 2 = 10, unde O 4 5, 2 ) şi 2 i = 5 i 1 j şi 5 5 Cornel Pintea Page 39 of 89 Babeş-Bolyai University 2016
43 j = 1 5 i j Aflaţi ecuaţia elipsei E faţă de reperul R 10 Se consideră un plan π şi R = (O, i, j ) un reper cartezian ortonormat al său Considerăm de asemenea hiperbola H a cărei ecuaţie faţă de reprerul cartezian ortonormat R = (O, i, j ) este 4x 2 y 2 = 36, unde O (3, 4) şi 1 i = 5 i + 2 j şi 5 j = 2 5 i j Aflaţi ecuaţia hiperbolei H faţă de reperul R Cornel Pintea Page 40 of 89 Babeş-Bolyai University 2016
44 7 Săptămâna 7 71 Funcţii polinomiale 711 Definiţii şi observaţii Fie X un spaţiu afin real n-dimensional O funcţie f : X R se numeşte funcţie polinomială dacă există un reper cartezian R = (O, e 1,, e n ) al lui X şi un polinom F R [ X 1, X 2,, X n ] astfel încât pentru orice punct X X de coordonate carteziene (x1, x 2,, x n ) faţă de R să avem f (X) = F(x 1, x 2,, x n ), adică f este un polinom în coordonatele lui X faţă de R Observăm că noţiunea de funcţie polinomială nu depinde de alegerea reperului cartezian R Întradevăr, dacă S este un alt reper cartezian şi f : X R este un polinom în coordonatele lui X faţă de R, atunci f este un polinom de acelaşi grad şi în coordonatele lui X faţă de S, deoarece formulele de trecere de la reperul R la reperul S sunt polinoame de gradul întâi reversibile Prin urmare gradul polinomului F este invariant la schimbarea reperului şi se numeşte gradul lui f Alegerea convenabilă a reperului poate conduce la o formă cât mai simplă a polinomului de reprezentare a lui f Definiţia 71 Dacă f : X R este o funcţie polinomială de gradul doi pe spaţiul afin n-dimensional X, atunci preimaginea Q = f 1 (0) se numeşte hipercuadrică Dacă n = 2, atunci Q se numeşte conică, iar dacă n = 3, atunci Q se numeşte cuadrică 712 Funcţii polinomiale de gradul doi Reprezentări matriceale Fie f : X R este o funcţie polinomială de gradul doi care, faţă de reperul cartezian n n R = (O, e 1,, e n ) al lui X, are reprezentarea f (M) = a a i0 x i + a ij x i x j pentru i=1 i,j=1 orice M(x 1,, x n ) X Aceasta se poate reprezentă matriceal astfel: f (M) = a (a 10 a n0 )[M] R + [M] t R A[M] R, unde A := a 11 a 12 a 1n a 21 a 22 a 2n a n1 a n2 a nn Matricea A poate fi aleasă simetrică deoarece f admite şi reprezentarea f (M) = a (a 10 a n0 )[M] R + [M] t A + A t [M] R 2 R Notăm cu [ f ] R matricea A, atunci când A este simetrică, adică f (M) = a (a 10 a n0 )[M] R + [M] t [ f ] [M], R R R unde [ f ] R := a 11 a 12 a 1n a 21 a 22 a 2n a n1 a n2 a nn, a ij = a ji, 1 i, jl Cornel Pintea Page 41 of 89 Babeş-Bolyai University 2016
45 Dacă R = (O, e 1,, e n) este un alt reper cartezian, atunci [M] R = T[M] R + [O ] R, ude T este matricea de trecere de la baza b = (e 1,, e n ) la baza b = (e 1,, e n), fapt care arată că f (M) = b (b 10 b n0 )[M] R + [M] t R (Tt [ f ] R T)[M] R, unde b 00 = a (a 10,, a n0 )[O ] R + [O ] t R [ f ] R [O ] R = f (O ) (b 10 b n0 ) = (a 10 a n0 )T [O ] t R ([ f ] R + [ f ]t R )T Aşadar [ f ] R = T t [ f ] R T O altă matrice importantă legată de reprezentarea funcţiei polinomiale f faţă de reperul R este a 00 a 01 a 02 a 0n a 10 a 11 a 12 a 1n [[ f ]] R := a 20 a 21 a 22 a 2n unde a 0i = a i0, i = 1, n a n0 a n1 a n2 a nn Într-adevăr avem f (M) = (1 x 1 x 2 x n )[[ f ]] R Dacă [M] t = (x R 1 x 2 x n), atunci avem 1 x 1 x 2 = unde unde Prin urmare avem x n β 1 t 11 t 12 t 1n β 2 t 21 t 22 t 2n β n t n1 t n2 t nn [O ] R = β 1 β 2 β n 1 x 1 x 2 x n şi T = (t ) ij 1 i,j n f (M) = (1 x 1 x 2 x n)(s t [[ f ]] R S) β 1 t 11 t 12 t 1n S = β 2 t 21 t 22 t 2n, β n t n1 t n2 t nn 1 x 1 x 2 x n 1 x 1 x 2 x n,, Cornel Pintea Page 42 of 89 Babeş-Bolyai University 2016
46 fapt care arată că [[ f ]] R = S t [[ f ]] R S 8 Săptămâna 8: Reducerea izometrică a polinoamelor de gradul doi în două variabile 81 Invarianţi ortogonali Fie π P un plan afin şi f : π R o funcţie polinomială de gradul doi reprezentată în raport cu reperul cartezian ortonormat R = (O, i, j ) de polinomul F = a a 10 X + 2a 20 Y + a 11 X 2 + 2a 12 XY + a 22 Y 2, adică ( ) a a11 a 00 a 01 a 02 [ f ] R = 12 şi [[ f ]] a 21 a R = a 10 a 11 a 12, a ij = a ji 22 a 20 a 21 a 22 Definiţia 81 O funcţie Φ : R 6 X se numeşte invariant ortogonal al funcţiei polinomiale f : π R, f (M) = a a 10 x + 2a 20 y + a 11 x 2 + 2a 12 xy + a 22 y 2 dacă valoarea Φ(a 00, a 10, a 20, a 11, a 12, a 22 ) nu se schimbă atunci când schimbăm reperul cartezian ortonormat Propoziţia 81 Polinomul caracteristic P(λ) = det([ f ] R λi 2 ) = a 11 λ a 12 a 21 a 22 λ = λ 2 I λ + δ, (a 21 = a 12 ) este invariant ortogonal al lui f În particular δ = det [ f ] R = a 11 a 12 a 21 a 22 = a11 a 22 a 2 12 şi I = Tr [ f ] R = a 11 + a 22 sunt invarianţi ortogonali ai lui f De asemenea determinantul a 00 a 01 a 02 = det [[ f ]] R = a 10 a 11 a 12 a 20 a 21 a 22, (a ik = a ki ) este invariant ortogonal al lui f numit discriminantul lui f Cornel Pintea Page 43 of 89 Babeş-Bolyai University 2016
47 82 Semiinvarianţi ortogonali Definiţia 82 semiinvariant ortogonal al funcţiei polinomiale f : π R, f (M) = a a 10 x + 2a 20 y + a 11 x 2 + 2a 12 xy + a 22 y 2 dacă valoarea Ψ(a 00, a 10, a 20, a 11, a 12, a 22 ) nu se schimbă atunci când schimbăm reperul cartezian ortonormat fără a schimba originea sa a 00 a 01 a 02 Propoziţia 82 Polinomul P O (λ) = a 10 a 11 λ a 12 a 20 a 21 a 22 λ = Kλ + a 00λ 2 este un semiinvariant ortogonal al lui f Prin urmare, K = a 00 a 01 a 10 a 11 + a 00 a 02 a 20 a 22 este un semiinvariant ortogonal al lui f Cornel Pintea Page 44 of 89 Babeş-Bolyai University 2016
48 83 Probleme 1 Să se calculeze invarianţii şi semiinvarianţii ortogonali ai polinoamelor de gradul 2: (a) αx 2 + 2βxy (α 2)y 2 + 2x + 2y + 2 = 0; (b) (α 1)x 2 + 2βxy (α + 1)y 2 + 2αx + 2βy (α + 1) = 0, α, β fiind coordonatele unui punct din plan Cornel Pintea Page 45 of 89 Babeş-Bolyai University 2016
49 2 Să se calculeze invarianţii şi semiinvarianţii ortogonali ai polinoamelor de gradul 2: (a) x 8y + 9x 2 4xy + 6y 2 ; (b) x + 12y + 4xy + 3y 2 ; (c) 1 6x + 2y + x 2 4xy + 4y 2 9 Săptămâna 9: Teorema de reducere izometrică a polinoamelor de gradul doi în două variabile Teorema 91 Faţă de un reper cartezian ortonormat convenabil ales funcţia polinomială f are una din formele următoare: 1 λ 1 x 2 + λ 2 y 2 + δ, dacă δ = 0; 2 Iy 2 ± 2 I x, dacă δ = 0, = 0; 3 Iy 2 + K I, dacă δ = = 0 În procesul de reducere al funcţiilor polinomiale de gradul doi, matricea simetrică [ f ] R se diagonalizează cu ajutorul unei baze de vectori proprii ai acestei matrici Direcţiile vectorilor unei astfel de baze, adică spaţiile generate de ei, se numesc direcţii principale ale funcţiei polinomiale în discuţie Cornel Pintea Page 46 of 89 Babeş-Bolyai University 2016
50 Teorema 92 (Teorema de reducere izometrică a conicelor) Dată fiind conica Q : a a 10 x + 2a 20 y + a 11 x 2 + 2a 12 xy + a 22 y 2 = 0 există un reper cartezian ortonormat convenabil ales astfel încât ecuaţia acesteia să aibă una din formele următoare: 1 λ 1 x 2 + λ 2 y 2 + δ = 0, dacă δ = 0; 2 Iy 2 ± 2 I x = 0, dacă δ = 0, = 0; 3 Iy 2 + K I = 0, dacă δ = = 0 = 0 δ > 0 I > 0 elipsă imaginară I < 0 elipsă reală conice δ < 0 hiperbolă nedegenerate δ = 0 parabolă = 0 δ > 0 două drepte secante imaginare δ < 0 două drepte secante reale conice δ = 0 K > 0 două drepte paralele imaginare degenerate K < 0 două drepte paralele reale K = 0 două drepte reale confundate Demonstraţia teoremei de reducere a polinoamelor de gradul doi in două variabile sugerează o metodă de a aduce conicele la forma canonică, numită metoda valorilor şi a vectorilor proprii În continuare vom prezenta o metodă alternativă de a găsi reperul R = (O, i, j ), faţă de care ecuaţia unei conice cu centru unic (ex elipsă, hiperbolă) are forma are forma redusă Cornel Pintea Page 47 of 89 Babeş-Bolyai University 2016
51 Originea O este centrul conicei Aşadar, coordonatele sale date de unica soluţie a sistemului { 12 F x(x, { y) = F y(x, y) = 0 a10 + a 11 x + a 12 y = 0 a 20 + a 12 x + a 22 y = 0 (91) Dacă θ = ( i, i ), atunci coordonatele lui i în raport cu baza iniţială [ i, j ] sunt (cos θ, sin θ) iar coordonatele lui j sunt ( sin θ, cos θ) Vectorii i, j fiind direcţiile principale corespunzătoare valorilor proprii λ 1 respectiv λ 2, coordonatele lor sunt soluţiile sistemelor { (a11 λ 1 ) cos θ + a 12 sin θ = 0 (92) a 12 cos θ + (a 22 λ 1 ) sin θ = 0 Prin urmare { (a11 λ 2 ) sin θ + a 12 cos θ = 0 a 12 sin θ + (a 22 λ 2 ) cos θ = 0 (93) λ 1 = a 11 + a 12 tgθ, λ 2 = a 11 a 12 ctgθ (94) Adunând relaţiile (94) şi ţinând seama de relaţia a 11 + a 22 = λ 1 + λ 2, deducem relaţia a 12 tg 2 θ + (a 11 a 22 )tgθ a 12 = 0 (95) Schimbând eventual rolul lui λ 1 cu cel al lui λ 2, baza [ i, j ] poate fi astfel alesă încât unghiul rotaţiei să fie între 0 şi π 2 Acest fapt împreună cu relaţia 95 determină în mod unic θ (cu excepţia cazului a 12 = 0, a 11 = a 22, când conica este un cerc şi θ poate lua orice valoare) care este unghiul rotaţiei axelor de coordonte Ecuaţia 95 este echivalentă cu ecuaţia (a 11 a 22 )tgθ = a 12 (1 tg 2 θ) sau cu ecuaţia Pantele direcţiilor asimptotice sunt date de ecuaţia tg2θ = 2a 12 a 11 a 22 (96) a 22 m 2 + 2a 12 m + a 11 = 0 (97) Notând cu m 1, m 2 cele două rădăcini ale ecuaţiei 97, ecuaţiile asimptotelor sunt: ecuaţia globală a celor două asimptote este F x + m i F y = 0, i {1, 2} (98) F(x, y) = δ (99) Cornel Pintea Page 48 of 89 Babeş-Bolyai University 2016
52 91 Probleme 1 Să se discute natura conicei ( Q α,β ) αx 2 + 2βxy (α 2)y 2 + 2x + 2y + 2 = 0, α, β fiind coordonatele unui punct din plan 2 Să se discute natura conicei ( ) Q α,β (α 1)x 2 + 2βxy (α + 1)y 2 + 2αx + 2βy (α + 1) = 0, α, β fiind coordonatele unui punct din plan Cornel Pintea Page 49 of 89 Babeş-Bolyai University 2016
53 3 Să se scrie ecuaţia redusă a conicei 9x 2 25y 2 18x + 50y 241 = 0 4 Să se aducă la forma redusă izometrică şi să se reprezinte grafic conicele: Cornel Pintea Page 50 of 89 Babeş-Bolyai University 2016
54 (a) Q 1 : x 8y + 9x 2 4xy + 6y 2 = 0 Cornel Pintea Page 51 of 89 Babeş-Bolyai University 2016
55 (b) Q 2 : x + 12y + 4xy + 3y 2 = 0 Cornel Pintea Page 52 of 89 Babeş-Bolyai University 2016
56 (c) Q 3 : 1 6x + 2y + x 2 4xy + 4y 2 = 0 Cornel Pintea Page 53 of 89 Babeş-Bolyai University 2016
57 10 Săptămâna 10: Reducerea izometrică a polinoamelor de gradul doi în trei variabile 101 Invarianţi şi semiinvarianţi ortogonali Fie g : P R o funcţie polinomială de gradul doi reprezentată faţă de reperul cartezian ortonormat R = (O, i, j, k ) prin unde g(m) = a 00 +2a 10 x + 2a 20 y + 2a 30 z +2a 12 xy + 2a 13 xz + 2a 23 yz +a 11 x 2 + a 22 y 2 + a 33 z 2 = a 00 +2(a 10 a 20 a 30 )[M] R + [M] t [g] [M], R R R [g] R = a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 Dacă R = (O, i, j, k ) este un alt reper cartezian ortonormat, amintim că [g]r = T t [g] R T, unde T este matricea ortonormată de trecere de la baza [ i, j, k ] la baza [ i, j, k ] Aşadar, rangul matricii [g] R nu depinde de alegerea reperului cartezian ortonormat R şi se notează cu r De altfel nici rangul matricii a 00 a 01 a 02 a 03 [[g]] R = a 10 a 11 a 12 a 13 a 20 a 21 a 22 a 23 a 30 a 31 a 32 a 33 nu depinde de alegerea reperului cartezian ortonormat R şi se notează cu r, deoarece [[g]] R = ( ) S t 1 0 [[g]] R S, unde S are forma Este uşor de verificat că r T {r, r + 1, r + 2} Amintim că pe lângă invarianţii numerici r şi r asociaţi funcţiei polinomiale g : P R, g(m) = a 00 +2a 10 x + 2a 20 y + 2a 30 z +2a 12 xy + 2a 13 xz + 2a 23 yz +a 11 x 2 + a 22 y 2 + a 33 z 2 = a 00 +2(a 10 a 20 a 30 )[M] R + [M] t R [g] R [M] R,, un alt invariant numeric al său asociat lui g este indicele pozitiv de inerţie i al formei pătratice 2a 12 xy + 2a 13 xz + 2a 23 yz + a 11 x 2 + a 22 y 2 + a 33 z 2, adică numărul valorilor proprii > 0 ale matricii [g] R Definiţia 101 O aplicaţie Φ : R 10 X se numeşte invariant ortogonal al funcţiei polinomiale dacă valoarea g : P R, g(m) = a 00 +2a 10 x + 2a 20 y + 2a 30 z +2a 12 xy + 2a 13 xz + 2a 23 yz +a 11 x 2 + 2a 22 y 2 + a 33 z 2 Φ(a 00, a 10, a 20, a 30, a 12, a 13, a 23, a 11, a 22, a 33 ) (101) nu se schimbă atunci când schimbăm reperul cartezian ortonormat Aplicaţia Φ se numeşte semiinvariant ortogonal al funcţiei polinomiale g dacă valoarea (101) nu se schimbă atunci când schimbăm reperul cartezian ortonormat, fără a schimba originea sa Cornel Pintea Page 54 of 89 Babeş-Bolyai University 2016
58 1011 Invarianţi ortogonali Propoziţia 101 Polinomul caracteristic a 11 λ a 12 a 13 P(λ) = a 21 a 22 λ a 23 a 31 a 32 a 33 λ = I 0 I 1 λ + I 2 λ 2 λ 3, unde a ji = a ij, este invariant ortogonal al lui g, adică a 11 a 12 a 13 I 0 = δ = a 21 a 22 a 23 a 31 a 32 a 33 I 1 = a 11 a 12 a 21 a 22 + a 11 a 13 a 31 a 33 I 2 = a 11 + a 22 + a 33 + a 22 a 23 a 32 a 33 sunt invarianţi ortogonali ai lui g De asemenea determinantul a 00 a 01 a 02 a 03 = det[[g]] R = a 10 a 11 a 12 a 13 a 20 a 21 a 22 a 23, (a ik = a ki ) a 30 a 31 a 32 a 33 este invariant ortogonal al lui g numit discriminantul lui g 1012 Semiinvarianţi ortogonali Propoziţia 102 Polinomul P O (λ) = a 00 a 01 a 02 a 03 a 10 a 11 λ a 12 a 13 a 20 a 21 a 22 λ a 23 a 30 a 31 a 32 a 33 λ (102) = K 1 λ + K 2 λ 2 λ 3 este un semiinvariant ortogonal al lui g, adică a 00 a 01 a 02 K 1 = a 10 a 11 a 12 a 20 a 21 a 22 + a 00 a 01 a 03 a 10 a 11 a 13 a 30 a 31 a 33 + K 2 = a 00 a 01 a 10 a 11 + a 00 a 02 a 20 a 22 + a 00 a 03 a 30 a 33 a 00 a 02 a 03 a 20 a 22 a 23 a 30 a 32 a 33 (103) sunt semiinvarianţi ortogonali ai funcţiei polinomiale g Observaţia 101 Dacă funcţia polinomială g : P R nu conţine variabila z când spaţiul P este raportat la reperul cartezian ortonormat R = (O, i, j, k ), atunci = 0 iar K 1 este un invariant ortogonal De asemenea dacă g nu conţine variabilele y, z, atunci = K 1 = 0 iar K 2 este un invariant ortogonal Cornel Pintea Page 55 of 89 Babeş-Bolyai University 2016
59 Într-adevăr, dacă g(m) = a a 10 x + 2a 20 y + a 11 x 2 + 2a 12 xy + a 22 y 2, atunci a 00 a 01 a 02 K 1 = δ = a 10 a 11 a 12 a 20 a 21 a 22 este invariant ortogonal al conicei Fie R = (O, i { g(m) = 0 z = 0 (104), j, k ) un alt reper cartezian ortonormat, unde O (α, β, γ) Valoarea lui K 1 nu se schimbă prin trecerea de la reperul R la reperul R 1 = (O 1, i, j, k ), unde O 1 (α, β, 0), deoarece K 1 este un invariant ortogonal al conicei { g(m) = 0 z = 0 De asemenea valoarea lui K 1 nu se schimbă prin trecerea de la reperul R 1 la reperul R 2 = (O, i, j, k ) deoarece forma funcţiei polinomiale g nu se schimbă prin această trecere În sfârşit, valoarea lui K 1 nu se schimbă prin trecerea de la reperul R 2 la reperul R deoarece K 1 este un semiinvariant ortogonal al funcţiei g Analog se arată că semiinvariantul K 2 este un invariant ortogonal dacă funcţia polinomială g nu conţine variabilele y, z 102 Teorema de reducere izometrică a polinoamelor de gradul doi în trei variabile Teorema 103 Faţă de un reper cartezian ortonormat convenabil ales funcţia polinomială g are una din formele următoare: 1 λ 1 x 2 + λ 2 y 2 + λ 3 z 2 + δ, dacă δ = 0; 2 λ 1 x 2 + λ 2 y 2 ± I 1 z dacă δ = 0, I 1 = 0, = 0; 3 λ 1 x 2 + λ 2 y 2 + K 1 I 1 dacă δ = 0, I 1 = 0, = 0; 4 I 2 x K 1 I 2 y dacă δ = 0, I 1 = 0, K 1 = 0; 5 I 2 x 2 + K 2 I 2 dacă δ = 0, I 1 = 0, K 1 = 0 Matricea T din demonstraţia teoremei 103 fiind ortogonală det T { 1, 1} De obicei vectorii i, j, k sunt astfel aleşi încât det T = 1, adică bazele [ i, j, k ] şi [ i, j, k ] să fie la fel orientate Dată fiind o funcţie polinomială de gradul doi g : P R, un invariant ortogonal al lui g se numeşte şi invariant ortogonal al cuadricei g 1 (0) Observăm de asemenea un semiinvariant ortogonal al lui g se numeşte şi semiinvariant ortogonal al cuadricei g 1 (0) Teorema 104 (Teorema de clasificare a cuadricelor) Dată fiind cuadrica Q : a 00 +2a 10 x + 2a 20 y + 2a 30 z +2a 12 xy + 2a 13 xz + 2a 23 yz +a 11 x 2 + 2a 22 y 2 + a 33 z 2 = 0 există un reper cartezian ortonormat convenabil ales astfel încât ecuaţia acesteia să aibă una din formele următoare: Cornel Pintea Page 56 of 89 Babeş-Bolyai University 2016
60 1 λ 1 x 2 + λ 2 y 2 + λ 3 z 2 + δ = 0, dacă δ = 0; 2 λ 1 x 2 + λ 2 y 2 ± I 1 z = 0 dacă δ = 0, I 1 = 0, = 0; 3 λ 1 x 2 + λ 2 y 2 + K 1 I 1 = 0 dacă δ = 0, I 1 = 0, = 0; 4 I 2 x K 1 I 2 y = 0 dacă δ = 0, I 1 = 0, K 1 = 0; 5 I 2 x 2 + K 2 I 2 = 0 dacă δ = 0, I 1 = 0, K 1 = 0 r r i (Semi)invarianţi Denumirea cuadricei ecuaţia canonică > 0 elipsoid imaginar < 0 elipsoid real λ 1 x 2 + λ 2 y 2 + λ 3 z 2 + δ = 0 2 > 0 hiperboloid cu o pânză < 0 hiperboloid cu două pânze 2 2 paraboloid eliptic λ 1 x 2 + λ 2 y 2 ± I 1 z = 0 1 parabolid hiperbolic punct dublu λ 1 x 2 + λ 2 y 2 + λ 3 z 2 = 0 2 con 2 2 K 1 I 1 > 0 cilindru eliptic imaginar K 1 I 1 < 0 cilindru eliptic real λ 1 x 2 + λ 2 y 2 + K 1 I 1 = 0 1 cilindru hiperbolic 1 1 cilindru parabolic I 2 x K 1 I 2 y = dreaptă dublă λ 1 x 2 + λ 2 y 2 = 0 1 pereche de plane secante 1 1 K 2 > 0 pereche vidă de plane K 2 < 0 pereche de plane paralele I 2 x 2 + K 2 I 2 = plan dublu x 2 = Probleme Să se studieze natura cuadricelor, să se aducă la forma redusă şi să se reprezinte în spaţiul tridimensional cuadricele: 1 Q 1 : x + 8y + 20z + 4yz + 36x 2 + 8y 2 + 5z 2 = 0; 2 Q 2 : x 2 + 3y 2 + 4yz 6x + 8y + 8 = 0; 3 Q 3 : 2y 2 + 4xy 8xz 4yz + 6x 5 = 0; 4 Q 4 : x 2 + y 2 z 2 4xy 4xz 6x = 0 Soluţie Vom trata aici doar punctele (2) şi (3), celelalte tratându-se analog (2) Notăm cu f funcţia polinomială de gradul doi care defineşte cuadrica Q 2 şi cu R reperul cartezian iniţial Dacă M este un punct din spaţiu de coordonate (x, y, z) faţă de R, atunci f (M) = x 2 + 3y 2 + 4yz 6x + 8y + 8 şi deci [ f ] R = şi [[ f ]] R = Cornel Pintea Page 57 of 89 Babeş-Bolyai University 2016
61 de unde rezultă că δ = = 4 şi = = = Valorile proprii ale matricii [ f ] R sunt rădăcinile polinomului său caracteristic, adică 1 λ λ 2 = 0 λ(1 λ)(3 λ) 4(1 λ) = λ (1 λ)( 3λ + λ 2 4) = 0 (λ 1)(λ + 1)(λ 4) = 0 Prin urmare ecuaţia canonică a cuadricei Q 2 este x 2 y 2 + 4z 2 = 1 x 2 y 2 + z 2 = 4 ( ) 1 2 = 1 (105) 2 şi ea reprezintă un hiperboloid cu o pânză 9 Subspaţiul propriu asociat valorii proprii λ 1 = 1 este soluţia generală a sistemului u 0 { v = 0 2v + 2w = 0 v = w = 0 2v w = w 0 Aşadar, un vector propriu asociat valorii proprii λ 1 = 1 este e 1 = i(1, 0, 0) Subspaţiul propriu asociat valorii proprii λ 1 = 1 este soluţia generală a sistemului u 0 2u = v = 0 4v + 2w = 0 u = 0 & w = 2v w 0 2v + w = 0 Aşadar, un vector propriu asociat valorii proprii λ 2 = 1 este e 2 = 1 5 j 2 5 k Subspaţiul propriu asociat valorii proprii λ 1 = 4 este soluţia generală a sistemului u 0 3u = v = 0 v + 2w = 0 u = 0 & v = 2w w 0 2v 4w = 0 Aşadar, un vector propriu asociat valorii proprii λ 2 = 4 este e 3 = 2 5 j k Matricea ortogonală a primei schimbări de coordonate este x = x 1 2 T = y = 0 2 iar schimbarea de coordonate este y z z = 2 5 y z 9 Aici se încheie studiul naturii cuadricei Q 2 Consideraţiile ulterioare au în vedere reprezentarea sa Cornel Pintea Page 58 of 89 Babeş-Bolyai University 2016
62 Faţă de reperul R = (O, e 1, e 2, e 3 ) funcţia f are forma f (M) = 8 + [ 6 8 0] 0 5 x y + x 2 y 2 + 4z 2 1 z 5 5 = 8 6x + 8 y + 16 z + +x 2 y 2 + 4z 2 5 ( 5 = x 2 6x y 2 8 y = (x 3) 2 ( y 4 5 ) 2 + ( z ) 2 1 A doua schimbare de coordonate este x = x 3 y = y 4 5 z = z + 2, 5 ) ( z z ) iar originea reperului faţă de care funcţia are forma redusă are coordonatele x = 3 x = 3 x = 0 y y = 0 = y = ( 2 ) x = z = 0, z = 2 z = ( 2 ) y = 0 z = , adică originea O a reperului faţă de care funcţia f are forma redusă are, faţă de reperul iniţial R, coordonatele (3, 0, 2) Faţă de reperul R = (O e 1, e 2, e 3 ) cuadrica Q 2 are ecuaţia (105) Amintim faptul că originea O a reperului R coincide cu centrul hiperboloidului cu o pânză Q 2 şi deci coordonatele sale se pot găsi şi rezolvând sistemul liniar f x = 0 f y = 0 f z = 0 Cornel Pintea Page 59 of 89 Babeş-Bolyai University 2016
63 (3) Notăm cu f funcţia polinomială de gradul doi care defineşte cuadrica Q 3 şi cu R reperul cartezian iniţial Dacă M este un punct din spaţiu de coordonate (x, y, z) faţă de R, atunci f (M) = 2y 2 + 4xy 8xz 4yz + 6x 5 şi deci [ f ] R = şi [[ f ]] R = de unde rezultă că δ = = = 0, = = = 5( ) 3 3 ( 4) = 36, I 1 = = = 24 Valorile proprii ale matricii [ f ] R sunt rădăcinile polinomului său caracteristic, adică λ λ λ = 0 λ2 (2 λ) (2 λ) + 4λ + 4λ = 0 λ 2 (2 λ) λ + 8λ = 0 λ(λ 2 2λ 24 = 0 λ 1 = 6, λ 2 = 4, λ 3 = 0 Prin urmare ecuaţia canonică a cuadricei Q 3 este 6x 2 4y 2 ± z = 0 6x 2 4y 2 ± 6z = 0 şi ea reprezintă un paraboloid hiperbolic 10 Subspaţiul propriu asociat valorii proprii λ 1 = 6 este soluţia generală a sistemului u 0 6u + 2v 4w = 0 { v = 0 u = 2v + w +2u 4v 2w = 0 u = v = w v = w w 0 4u 2v 6w = 0 Aşadar, un vector propriu asociat valorii proprii λ 1 = 6 este e 1 = 1 3 i j 1 3 k Subspaţiul propriu asociat valorii proprii λ 2 = 4 este soluţia generală a sistemului u 0 4u + 2v 4w = v = 0 2u + 6v 2w = w 0 4u 2v + 4w = 0 { v = 2u + 2w u 6u + 6w w = 0 { u = w v = 0 10 Aici se încheie studiul naturii cuadricei Q 3 Consideraţiile ulterioare au în vedere reprezentarea sa Cornel Pintea Page 60 of 89 Babeş-Bolyai University 2016
64 Aşadar, un vector propriu asociat valorii proprii λ 2 = 4 este e 2 = 1 2 i k Subspaţiul propriu asociat valorii proprii λ 3 = 4 este soluţia generală a sistemului u 0 2v 4w = v = 0 2u + 2v 2w = 0 v = 2u = 2w w 0 4u 2v = 0 Aşadar, un vector propriu asociat valorii proprii λ 3 = 0 este e 3 = 1 6 i 2 6 j 1 6 k Matricea ortogonală a primei schimbări de coordonate este T = iar schimbarea de coordonate este: x = y = 1 3 x y z 1 3 x 2 6 z z = 1 3 x y 1 6 z Faţă de reperul R = (O, e 1, e 2, e 3 ) funcţia f are forma f (M) = 8 + [6 0 0] ( x y z x 3 + y 2 + z 6 ) + 6x 2 4y 2 = ( = 6 x x ( = 6 x ) 2 4 ( y ) 12 4 ( y x 2 4y y + 9 ) z 5 ) ) ( z A doua schimbare de coordonate este x = x y = y z = z , Cornel Pintea Page 61 of 89 Babeş-Bolyai University 2016
65 iar originea reperului faţă de care funcţia are forma redusă are coordonatele x = 1 x = 0 2 x = y = 0 y = z = 0, 4 y = z = z = x = 3 4 y = z = 3 8, adică originea O a reperului ( faţă de ) care funcţia f are forma redusă are, faţă de reperul 3 iniţial R, coordonatele 4, 39 24, 3 Faţă de acest reper paraboloidul hiperbolic Q 3 are 8 ecuaţia 6x 2 4y 2 + 6z = 0 11 Săptămâna 11 Morfisme liniare şi aplicaţii afine Definiţia 111 Fie (X, X, ϕ), (Y, Y, ψ) două spaţii afine şi f : X Y 1 Aplicaţia f se numeşte morfism liniar dacă f transformă varietăţile liniare ale lui X în varietăţi liniare ale lui Y, adică L A(X) = f (L) A(Y) 2 f se numeşte aplicaţie afină sau morfism afin dacă există o aplicaţie liniară f : X Y, numită urma sau aplicaţia liniară tangentă, astfel încât f (M) f (N)= f ( MN) pentru orice puncte M, N X Cornel Pintea Page 62 of 89 Babeş-Bolyai University 2016
Geometrie afină Conf. Univ. Dr. Cornel Pintea cpintea math.ubbcluj.ro Cuprins 1 Săptămâna Endomorfismele unui spaţiu afin Transla
 Geometrie afină Conf Univ Dr Cornel Pintea E-mail: cpintea mathubbclujro Cuprins 1 Săptămâna 12 1 2 Endomorfismele unui spaţiu afin 1 21 Translaţia 1 22 Subspaţii invariante 2 23 Omotetii 2 3 Apendix 2
Geometrie afină Conf Univ Dr Cornel Pintea E-mail: cpintea mathubbclujro Cuprins 1 Săptămâna 12 1 2 Endomorfismele unui spaţiu afin 1 21 Translaţia 1 22 Subspaţii invariante 2 23 Omotetii 2 3 Apendix 2
Microsoft Word - cap1p4.doc
 Algebră liniară, geometrie analitică şi diferenţială.6 Subspaţii vectoriale Fie V un spaţiu vectorial peste corpul K. În cele ce urmează vom introduce două definiţii echivalente pentru noţiunea de subspaţiu
Algebră liniară, geometrie analitică şi diferenţială.6 Subspaţii vectoriale Fie V un spaţiu vectorial peste corpul K. În cele ce urmează vom introduce două definiţii echivalente pentru noţiunea de subspaţiu
Cursul 12 (plan de curs) Integrale prime 1 Sisteme diferenţiale autonome. Spaţiul fazelor. Fie Ω R n o mulţime deschisă şi f : Ω R n R n o funcţie de
 Cursul 12 (plan de curs) Integrale prime 1 Sisteme diferenţiale autonome. Spaţiul fazelor. Fie Ω R n o mulţime deschisă şi f : Ω R n R n o funcţie de clasă C 1. Vom considera sistemul diferenţial x = f(x),
Cursul 12 (plan de curs) Integrale prime 1 Sisteme diferenţiale autonome. Spaţiul fazelor. Fie Ω R n o mulţime deschisă şi f : Ω R n R n o funcţie de clasă C 1. Vom considera sistemul diferenţial x = f(x),
Facultatea de Matematică Anul II Master, Geometrie Algebrică Mulţimi algebrice ireductibile. Dimensiune 1 Mulţimi ireductibile Propoziţia 1.1. Fie X u
 Facultatea de Matematică Anul II Master, Geometrie Algebrică Mulţimi algebrice ireductibile. Dimensiune 1 Mulţimi ireductibile Propoziţia 1.1. Fie X un spaţiu topologic. Următoarele afirma-ţii sunt echivalente:
Facultatea de Matematică Anul II Master, Geometrie Algebrică Mulţimi algebrice ireductibile. Dimensiune 1 Mulţimi ireductibile Propoziţia 1.1. Fie X un spaţiu topologic. Următoarele afirma-ţii sunt echivalente:
PROGRAMA CONCURSULUI NAŢIONAL
 ANUL ŞCOLAR 2011-2012 CLASA a IX-a În programa de concurs pentru clasa a IX-a sunt incluse conţinuturile programelor din clasele anterioare şi din etapele anterioare. 1. Mulţimi şi elemente de logică matematică.
ANUL ŞCOLAR 2011-2012 CLASA a IX-a În programa de concurs pentru clasa a IX-a sunt incluse conţinuturile programelor din clasele anterioare şi din etapele anterioare. 1. Mulţimi şi elemente de logică matematică.
Gheorghe IUREA Adrian ZANOSCHI algebră geometrie clasa a VII-a ediţia a V-a, revizuită mate 2000 standard EDITURA PARALELA 45 Matematică. Clasa a VII-
 Gheorghe IUREA Adrian ZANOSCHI algebră geometrie clasa a VII-a ediţia a V-a, revizuită mate 2000 standard 3 Algebră Capitolul I. MULŢIMEA NUMERELOR RAŢIONALE Identificarea caracteristicilor numerelor raţionale
Gheorghe IUREA Adrian ZANOSCHI algebră geometrie clasa a VII-a ediţia a V-a, revizuită mate 2000 standard 3 Algebră Capitolul I. MULŢIMEA NUMERELOR RAŢIONALE Identificarea caracteristicilor numerelor raţionale
I
 METODA VECTORIALĂ ÎN GEOMETRIE prof. Andrei - Octavian Dobre Această metodă poate fi descrisă după cum urmează: Fiind dată o problemă de geometrie, după explicitarea şi reprezentarea grafică a configuraţiei
METODA VECTORIALĂ ÎN GEOMETRIE prof. Andrei - Octavian Dobre Această metodă poate fi descrisă după cum urmează: Fiind dată o problemă de geometrie, după explicitarea şi reprezentarea grafică a configuraţiei
Microsoft Word - D_ MT1_II_001.doc
 ,1 SUBIECTUL II (30p) Varianta 1001 a b 1 Se consideră matricea A = b a, cu a, b şi 0 http://wwwpro-matematicaro a) Să se arate că dacă matricea X M ( ) verifică relaţia AX = XA, atunci există uv,, astfel
,1 SUBIECTUL II (30p) Varianta 1001 a b 1 Se consideră matricea A = b a, cu a, b şi 0 http://wwwpro-matematicaro a) Să se arate că dacă matricea X M ( ) verifică relaţia AX = XA, atunci există uv,, astfel
Cursul 8 Funcţii analitice Vom studia acum comportarea şirurilor şi seriilor de funcţii olomorfe, cu scopul de a dezvălui o proprietate esenţială a ac
 Cursul 8 Funcţii analitice Vom studia acum comportarea şirurilor şi seriilor de funcţii olomorfe, cu scopul de a dezvălui o proprietate esenţială a acestor funcţii: analiticitatea. Ştim deja că, spre deosebire
Cursul 8 Funcţii analitice Vom studia acum comportarea şirurilor şi seriilor de funcţii olomorfe, cu scopul de a dezvălui o proprietate esenţială a acestor funcţii: analiticitatea. Ştim deja că, spre deosebire
Pachete de lecţii disponibile pentru platforma AeL
 Pachete de lecţii disponibile pentru platforma AeL -disciplina Matematică- Nr. crt Nume pachet clasa Nr. momente Nr.Recomandat de ore 1 Corpuri geometrice V 6 1 2 Fracţii V 14 5 3 Măsurarea lungimilor.
Pachete de lecţii disponibile pentru platforma AeL -disciplina Matematică- Nr. crt Nume pachet clasa Nr. momente Nr.Recomandat de ore 1 Corpuri geometrice V 6 1 2 Fracţii V 14 5 3 Măsurarea lungimilor.
Distanţa euclidiană (indusă de norma euclidiană) (în R k ). Introducem în continuare o altă aplicaţie, de această dată pe produsul cartezian R k XR k,
 Distanţa euclidiană (indusă de norma euclidiană) (în R k ). Introducem în continuare o altă aplicaţie, de această dată pe produsul cartezian R k XR k, aplicaţie despre care vom vedea că reprezintă generalizarea
Distanţa euclidiană (indusă de norma euclidiană) (în R k ). Introducem în continuare o altă aplicaţie, de această dată pe produsul cartezian R k XR k, aplicaţie despre care vom vedea că reprezintă generalizarea
Examenul de bacalaureat 2012
 CENTRUL NAŢIONAL DE EVALUARE ŞI EXAMINARE PROGRAMA DE EXAMEN PENTRU DISCIPLINA MATEMATICĂ BACALAUREAT 2015 PROGRAMA M_tehnologic Filiera tehnologică, profilul servicii, toate calificările profesionale,
CENTRUL NAŢIONAL DE EVALUARE ŞI EXAMINARE PROGRAMA DE EXAMEN PENTRU DISCIPLINA MATEMATICĂ BACALAUREAT 2015 PROGRAMA M_tehnologic Filiera tehnologică, profilul servicii, toate calificările profesionale,
Tiberiu Trif Analiză matematică 2 Calcul diferențial și integral în R n
 Tiberiu Trif Analiză matematică 2 Calcul diferențial și integral în R n Cuprins Notații v 1 Topologie în R n 1 1.1 Spațiul euclidian R n........................ 1 1.2 Structura topologică a spațiului
Tiberiu Trif Analiză matematică 2 Calcul diferențial și integral în R n Cuprins Notații v 1 Topologie în R n 1 1.1 Spațiul euclidian R n........................ 1 1.2 Structura topologică a spațiului
D.Rusu, Teoria măsurii şi integrala Lebesgue 6 MĂSURA LEBESGUE Cursul 5 Teorema 6.26 Există submulţimi ale lui R care nu sunt măsurabile Lebesgue. Dem
 D.Rusu, Teoria măsurii şi integrala Lebesgue 6 MĂSURA LEBESGUE Cursul 5 Teorema 6.26 Există submulţimi ale lui R care nu sunt măsurabile Lebesgue. Demonstraţie. Fie mulţimea A = [0, ], pe care definim
D.Rusu, Teoria măsurii şi integrala Lebesgue 6 MĂSURA LEBESGUE Cursul 5 Teorema 6.26 Există submulţimi ale lui R care nu sunt măsurabile Lebesgue. Demonstraţie. Fie mulţimea A = [0, ], pe care definim
Prelegerea 4 În această prelegere vom învăţa despre: Algebre booleene; Funcţii booleene; Mintermi şi cuburi n - dimensionale. 4.1 Definirea algebrelor
 Prelegerea 4 În această prelegere vom învăţa despre: Algebre booleene; Funcţii booleene; Mintermi şi cuburi n - dimensionale. 4.1 Definirea algebrelor booleene Definiţia 4.1 Se numeşte algebră Boole (booleană)
Prelegerea 4 În această prelegere vom învăţa despre: Algebre booleene; Funcţii booleene; Mintermi şi cuburi n - dimensionale. 4.1 Definirea algebrelor booleene Definiţia 4.1 Se numeşte algebră Boole (booleană)
CURBE BÉZIER În CAGD se utilizează adesea curbele polinomiale, adică acele curbe definite de o parametrizare polinomială: C : [a, b] R 3 C(t) = (x(t),
![CURBE BÉZIER În CAGD se utilizează adesea curbele polinomiale, adică acele curbe definite de o parametrizare polinomială: C : [a, b] R 3 C(t) = (x(t), CURBE BÉZIER În CAGD se utilizează adesea curbele polinomiale, adică acele curbe definite de o parametrizare polinomială: C : [a, b] R 3 C(t) = (x(t),](/thumbs/101/150500936.jpg) CURE ÉZIER În CAGD se utilizează adesea curbele polinomiale, adică acele curbe definite de o parametrizare polinomială: C : [a, b] R 3 C(t) = (x(t), y(t), z(t)) cu x, y, z polinoame de grad n. Maximul
CURE ÉZIER În CAGD se utilizează adesea curbele polinomiale, adică acele curbe definite de o parametrizare polinomială: C : [a, b] R 3 C(t) = (x(t), y(t), z(t)) cu x, y, z polinoame de grad n. Maximul
Examenul de bacalaureat 2012
 PROGRAMA PENTRU SIMULAREA EXAMENULUI DE BACALAUREAT 2019 LA DISCIPLINA MATEMATICĂ În cadrul examenului de Bacalaureat 2019, Programele de examen la disciplina Matematica se diferenţiază în funcţie de filiera,
PROGRAMA PENTRU SIMULAREA EXAMENULUI DE BACALAUREAT 2019 LA DISCIPLINA MATEMATICĂ În cadrul examenului de Bacalaureat 2019, Programele de examen la disciplina Matematica se diferenţiază în funcţie de filiera,
Examenul de bacalaureat 2012
 INSPECTORATUL Ș C O L A R J U D E Ț E A N C O V A S N A PROGRAMA PENTRU SIMULAREA EXAMENULUI DE BACALAUREAT 2015 LA DISCIPLINA MATEMATICĂ În cadrul examenului de Bacalaureat 2015, Programele de examen
INSPECTORATUL Ș C O L A R J U D E Ț E A N C O V A S N A PROGRAMA PENTRU SIMULAREA EXAMENULUI DE BACALAUREAT 2015 LA DISCIPLINA MATEMATICĂ În cadrul examenului de Bacalaureat 2015, Programele de examen
Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică Gheorghe Asachi Iaşi, 2015 Analiză Matematică Lucian Maticiuc 1 / 29
 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică Gheorghe Asachi Iaşi, 2015 Analiză Matematică Lucian Maticiuc 1 / 29 Definiţie. Şiruri mărginite. Şiruri monotone. Subşiruri ale
Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică Gheorghe Asachi Iaşi, 2015 Analiză Matematică Lucian Maticiuc 1 / 29 Definiţie. Şiruri mărginite. Şiruri monotone. Subşiruri ale
Lucian L. TURDEANU Georgeta D. POP (MANEA) BAZELE GEOMETRICE ALE FOTOGRAMETRIEI CONSPRESS BUCUREŞTI 2009
 Lucian L. TURDEANU Georgeta D. POP (MANEA) BAZELE GEOMETRICE ALE FOTOGRAMETRIEI CONSPRESS BUCUREŞTI 2009 CUPRINS Pg. INTRODUCERE. Noţiuni preliminare (L. Turdeanu, G. Pop)... 6 Probleme... 11 1. GEOMETRIA
Lucian L. TURDEANU Georgeta D. POP (MANEA) BAZELE GEOMETRICE ALE FOTOGRAMETRIEI CONSPRESS BUCUREŞTI 2009 CUPRINS Pg. INTRODUCERE. Noţiuni preliminare (L. Turdeanu, G. Pop)... 6 Probleme... 11 1. GEOMETRIA
Algebra si Geometri pentru Computer Science
 Natura este scrisă în limbaj matematic. Galileo Galilei 5 Aplicatii liniare Grafica vectoriala In grafica pe calculator, grafica vectoriala este un procedeu prin care imaginile sunt construite cu ajutorul
Natura este scrisă în limbaj matematic. Galileo Galilei 5 Aplicatii liniare Grafica vectoriala In grafica pe calculator, grafica vectoriala este un procedeu prin care imaginile sunt construite cu ajutorul
Cursul 6 Cadru topologic pentru R n În continuarea precedentei părţi, din cursul 5, dedicată, în întregime, unor aspecte de ordin algebric (relative l
 Cursul 6 Cadru topologic pentru R n În continuarea precedentei părţi, din cursul 5, dedicată, în întregime, unor aspecte de ordin algebric (relative la R n, în principal), sunt prezentate aici elemente
Cursul 6 Cadru topologic pentru R n În continuarea precedentei părţi, din cursul 5, dedicată, în întregime, unor aspecte de ordin algebric (relative la R n, în principal), sunt prezentate aici elemente
DAN LASCU ADRIANA-LIGIA SPORIŞ ANDA OLTEANU PAUL VASILIU MATEMATICĂ. CULEGERE DE PROBLEME TIP GRILĂ PENTRU ADMITEREA ÎN ACADEMIA NAVALĂ MIRCEA CEL BĂT
 DAN LASCU ADRIANA-LIGIA SPORIŞ ANDA OLTEANU PAUL VASILIU MATEMATICĂ. CULEGERE DE PROBLEME TIP GRILĂ PENTRU ADMITEREA ÎN ACADEMIA NAVALĂ MIRCEA CEL BĂTRÂN Colecţia Matematică DAN LASCU ADRIANA-LIGIA SPORIŞ
DAN LASCU ADRIANA-LIGIA SPORIŞ ANDA OLTEANU PAUL VASILIU MATEMATICĂ. CULEGERE DE PROBLEME TIP GRILĂ PENTRU ADMITEREA ÎN ACADEMIA NAVALĂ MIRCEA CEL BĂTRÂN Colecţia Matematică DAN LASCU ADRIANA-LIGIA SPORIŞ
Universitatea Politehnica din Bucureşti 2019 Disciplina: Geometrie şi Trigonometrie G1 * Varianta A 1. Ştiind cos x = 3 2, atunci sin2 x
 1 5 6 7 Universitatea Politehnica din Bucureşti 019 Disciplina: Geometrie şi Trigonometrie G1 * Varianta A 1 Ştiind cos x atunci sin x este: (6 pct a 1 ; b 1 ; c 1 ; d ; e 1 8 ; f Soluţie Folosind prima
1 5 6 7 Universitatea Politehnica din Bucureşti 019 Disciplina: Geometrie şi Trigonometrie G1 * Varianta A 1 Ştiind cos x atunci sin x este: (6 pct a 1 ; b 1 ; c 1 ; d ; e 1 8 ; f Soluţie Folosind prima
CONCURSUL NAŢIONAL DE MATEMATICA PANAITOPOL EDIŢIA a X-a, TULCEA, 21 aprilie 2018 Clasa a VII - a 1. Se consideră numerele reale x, y şi z, cel puţin
 CONCURSUL NAŢIONAL DE MATEMATICA PANAITOPOL EDIŢIA a X-a, TULCEA, 21 aprilie 2018 Clasa a VII - a 1. Se consideră numerele reale x, y şi z, cel puţin două dintre ele fiind diferite. Arătaţi că x y z 0
CONCURSUL NAŢIONAL DE MATEMATICA PANAITOPOL EDIŢIA a X-a, TULCEA, 21 aprilie 2018 Clasa a VII - a 1. Se consideră numerele reale x, y şi z, cel puţin două dintre ele fiind diferite. Arătaţi că x y z 0
Spatii vectoriale
 Algebra si Geometrie Seminar 2 Octombrie 2017 ii Matematica poate fi definită ca materia în care nu ştim niciodată despre ce vorbim, nici dacă ceea ce spunem este adevărat. Bertrand Russell 1 Spatii vectoriale
Algebra si Geometrie Seminar 2 Octombrie 2017 ii Matematica poate fi definită ca materia în care nu ştim niciodată despre ce vorbim, nici dacă ceea ce spunem este adevărat. Bertrand Russell 1 Spatii vectoriale
UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ Concurs MATE-INFO UBB 6 aprilie 2019 Proba scrisă la MATEMATICĂ NOTĂ IM
 UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ Concurs MATE-INFO UBB 6 aprilie 219 Proba scrisă la MATEMATICĂ NOTĂ IMPORTANTĂ: 1) Problemele de tip grilă din Partea A pot
UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ Concurs MATE-INFO UBB 6 aprilie 219 Proba scrisă la MATEMATICĂ NOTĂ IMPORTANTĂ: 1) Problemele de tip grilă din Partea A pot
BAC 2007 Pro Didactica Programa M1 2 Rezolvarea variantei 36 versiune finală Redactia Pro Didactica Suportul pe net:
 BAC 27 Pro Didactica Programa M1 2 Rezolvarea variantei 36 versiune finală Redactia Pro Didactica Suportul pe net: http://www./ CAPITOLUL 1 Varianta 36 1. Subiectul I. (a) Avem 2 ( ) 2+ ( ) 2= 7i = 2 7
BAC 27 Pro Didactica Programa M1 2 Rezolvarea variantei 36 versiune finală Redactia Pro Didactica Suportul pe net: http://www./ CAPITOLUL 1 Varianta 36 1. Subiectul I. (a) Avem 2 ( ) 2+ ( ) 2= 7i = 2 7
Analiz¼a Matematic¼a - Curs 6 M¼ad¼alina Roxana Buneci
 Analiz¼a Matematic¼a - Curs 6 M¼ad¼alina Roxana Buneci Cuprins 4 Spaţii topologice (continuare din cursul 5) 3 4.6 Spaţiul R n............................ 3 5 Calcul diferenţial 7 5. Derivatele funcţiilor
Analiz¼a Matematic¼a - Curs 6 M¼ad¼alina Roxana Buneci Cuprins 4 Spaţii topologice (continuare din cursul 5) 3 4.6 Spaţiul R n............................ 3 5 Calcul diferenţial 7 5. Derivatele funcţiilor
Teoreme cu nume 1. Problema (Năstăsescu IX, p 147, propoziţia 5) Formula lui Chasles Pentru orice puncte M, N şi P avem MN + NP = MP.
 Teoreme cu nume Problema (Năstăsescu IX, p 47, propoziţia 5) Formula lui hasles Pentru orice puncte M, N şi P avem MN + NP = MP 2 Problema (Năstăsescu IX, p 68, teoremă) Vectorul de poziţie al centrului
Teoreme cu nume Problema (Năstăsescu IX, p 47, propoziţia 5) Formula lui hasles Pentru orice puncte M, N şi P avem MN + NP = MP 2 Problema (Năstăsescu IX, p 68, teoremă) Vectorul de poziţie al centrului
Coordonate baricentrice Considerăm în plan un triunghi ABC şi un punct Q în interiorul său, fixat arbitrar. Notăm σ c = aria ( QAB) σ a = aria ( QBC),
 Coordonate baricentrice Considerăm în plan un triunghi ABC şi un punct Q în interiorul său, fixat arbitrar Notăm σ c = aria ( QAB) = aria ( QBC), = aria ( QCA) şi σ = aria ( ABC), astfel încât σ = + +
Coordonate baricentrice Considerăm în plan un triunghi ABC şi un punct Q în interiorul său, fixat arbitrar Notăm σ c = aria ( QAB) = aria ( QBC), = aria ( QCA) şi σ = aria ( ABC), astfel încât σ = + +
Prelegerea 3 În această prelegere vom învăţa despre: Clase speciale de latici: complementate. modulare, metrice, distributive şi 3.1 Semi-distributivi
 Prelegerea 3 În această prelegere vom învăţa despre: Clase speciale de latici: complementate. modulare, metrice, distributive şi 3.1 Semi-distributivitate şi semi - modularitate Fie L o latice. Se numeşte
Prelegerea 3 În această prelegere vom învăţa despre: Clase speciale de latici: complementate. modulare, metrice, distributive şi 3.1 Semi-distributivitate şi semi - modularitate Fie L o latice. Se numeşte
TEORIA MĂSURII Liviu C. Florescu Universitatea Al.I.Cuza, Facultatea de Matematică, Bd. Carol I, 11, R Iaşi, ROMANIA, e mail:
 TEORI MĂSURII Liviu C. Florescu Universitatea l.i.cuza, Facultatea de Matematică, Bd. Carol I, 11, R 700506 Iaşi, ROMNI, e mail: lflo@uaic.ro În mod intenţionat această pagină este lăsată albă! Cuprins
TEORI MĂSURII Liviu C. Florescu Universitatea l.i.cuza, Facultatea de Matematică, Bd. Carol I, 11, R 700506 Iaşi, ROMNI, e mail: lflo@uaic.ro În mod intenţionat această pagină este lăsată albă! Cuprins
RecMat dvi
 Conice şi cubice în probleme elementare de loc geometric Ştefan DOMINTE 1 Abstract. In this Note, a number of simple problems are presented to support the idea that conic and cubic curves can frequently
Conice şi cubice în probleme elementare de loc geometric Ştefan DOMINTE 1 Abstract. In this Note, a number of simple problems are presented to support the idea that conic and cubic curves can frequently
Dorel LUCHIAN Gabriel POPA Adrian ZANOSCHI Gheorghe IUREA algebră geometrie clasa a VIII-a ediţia a V-a, revizuită mate 2000 standard EDITURA PARALELA
 Dorel LUCHIAN Gabriel POPA Adrian ZANOSCHI Gheorghe IUREA algebră geometrie clasa a VIII-a ediţia a V-a, revizuită mate 000 standard 3 10 PP Algebră Capitolul I. NUMERE REALE Competenţe specifice: Determinarea
Dorel LUCHIAN Gabriel POPA Adrian ZANOSCHI Gheorghe IUREA algebră geometrie clasa a VIII-a ediţia a V-a, revizuită mate 000 standard 3 10 PP Algebră Capitolul I. NUMERE REALE Competenţe specifice: Determinarea
BAC 2007 Pro Didactica Programa M1 2 Rezolvarea variantei 61 versiune finală Redactia Pro Didactica Suportul pe net:
 BAC 7 Pro Didactica Programa M Rezolvarea variantei 6 versiune finală Redactia Pro Didactica Suportul pe net: http://www./ CAPITOLUL Varianta 6. Subiectul I. (a) Coordonatele punctelor C şi D satisfac
BAC 7 Pro Didactica Programa M Rezolvarea variantei 6 versiune finală Redactia Pro Didactica Suportul pe net: http://www./ CAPITOLUL Varianta 6. Subiectul I. (a) Coordonatele punctelor C şi D satisfac
Clasa IX 1. O lăcustă face salturi, fiecare salt în linie dreaptă şi de două ori mai lung ca precedentul. Poate vreodată lăcusta să revină în punctul
 Clasa IX. O lăcustă face salturi, fiecare salt în linie dreaptă şi de două ori mai lung ca precedentul. Poate vreodată lăcusta să revină în punctul de plecare iniţial? Soluţie. Răspunsul este negativ.
Clasa IX. O lăcustă face salturi, fiecare salt în linie dreaptă şi de două ori mai lung ca precedentul. Poate vreodată lăcusta să revină în punctul de plecare iniţial? Soluţie. Răspunsul este negativ.
FIŞA DISCIPLINEI
 FIŞA DISCIPLINEI 1. Date despre program 1.1.Instituţia de învăţământ superior Universitatea SPIRU HARET 1.2.Facultatea Inginerie, Informatică şi Geografie 1.3.Departamentul Informatică şi Geografie 1.4.Domeniul
FIŞA DISCIPLINEI 1. Date despre program 1.1.Instituţia de învăţământ superior Universitatea SPIRU HARET 1.2.Facultatea Inginerie, Informatică şi Geografie 1.3.Departamentul Informatică şi Geografie 1.4.Domeniul
Microsoft Word - Programa finala olimpiadei matematica 2007 gimnaziu.doc
 ROMÂNIA MINISTERUL EDUCAŢIEI ŞI CERCETĂRII DIRECŢIA GENERALĂ ÎNVĂŢĂMÂNT PREUNIVERSITAR SERVICIUL NAŢIONAL DE EVALUARE ŞI EXAMINARE PROGRAMA OLIMPIADEI DE MATEMATICĂ CLASELE V XII AN ŞCOLAR 006 / 007 Pentru
ROMÂNIA MINISTERUL EDUCAŢIEI ŞI CERCETĂRII DIRECŢIA GENERALĂ ÎNVĂŢĂMÂNT PREUNIVERSITAR SERVICIUL NAŢIONAL DE EVALUARE ŞI EXAMINARE PROGRAMA OLIMPIADEI DE MATEMATICĂ CLASELE V XII AN ŞCOLAR 006 / 007 Pentru
MD.09. Teoria stabilităţii 1
 MD.09. Teoria stabilităţii 1 Capitolul MD.09. Teoria stabilităţii Cuvinte cheie Soluţie stabilă spre +, instabilă si asimptotic stabilă, punct de echilibru, soluţie staţionară, stabilitatea soluţiei banale,
MD.09. Teoria stabilităţii 1 Capitolul MD.09. Teoria stabilităţii Cuvinte cheie Soluţie stabilă spre +, instabilă si asimptotic stabilă, punct de echilibru, soluţie staţionară, stabilitatea soluţiei banale,
gaussx.dvi
 Algebră liniarăi 1 Recapitulare cunoştiinţe de algebră din clasa XI-a În clasa a XI s-a studiat la algebră problema existenţei soluţiei 1 şi calculării soluţiei sistemelor liniare 2 (adică sisteme care
Algebră liniarăi 1 Recapitulare cunoştiinţe de algebră din clasa XI-a În clasa a XI s-a studiat la algebră problema existenţei soluţiei 1 şi calculării soluţiei sistemelor liniare 2 (adică sisteme care
Cursul 7 Formula integrală a lui Cauchy Am demonstrat în cursul precedent că, dacă D C un domeniu simplu conex şi f : D C o funcţie olomorfă cu f cont
 Cursul 7 Formula integrală a lui Cauchy Am demonstrat în cursul precedent că, dacă D C un domeniu simplu conex şi f : D C o funcţie olomorfă cu f continuă pe D, atunci, pe orice curbă rectificabilă şi
Cursul 7 Formula integrală a lui Cauchy Am demonstrat în cursul precedent că, dacă D C un domeniu simplu conex şi f : D C o funcţie olomorfă cu f continuă pe D, atunci, pe orice curbă rectificabilă şi
programa_olimpiada_matematica_IX-XII_
 R O M  N I A MINISTERUL EDUCAłIEI, CERCETĂRII ŞI TINERETULUI DIRECłIA GENERALĂ MANAGEMENT ÎNVĂłĂMÂNT PREUNIVERSITAR CONSILIUL NAłIONAL PENTRU CURRICULUM ŞI EVALUARE ÎN ÎNVĂłĂMÂNTUL PREUNIVERITAR PROGRAMA
R O M  N I A MINISTERUL EDUCAłIEI, CERCETĂRII ŞI TINERETULUI DIRECłIA GENERALĂ MANAGEMENT ÎNVĂłĂMÂNT PREUNIVERSITAR CONSILIUL NAłIONAL PENTRU CURRICULUM ŞI EVALUARE ÎN ÎNVĂłĂMÂNTUL PREUNIVERITAR PROGRAMA
CLP_UTCN-grila-2012.dvi
 Liceul: Numele: Punctaj: Prenumele: Concursul liceelor partenere cu Universitatea Tehnică din Cluj-Napoca Test grilă Ediţia a treia mai 0 Clasa a X-a În casuţa din stânga întrebării se va scrie litera
Liceul: Numele: Punctaj: Prenumele: Concursul liceelor partenere cu Universitatea Tehnică din Cluj-Napoca Test grilă Ediţia a treia mai 0 Clasa a X-a În casuţa din stânga întrebării se va scrie litera
Aproximarea functiilor prin metoda celor mai mici patrate
 Aproximarea funcţiilor prin metoda celor mai mici pătrate Prof.dr.ing. Universitatea "Politehnica" Bucureşti, Facultatea de Inginerie Electrică Suport didactic pentru disciplina Metode numerice, 2017-2018
Aproximarea funcţiilor prin metoda celor mai mici pătrate Prof.dr.ing. Universitatea "Politehnica" Bucureşti, Facultatea de Inginerie Electrică Suport didactic pentru disciplina Metode numerice, 2017-2018
Ecuatii si sisteme de ecuatii neliniare 1 Metoda lui Newton Algorithm 1 Metoda lui Newton pentru ecuaţia f(x) = 0. Date de intrare: - Funcţia f - Apro
 Ecuatii si sisteme de ecuatii neliniare Metoda lui Newton Algorithm Metoda lui Newton pentru ecuaţia f(x) = 0. - Funcţia f - Aproximaţia iniţială x - Eroarea admisă ε - Numărul maxim de iteraţii ITMAX
Ecuatii si sisteme de ecuatii neliniare Metoda lui Newton Algorithm Metoda lui Newton pentru ecuaţia f(x) = 0. - Funcţia f - Aproximaţia iniţială x - Eroarea admisă ε - Numărul maxim de iteraţii ITMAX
C:/Users/Lenovo/Dropbox/activitate matematica/cursuri/MS ETTI /msetti.dvi
 Curs 1 Noţiuni de teoria câmpului 1.1 Vectori şi operaţii cu vectori 1.1.1 Scalari şi vectori Definiţie 1.1. Un număr real λ R se va numi scalar. O pereche de numere reale (a 1,a ) R se va numi vector
Curs 1 Noţiuni de teoria câmpului 1.1 Vectori şi operaţii cu vectori 1.1.1 Scalari şi vectori Definiţie 1.1. Un număr real λ R se va numi scalar. O pereche de numere reale (a 1,a ) R se va numi vector
Noțiuni matematice de bază
 Sistem cartezian definitie. Coordonate carteziene Sistem cartezian definiţie Un sistem cartezian de coordonate (coordonatele carteziene) reprezintă un sistem de coordonate plane ce permit determinarea
Sistem cartezian definitie. Coordonate carteziene Sistem cartezian definiţie Un sistem cartezian de coordonate (coordonatele carteziene) reprezintă un sistem de coordonate plane ce permit determinarea
GHEORGHE PROCOPIUC PROBLEME DE ANALIZĂ MATEMATICĂ ŞI ECUAŢII DIFERENŢIALE IAŞI, 2007
 GHEORGHE PROCOPIUC PROBLEME DE ANALIZĂ MATEMATICĂ ŞI ECUAŢII DIFERENŢIALE IAŞI, 7 Cuprins Elemente de teoria spaţiilor metrice 4 Spaţii metrice 4 Mulţimea numerelor reale 8 Şiruri şi serii 5 Şiruri de
GHEORGHE PROCOPIUC PROBLEME DE ANALIZĂ MATEMATICĂ ŞI ECUAŢII DIFERENŢIALE IAŞI, 7 Cuprins Elemente de teoria spaţiilor metrice 4 Spaţii metrice 4 Mulţimea numerelor reale 8 Şiruri şi serii 5 Şiruri de
Elemente de aritmetica
 Elemente de aritmetică Anul II Februarie 2017 Divizibilitate în Z Definiţie Fie a, b Z. Spunem că a divide b (scriem a b) dacă există c Z astfel încât b = ac. In acest caz spunem că a este un divizor al
Elemente de aritmetică Anul II Februarie 2017 Divizibilitate în Z Definiţie Fie a, b Z. Spunem că a divide b (scriem a b) dacă există c Z astfel încât b = ac. In acest caz spunem că a este un divizor al
8
 9.5 Fluxul unui vector printr-o suprafaţă deschisă-continuare Observaţie: Dacă vrem să calculăm fluxul vectorului a = P x y z i + Q x y z j + R x y z k (,, ) (,, ) (,, ) prin suprafaţa definită de ecuaţia
9.5 Fluxul unui vector printr-o suprafaţă deschisă-continuare Observaţie: Dacă vrem să calculăm fluxul vectorului a = P x y z i + Q x y z j + R x y z k (,, ) (,, ) (,, ) prin suprafaţa definită de ecuaţia
Examenul de bacalaureat 2012
 2 MONITORUL OFICIAL AL ROMÂNIEI, PARTEA I, Nr. 696/7.IX.2016 ACTE ALE ORGANELOR DE SPECIALITATE ALE ADMINISTRAȚIEI PUBLICE CENTRALE MINISTERUL EDUCAȚIEI NAȚIONALE ȘI CERCETĂRII ȘTIINȚIFICE ORDIN privind
2 MONITORUL OFICIAL AL ROMÂNIEI, PARTEA I, Nr. 696/7.IX.2016 ACTE ALE ORGANELOR DE SPECIALITATE ALE ADMINISTRAȚIEI PUBLICE CENTRALE MINISTERUL EDUCAȚIEI NAȚIONALE ȘI CERCETĂRII ȘTIINȚIFICE ORDIN privind
Teoria Grafurilor şi Combinatorică recapitulare Principii de numărare Reţineţi că: P (n, r) este numărul de şiruri (sau r-permutări) de forma A 1,...,
 Teoria Grafurilor şi Combinatorică recapitulare Principii de numărare Reţineţi că: P (n, r) este numărul de şiruri (sau r-permutări) de forma A,..., A r unde A,..., A r sunt elemente distincte dintr-o
Teoria Grafurilor şi Combinatorică recapitulare Principii de numărare Reţineţi că: P (n, r) este numărul de şiruri (sau r-permutări) de forma A,..., A r unde A,..., A r sunt elemente distincte dintr-o
Aero-BCD, , Prof. L. Costache & M. Olteanu Notițe de Adrian Manea Seminar 5 Șiruri și serii de funcții. Serii de puteri 1 Șiruri de funcții D
 Seminar 5 Șiruri și serii de funcții. Serii de puteri Șiruri de funcții Definiţie.: Fie (f n ) n un șir de funcții, cu fiecare f n : [a, b] R și fie o funcție f : [a, b] R. PC Spunem că șirul (f n ) converge
Seminar 5 Șiruri și serii de funcții. Serii de puteri Șiruri de funcții Definiţie.: Fie (f n ) n un șir de funcții, cu fiecare f n : [a, b] R și fie o funcție f : [a, b] R. PC Spunem că șirul (f n ) converge
Curs 10 Aplicaţii ale calculului diferenţial. Puncte de extrem 10.1 Diferenţiale de ordin superior S¼a trecem acum la de nirea diferenţialelor de ordi
 Curs 0 Aplicaţii ale calculului diferenţial. Puncte de extrem 0. Diferenţiale de ordin superior S¼a trecem acum la de nirea diferenţialelor de ordin superior. De niţia 0.. Fie n 2; D R k o mulţime deschis¼a
Curs 0 Aplicaţii ale calculului diferenţial. Puncte de extrem 0. Diferenţiale de ordin superior S¼a trecem acum la de nirea diferenţialelor de ordin superior. De niţia 0.. Fie n 2; D R k o mulţime deschis¼a
Retele Petri si Aplicatii
 Reţele Petri şi Aplicaţii Curs 3 RPA (2019) Curs 3 1 / 48 Conţinutul cursului 1 Arbori de acoperire 2 Probleme de decizie în reţele Petri 3 Invarianţi tranziţie RPA (2019) Curs 3 2 / 48 Arbori de acoperire
Reţele Petri şi Aplicaţii Curs 3 RPA (2019) Curs 3 1 / 48 Conţinutul cursului 1 Arbori de acoperire 2 Probleme de decizie în reţele Petri 3 Invarianţi tranziţie RPA (2019) Curs 3 2 / 48 Arbori de acoperire
Probleme date la examenul de logică matematică şi computaţională. Partea a II-a Claudia MUREŞAN Universitatea din Bucureşti Facultatea de Matematică ş
 Probleme date la examenul de logică matematică şi computaţională. Partea a II-a Claudia MUREŞAN Universitatea din Bucureşti Facultatea de Matematică şi Informatică Academiei 4, RO 0004, Bucureşti, România
Probleme date la examenul de logică matematică şi computaţională. Partea a II-a Claudia MUREŞAN Universitatea din Bucureşti Facultatea de Matematică şi Informatică Academiei 4, RO 0004, Bucureşti, România
Logică și structuri discrete Relații. Funcții parțiale Marius Minea marius/curs/lsd/ 20 octombrie 2014
 Logică și structuri discrete Relații. Funcții parțiale Marius Minea marius@cs.upt.ro http://www.cs.upt.ro/ marius/curs/lsd/ 20 octombrie 2014 Relații în lumea reală și informatică Noțiunea matematică de
Logică și structuri discrete Relații. Funcții parțiale Marius Minea marius@cs.upt.ro http://www.cs.upt.ro/ marius/curs/lsd/ 20 octombrie 2014 Relații în lumea reală și informatică Noțiunea matematică de
matematica
 MINISTERUL EDUCAŢIEI, CERCETĂRII ŞI INOVĂRII PROGRAMĂ ŞCOLARĂ M A T E M A T I C Ă CLASA A IX-A CICLUL INFERIOR AL LICEULUI Aprobată prin ordin al ministrului nr. / Bucureşti, 2009 NOTĂ DE PREZENTARE În
MINISTERUL EDUCAŢIEI, CERCETĂRII ŞI INOVĂRII PROGRAMĂ ŞCOLARĂ M A T E M A T I C Ă CLASA A IX-A CICLUL INFERIOR AL LICEULUI Aprobată prin ordin al ministrului nr. / Bucureşti, 2009 NOTĂ DE PREZENTARE În
Limbaje de ordinul I LOGICA DE ORDINUL I Un limbaj L de ordinul I este format din: o mulţime numărabilă V = {v n n N} de variabile; conectorii şi ; pa
 Limbaje de ordinul I LOGICA DE ORDINUL I Un limbaj L de ordinul I este format din: o mulţime numărabilă V = {v n n N} de variabile; conectorii şi ; paranteze: (, ); simbolul de egalitate =; cuantificatorul
Limbaje de ordinul I LOGICA DE ORDINUL I Un limbaj L de ordinul I este format din: o mulţime numărabilă V = {v n n N} de variabile; conectorii şi ; paranteze: (, ); simbolul de egalitate =; cuantificatorul
ETTI-AM2, , M. Joița & A. Niță Notițe de Adrian Manea Seminar 11 Transformarea Laplace Aplicații Transformarea Z Ecuații și sisteme diferenți
 Seminar Transformarea Laplace Aplicații Transformarea Z Ecuații și sisteme diferențiale Folosind transformata Laplace, putem reolva ecuații și sisteme diferențiale. Cu ajutorul proprietăților transformatei
Seminar Transformarea Laplace Aplicații Transformarea Z Ecuații și sisteme diferențiale Folosind transformata Laplace, putem reolva ecuații și sisteme diferențiale. Cu ajutorul proprietăților transformatei
Examenul de bacalaureat 2012
 2 MONITORUL OFICIAL AL ROMÂNIEI, PARTEA I, Nr. 696/7.IX.2016 ACTE ALE ORGANELOR DE SPECIALITATE ALE ADMINISTRAȚIEI PUBLICE CENTRALE MINISTERUL EDUCAȚIEI NAȚIONALE ȘI CERCETĂRII ȘTIINȚIFICE ORDIN privind
2 MONITORUL OFICIAL AL ROMÂNIEI, PARTEA I, Nr. 696/7.IX.2016 ACTE ALE ORGANELOR DE SPECIALITATE ALE ADMINISTRAȚIEI PUBLICE CENTRALE MINISTERUL EDUCAȚIEI NAȚIONALE ȘI CERCETĂRII ȘTIINȚIFICE ORDIN privind
FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituţia de învăţământ superior Universitatea Alexandru Ioan Cuza din Iaşi 1.2 Facultatea Facultatea de
 FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituţia de învăţământ superior Universitatea Alexandru Ioan Cuza din Iaşi 1.2 Facultatea Facultatea de Matematică 1.3 Departamentul Matematică Didactic 1.4
FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituţia de învăţământ superior Universitatea Alexandru Ioan Cuza din Iaşi 1.2 Facultatea Facultatea de Matematică 1.3 Departamentul Matematică Didactic 1.4
1. Găsiți k numerele cele mai apropiate într-un şir nesortat Dându-se un şir nesortat și două numere x și k, găsiți k cele mai apropiate valori de x.
 1. Găsiți k numerele cele mai apropiate într-un şir nesortat Dându-se un şir nesortat și două numere x și k, găsiți k cele mai apropiate valori de x. Date de intrare: arr [] = {10, 2, 14, 4, 7, 6}, x =
1. Găsiți k numerele cele mai apropiate într-un şir nesortat Dându-se un şir nesortat și două numere x și k, găsiți k cele mai apropiate valori de x. Date de intrare: arr [] = {10, 2, 14, 4, 7, 6}, x =
COMENTARII FAZA JUDEŢEANĂ, 9 MARTIE 2013 Abstract. Personal comments on some of the problems presented at the District Round of the National Mathemati
 COMENTARII FAZA JUDEŢEANĂ, 9 MARTIE 2013 Abstract. Personal comments on some of the problems presented at the District Round of the National Mathematics Olympiad 2013. Data: 12 martie 2013. Autor: Dan
COMENTARII FAZA JUDEŢEANĂ, 9 MARTIE 2013 Abstract. Personal comments on some of the problems presented at the District Round of the National Mathematics Olympiad 2013. Data: 12 martie 2013. Autor: Dan
CONCURSUL NAŢIONAL DE MATEMATICA PANAITOPOL EDIŢIA a X-a, TULCEA, 21 aprilie 2018 Clasa a VII - a Soluţii orientative şi bareme Problema 1. Se conside
 CONCURSUL NAŢIONAL DE MATEMATICA PANAITOPOL EDIŢIA a X-a, TULCEA, 1 aprilie 18 Clasa a VII - a Soluţii orientative şi bareme Problema 1. Se consideră numerele reale x, y şi z, cel puţin două dintre ele
CONCURSUL NAŢIONAL DE MATEMATICA PANAITOPOL EDIŢIA a X-a, TULCEA, 1 aprilie 18 Clasa a VII - a Soluţii orientative şi bareme Problema 1. Se consideră numerele reale x, y şi z, cel puţin două dintre ele
CONCURSUL DE MATEMATICĂ APLICATĂ "ADOLF HAIMOVICI" ETAPA JUDEȚEANĂ 18 martie 2017 Filiera Tehnologică : profilul Tehnic Clasa a IX -a Problema 1. 2 Se
 Clasa a IX -a Se consideră funcţia f : R R, f ( x) x mx 07, unde mr a) Determinaţi valoarea lui m ştiind că f( ), f() şi f () sunt termeni consecutivi ai unei progresii aritmetice b) Dacă f() f(4), să
Clasa a IX -a Se consideră funcţia f : R R, f ( x) x mx 07, unde mr a) Determinaţi valoarea lui m ştiind că f( ), f() şi f () sunt termeni consecutivi ai unei progresii aritmetice b) Dacă f() f(4), să
PAS cap. 2: Reprezentări rare p. 1/35 Prelucrarea avansată a semnalelor Capitolul 2: Reprezentări rare Bogdan Dumitrescu Facultatea de Automatică şi C
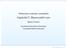 PAS cap. 2: Reprezentări rare p. 1/35 Prelucrarea avansată a semnalelor Capitolul 2: Reprezentări rare Bogdan Dumitrescu Facultatea de Automatică şi Calculatoare Universitatea Politehnica Bucureşti PAS
PAS cap. 2: Reprezentări rare p. 1/35 Prelucrarea avansată a semnalelor Capitolul 2: Reprezentări rare Bogdan Dumitrescu Facultatea de Automatică şi Calculatoare Universitatea Politehnica Bucureşti PAS
PowerPoint Presentation
 ELEMENTE DE MORFOLOGIE MATEMATICA Morfologia matematica Cadru de abordare diferit: Pana acum : Imaginea este o functie de doua variabile. Pixelii imaginii (valori si coordonate de pozitie) sunt structurati
ELEMENTE DE MORFOLOGIE MATEMATICA Morfologia matematica Cadru de abordare diferit: Pana acum : Imaginea este o functie de doua variabile. Pixelii imaginii (valori si coordonate de pozitie) sunt structurati
Laborator 4 Modele sistemice liniare. Reprezentare numerică. Conversii. Conexiuni 4.1 Tema Formarea deprinderilor de utilizare a convenţiilor MATLAB d
 Laborator 4 Modele sistemice liniare Reprezentare numerică Conversii Conexiuni 41 Tema Formarea deprinderilor de utilizare a convenţiilor MATLAB de reprezentare numerică a modelelor sitemice de stare şi
Laborator 4 Modele sistemice liniare Reprezentare numerică Conversii Conexiuni 41 Tema Formarea deprinderilor de utilizare a convenţiilor MATLAB de reprezentare numerică a modelelor sitemice de stare şi
Şcoala ………
 Şcoala... Clasa a X-a Disciplina: Matematică TC + CD Anul şcolar: 07-08 TC = trunchi comun 35 săptămâni: 8 săptămâni semestrul I CD = curriculum diferenţiat Nr. ore: 3 ore / săptămână 7 săptămâni semestrul
Şcoala... Clasa a X-a Disciplina: Matematică TC + CD Anul şcolar: 07-08 TC = trunchi comun 35 săptămâni: 8 săptămâni semestrul I CD = curriculum diferenţiat Nr. ore: 3 ore / săptămână 7 săptămâni semestrul
LOGICA MATEMATICA SI COMPUTATIONALA Sem. I,
 LOGICA MATEMATICĂ ŞI COMPUTAŢIONALĂ Sem. I, 2017-2018 Ioana Leustean FMI, UB Partea III Calculul propoziţional clasic Consistenţă şi satisfiabilitate Teorema de completitudine Algebra Lindenbaum-Tarski
LOGICA MATEMATICĂ ŞI COMPUTAŢIONALĂ Sem. I, 2017-2018 Ioana Leustean FMI, UB Partea III Calculul propoziţional clasic Consistenţă şi satisfiabilitate Teorema de completitudine Algebra Lindenbaum-Tarski
Logică și structuri discrete Mulțimi Casandra Holotescu
 Logică și structuri discrete Mulțimi Casandra Holotescu casandra@cs.upt.ro https://tinyurl.com/lectureslsd Mulțimi aspecte teoretice Ce sunt mulțimile? Mulțimea e un concept matematic fundamental. Definiție
Logică și structuri discrete Mulțimi Casandra Holotescu casandra@cs.upt.ro https://tinyurl.com/lectureslsd Mulțimi aspecte teoretice Ce sunt mulțimile? Mulțimea e un concept matematic fundamental. Definiție
20 SUBIECTE DE EXAMEN - De fapt, în pofida acestor probleme, până la urmă tot vom logaritma, căci aceasta este tehnica naturală în context. Trebuie do
 SUBIECTE DE EXAMEN - De fapt, în pofida acestor probleme, până la urmă tot vom logaritma, căci aceasta este tehnica naturală în context. Trebuie doar să gestionăm cu precauţie detaliile, aici fiind punctul
SUBIECTE DE EXAMEN - De fapt, în pofida acestor probleme, până la urmă tot vom logaritma, căci aceasta este tehnica naturală în context. Trebuie doar să gestionăm cu precauţie detaliile, aici fiind punctul
Notiuni de algebra booleana
 Noţiuni de algebră booleană (în lucru) Definiţie Algebră booleană = o structură algebrică formată din: O mulţime B Două operaţii binare notate cu (+) şi (.) O operaţie unară notată cu ( ) pentru care sunt
Noţiuni de algebră booleană (în lucru) Definiţie Algebră booleană = o structură algebrică formată din: O mulţime B Două operaţii binare notate cu (+) şi (.) O operaţie unară notată cu ( ) pentru care sunt
Microsoft Word - TIC5
 CAPACITATEA CANALELOR DE COMUNICAŢIE CAPITOLUL 5 CAPACITATEA CANALELOR DE COMUNICAŢIE În Capitolul 3, am văzut că putem utiliza codarea sursă pentru a reduce redundanţa inerentă a unei surse de informaţie
CAPACITATEA CANALELOR DE COMUNICAŢIE CAPITOLUL 5 CAPACITATEA CANALELOR DE COMUNICAŢIE În Capitolul 3, am văzut că putem utiliza codarea sursă pentru a reduce redundanţa inerentă a unei surse de informaţie
Microsoft Word - Programa_Evaluare_Nationala_2011_Matematica.doc
 C E N T R U L NAłIONAL DE EVALUARE ŞI E X A M I N A R E PROGRAMA PENTRU DISCIPLINA MATEMATICĂ EVALUAREA NAłIONALĂ PENTRU ELEVII CLASEI A VIII A Pagina 1 din 5 PROGRAMA PENTRU DISCIPLINA MATEMATICĂ I. STATUTUL
C E N T R U L NAłIONAL DE EVALUARE ŞI E X A M I N A R E PROGRAMA PENTRU DISCIPLINA MATEMATICĂ EVALUAREA NAłIONALĂ PENTRU ELEVII CLASEI A VIII A Pagina 1 din 5 PROGRAMA PENTRU DISCIPLINA MATEMATICĂ I. STATUTUL
Calcul Numeric
 Calcul Numeric Cursul 6 2019 Anca Ignat Algoritmul lui Givens Fie A o matrice reală pătratică de dimensiune n. Pp. că avem: A QR unde Q este o matrice ortogonală iar R este o matrice superior triunghiulară.
Calcul Numeric Cursul 6 2019 Anca Ignat Algoritmul lui Givens Fie A o matrice reală pătratică de dimensiune n. Pp. că avem: A QR unde Q este o matrice ortogonală iar R este o matrice superior triunghiulară.
ALGEBRA PENTRU INFORMATICĂ GEORGE CIPRIAN MODOI Cuprins Bibliografie 2 1. Mulţimi, Funcţii, Relaţii Preliminarii logice 3 Exerciţii la Prelimin
 ALGEBRA PENTRU INFORMATICĂ GEORGE CIPRIAN MODOI Cuprins Bibliografie 2 1. Mulţimi, Funcţii, Relaţii 3 1.1. Preliminarii logice 3 Exerciţii la Preliminarii logice 3 1.2. Mulţimi 3 Operaţii cu mulţimi 4
ALGEBRA PENTRU INFORMATICĂ GEORGE CIPRIAN MODOI Cuprins Bibliografie 2 1. Mulţimi, Funcţii, Relaţii 3 1.1. Preliminarii logice 3 Exerciţii la Preliminarii logice 3 1.2. Mulţimi 3 Operaţii cu mulţimi 4
Calcul Numeric
 Calcul Numeric Cursul 4 2019 Anca Ignat Metode numerice de rezolvarea sistemelor liniare Fie matricea nesingulară A nn şi b n. Rezolvarea sistemului de ecuații liniare Ax=b se poate face folosind regula
Calcul Numeric Cursul 4 2019 Anca Ignat Metode numerice de rezolvarea sistemelor liniare Fie matricea nesingulară A nn şi b n. Rezolvarea sistemului de ecuații liniare Ax=b se poate face folosind regula
Cursul 1 1. Introducere Corpul numerelor complexe Dezvoltarea istorică a gândirii matematice a urmărit îndeaproape evoluţia ideii de număr. Această ev
 Cursul 1 1. Introducere Corpul numerelor complexe Dezvoltarea istorică a gândirii matematice a urmărit îndeaproape evoluţia ideii de număr. Această evoluţie, exprimată succint prin şirul de incluziuni
Cursul 1 1. Introducere Corpul numerelor complexe Dezvoltarea istorică a gândirii matematice a urmărit îndeaproape evoluţia ideii de număr. Această evoluţie, exprimată succint prin şirul de incluziuni
2
 C5: Metoda matricilor de transfer BIBLIOGRAFIE E. Tulcan Paulescu, M. Paulescu Algorithms for electronic states in artificial semiconductors of use in intermediate band solar cells engineering. In Physics
C5: Metoda matricilor de transfer BIBLIOGRAFIE E. Tulcan Paulescu, M. Paulescu Algorithms for electronic states in artificial semiconductors of use in intermediate band solar cells engineering. In Physics
O teoremă de reprezentare (II) Marian TETIVA 1 Abstract. In this paper some (in general well-known) results on complete sequences are exposed, with ap
 O teoremă de reprezentare (II) Marian TETIVA 1 Abstract. In this paper some (in general well-known) results on complete sequences are exposed, with applications to Erdős-Suranyi sequences. We start from
O teoremă de reprezentare (II) Marian TETIVA 1 Abstract. In this paper some (in general well-known) results on complete sequences are exposed, with applications to Erdős-Suranyi sequences. We start from
matematica, liceu-specializ. matematica-informatica
 Anexa 2 la ordinul ministrului educaţiei şi cercetării nr. 3252/ 13.02.2006 MINISTERUL EDUCAŢIEI ŞI CERCETĂRII CONSILIUL NAŢIONAL PENTRU CURRICULUM PROGRAME ŞCOLARE PENTRU CICLUL SUPERIOR AL LICEULUI MATEMATICĂ
Anexa 2 la ordinul ministrului educaţiei şi cercetării nr. 3252/ 13.02.2006 MINISTERUL EDUCAŢIEI ŞI CERCETĂRII CONSILIUL NAŢIONAL PENTRU CURRICULUM PROGRAME ŞCOLARE PENTRU CICLUL SUPERIOR AL LICEULUI MATEMATICĂ
0 Probleme pentru pregătirea examenului final la Analiză Matematică 1. Să se calculeze următoarele integrale improprii: dx a) x 4 ; b) x 3 dx dx
 Probleme pentru pregătirea examenului final la Analiză Matematică. ă se calculeze următoarele integrale improprii: dx a) + x ; b) x dx dx; c) + x x + x ) ; dx x d) x + x ) ; e) dx; f) x p e xq dx, p >,
Probleme pentru pregătirea examenului final la Analiză Matematică. ă se calculeze următoarele integrale improprii: dx a) + x ; b) x dx dx; c) + x x + x ) ; dx x d) x + x ) ; e) dx; f) x p e xq dx, p >,
ALGORITMICĂ. Seminar 3: Analiza eficienţei algoritmilor - estimarea timpului de execuţie şi notaţii asimptotice. Problema 1 (L) Să se determine număru
 ALGORITMICĂ. Seminar 3: Analiza eficienţei algoritmilor - estimarea timpului de execuţie şi notaţii asimptotice. Problema 1 (L) Să se determine numărul de operaţii efectuate de către un algoritm care determină
ALGORITMICĂ. Seminar 3: Analiza eficienţei algoritmilor - estimarea timpului de execuţie şi notaţii asimptotice. Problema 1 (L) Să se determine numărul de operaţii efectuate de către un algoritm care determină
Calcul Numeric
 Calcul Numeric Cursul 7 2019 Aca Igat Memorarea matricelor rare - se memorează doar valorile eule şi suficiete iformaţii despre idici astfel ca să se poată recostitui complet matricea Pp. că matricea A
Calcul Numeric Cursul 7 2019 Aca Igat Memorarea matricelor rare - se memorează doar valorile eule şi suficiete iformaţii despre idici astfel ca să se poată recostitui complet matricea Pp. că matricea A
Matematica VI
 There are no translations available. Datorita unor probleme tehnice, site-ul nu poate fi vizionat cu Internet Explorer 8, partea de teste (apare pagina alba). Pentru navigare, va recomandam Chrome, Mozilla,
There are no translations available. Datorita unor probleme tehnice, site-ul nu poate fi vizionat cu Internet Explorer 8, partea de teste (apare pagina alba). Pentru navigare, va recomandam Chrome, Mozilla,
BARAJ NR. 1 JUNIORI FRANŢA ianuarie Fie x şi y două numere întregi astfel încât 5x + 6y şi 6x + 5y să fie pătrate perfecte. Arătaţi că
 BARAJ NR. 1 JUNIORI FRANŢA 019 9 ianuarie 019 1. Fie x şi y două numere întregi astfel încât 5x + 6y şi 6x + 5y să fie pătrate perfecte. Arătaţi că x şi y sunt divizibili cu 11.. Fie Γ un cerc de centru
BARAJ NR. 1 JUNIORI FRANŢA 019 9 ianuarie 019 1. Fie x şi y două numere întregi astfel încât 5x + 6y şi 6x + 5y să fie pătrate perfecte. Arătaţi că x şi y sunt divizibili cu 11.. Fie Γ un cerc de centru
Copyright c 2001 ONG TCV Scoala Virtuala a Tanarului Matematician 1 Ministerul Educatiei si Stiintei Examenul de bacalaureat la
 Copyright c 1 ONG TCV Scoala Virtuala a Tanarului Matematician http://math.ournet.md 1 Ministerul Educatiei si Stiintei Examenul de bacalaureat la matematica, Profilurile: fizica-matematica, economie,
Copyright c 1 ONG TCV Scoala Virtuala a Tanarului Matematician http://math.ournet.md 1 Ministerul Educatiei si Stiintei Examenul de bacalaureat la matematica, Profilurile: fizica-matematica, economie,
Curs 3 Permutari cu repetitie. Combinari. Algoritmi de ordonare si generare
 Curs 3 Permutări cu repetiţie. Combinări. Algoritmi de ordonare şi generare Octombrie 2015 Cuprins Algoritmi de ordonare şi generare pentru permutări cu repetiţie Reprezentarea binară a submulţimilor Algoritmi
Curs 3 Permutări cu repetiţie. Combinări. Algoritmi de ordonare şi generare Octombrie 2015 Cuprins Algoritmi de ordonare şi generare pentru permutări cu repetiţie Reprezentarea binară a submulţimilor Algoritmi
Microsoft Word - Matematika_kozep_irasbeli_jav_utmut0513V28_roman.doc
 Matematika román nyelven középszint 0513 ÉRETTSÉGI VIZSGA 005. május 8. MATEMATIKA ROMÁN NYELVEN MATEMATICĂ KÖZÉPSZINTŰ ÉRETTSÉGI VIZSGA EXAMEN DE BACALAUREAT NIVEL MEDIU Az írásbeli vizsga időtartama:
Matematika román nyelven középszint 0513 ÉRETTSÉGI VIZSGA 005. május 8. MATEMATIKA ROMÁN NYELVEN MATEMATICĂ KÖZÉPSZINTŰ ÉRETTSÉGI VIZSGA EXAMEN DE BACALAUREAT NIVEL MEDIU Az írásbeli vizsga időtartama:
Concursul de Matematică Upper.School ediția 2019 Etapa III - Clasa a 7-a Lista de probleme PROBLEMA 1 / 4 punctaj: 7 Aflați numerele prime p, q, r car
 Concursul de Matematică Upper.School ediția 2019 Etapa III - Clasa a 7-a Lista de probleme PROBLEMA 1 / 4 punctaj: 7 Aflați numerele prime p, q, r care satisfac simultan următoarele condiții: qr p 4 1
Concursul de Matematică Upper.School ediția 2019 Etapa III - Clasa a 7-a Lista de probleme PROBLEMA 1 / 4 punctaj: 7 Aflați numerele prime p, q, r care satisfac simultan următoarele condiții: qr p 4 1
C:/Users/Lenovo/Dropbox/activitate matematica/cursuri/MS IE /msie.dvi
 urs 2 Integrale de suprafaţă 2.1 Pânze şi suprafeţe Definiţie 2.1. Fie D R 2 o mulţime conexă şi deschisă. O funcţie continuă σ : D R 3 se numeşte pânză de suprafaţă. ulţimea = σd) se numeşte imaginea
urs 2 Integrale de suprafaţă 2.1 Pânze şi suprafeţe Definiţie 2.1. Fie D R 2 o mulţime conexă şi deschisă. O funcţie continuă σ : D R 3 se numeşte pânză de suprafaţă. ulţimea = σd) se numeşte imaginea
Subiectul 1
 Subiectul 1 În fişierul Numere.txt pe prima linie este memorat un număr natural n (n
Subiectul 1 În fişierul Numere.txt pe prima linie este memorat un număr natural n (n
Similitudini în plan şi puncte Torricelli asociate Cătălin ŢIGĂERU 1 Subiectul lucrării îl reprezintă operaţia de compunere a similitudinilor aplicată
 Similitudini în plan şi puncte Torricelli asociate Cătălin ŢIGĂERU 1 Subiectul lucrării îl reprezintă operaţia de compunere a similitudinilor aplicată unei configuraţii geometrice: un triunghi ABC şi două
Similitudini în plan şi puncte Torricelli asociate Cătălin ŢIGĂERU 1 Subiectul lucrării îl reprezintă operaţia de compunere a similitudinilor aplicată unei configuraţii geometrice: un triunghi ABC şi două
Microsoft PowerPoint - Curs_SDA_9_RO_2019_v2.pptx
 SDA (PC2) Curs 9 Liste / Grafuri / Arbori Iulian Năstac Lista dublu înlănțuită Recapitulare Într-o astfel de listă fiecare nod conţine doi pointeri: unul spre nodul următor şi unul spre nodul precedent.
SDA (PC2) Curs 9 Liste / Grafuri / Arbori Iulian Năstac Lista dublu înlănțuită Recapitulare Într-o astfel de listă fiecare nod conţine doi pointeri: unul spre nodul următor şi unul spre nodul precedent.
C:/Users/Lenovo/Dropbox/activitate matematica/cursuri/MS ETTI /msetti.dvi
 urs 4 Integrale curbilinii 4.1 Drumuri şi curbe Definiţie 4.1. O funcţie continuă γ : [a,b] R m se numeşte drum plan dacă m = 2 sau drum în spaţiu dacă m = 3. Punctul γ(a) se numeşte originea drumului,
urs 4 Integrale curbilinii 4.1 Drumuri şi curbe Definiţie 4.1. O funcţie continuă γ : [a,b] R m se numeşte drum plan dacă m = 2 sau drum în spaţiu dacă m = 3. Punctul γ(a) se numeşte originea drumului,
