Microsoft Word - 03 Dominica MOISE.doc
|
|
|
- Antoniu Tudor
- 4 ani în urmă
- Vzualizari:
Transcriere
1 CONFERINȚA NAȚIONALĂ DE INSTRUMENTAȚIE VIRTUALĂ, EDIȚIA A V-A, BUCURE TI, 20 MAI Pachet de programe care ilustrează capitole din matematică, fizică şi studiul fractalilor Luminița Dominica MOISE, Doina - Luminița DRUȚĂ Abstract. La conferinta din anul trecut am prezentat programele realizate de noi care ilustreaza geometria fractala. Am continuat crearea de programe in acest sens si am realizat in acest an scolar un studiu opțional Algoritmi, numere si fractali pentru elevii claselor a XI-a. Index Terms LabVIEW, prime numbers, chaos theory, fractals, dynamical systems. 1 INTRODUCERE În ultimii 30 de ani matematica şi ştiintele naturii au creat un domeniu nou care prin creativitatea şi puternica sa dezvoltare a devenit o ştiinţă de prim ordin. Fractalii şi teoria haosului au captivat atenţia unui public larg, aducând o nouă interpretare a lumii înconjurătoare. Acolo unde imprevizibilul, pe scurt haoticul a fost observat, noua ştiintă dă posibilitatea de a se vedea ordine şi structură. De asemenea, această teorie, făcănd conexiuni între domenii diferite ale activităţii umane, leagă matematica de viaţă. Utilizarea calculatorului - blamată de unii sau aprobată de alţii a deschis un nou capitol în evoluţia ştiinţei şi a dat speranţe în prelucrarea numărului mare de date şi relaţii necesare determinării evoluţiei unui sistem. Dar ştiinţele actuale au ajuns la concluzia unanimă că este imposibil să prevedem exact viitorul, deoarece determinismul strict şi evoluţia aparent accidentală nu se exclud reciproc, mai mult ele coabitează şi aceasta este o regulă a naturii. Teoria haosului şi geometria fractală se refera la acest ultim rezultat. 2 CONTINUTURI Ne-am propus prin studiul noilor capitole : Utilizarea algoritmilor si a conceptelor matematice in rezolvarea de probleme. Exprimarea coerenta in limbaj cotidian si formal a strategiilor de rezolvare a unei probleme. Luminita Dominica MOISE, Colegiul Tehnic TRAIAN Bucureşti,. dominic_moise@yahoo.com Doina Luminita DRUTA, Liceul bilingv DANTE ALIGHERI Bucureşti. doinadruta@yahoo.com Generalizarea unor proprieti prin modificarea contextului initial Prelucrarea datelor de tip cantitativ sau calitativ cuprinse in enunturi matematice. Modelarea matematica a unor contexte problematice. Pachetul de programe Fractall este structurat după continuturile optionalului Algoritmi, numere si fractali : 1. Numere pare şi impare - sau ce putem face cu doar două numere şi un algoritm. 2. Numere prime şi tabloul numerelor prime. 3. Demonstraţii fără cuvinte sau forţa de sugestie a unei imagini. 4. Puteri şi fractali. 5. Fractali din cercuri şi segmente. 6. Teorema lui Pitagora. 7. Sisteme dinamice. 8. Transformări în spaţii metrice. 3 TRANSFORMARI IN SPATII METRICE Ilustram in continuare pachetul Fractall cu programele din capitoul 8 -Transformari in spatii metrice- care are urmatoarea structura: a) Spaţii metrice: Definiţie, exemple; şiruri, transformări afine, funcţii continue. Spaţiul metric H(X). b) Principiul contracţiei în Spaţii metrice. c) Sisteme iterative. Algoritmul deterministic şi algoritmul iterativ probabilistic. d) O sursă de fractali: mulţimile invarante ale unor aplicaţii continue e) Mulţimi Julia ca atractori ai unor sisteme iterative f) Mulţimi de condensare si o teorema care modelează
2 14 CONFERINȚA NAȚIONALĂ DE INSTRUMENTAȚIE VIRTUALĂ, EDIȚIA A V-A, BUCURE TI, 20 MAI 2008 fractali. Contracţii în spaţii metrice Definiţie: Fie ( X, d ) un spaţiu metric şi f : X X o funcţie. f se numeste contracţie dacă exista k [0,1) astfel incat d(f(x),f(y) kd(x,y) oricare ar fi x, y X. Principiul contracţiei (Banach) Teorema : Fie (X,d) un spatiu metric complet si f: X X o contratie de factor k. Atunci: f are un unic punct fix u şi oricare ar fi x 0 X, şirul f (n) (x 0) converge la u. fig 1. Transformarea triunghiului lui Pascal prin funcţia (x, y) ( 10*x(x-9/10 ), y ) Fig 4.Transformarea succesivă a pătratului de latură 1 în urma unor contracţii SISTEMELE ITERATIVE (IFS) Operatorul Hutchinson 2 Considerăm R (planul euclidian) ca un spaţiu metric complet cu distanţa uzuală (euclidiană). Fie n un număr natural fixat (nenul) şi fie, pentru orice 2 2 j { 1,2,..., n}, o contracţie W j : R R având k j. Dacă A este o submulţime 2 R, notăm cu W j (A) imaginea mulţimii factorul de contracţie oarecare din A prin funcţia W j. Definim aplicaţia (operatorul lui Hutchinson): H : H(R 2 ) H(R 2 ),H(A)=W 1 (A)U W 2 (A)U... U W n (A). Vom nota,,..., ) H = W W W. ( 1 2 n fig 2. Transformarea triunghiului lui Pascal prin funcţia (x,y) (x 2 - y 2,2xy ) 1200 de linii sunt în domeniul de definiţie (0; 3) De asemenea (R 2,W 1,W 2,...,W n) se numeste sistem iterativ de funcţii (IFS) 2 Observatie: Se poate înlocui în definiţie R cu X un spaţiu metric complet. Este adevărată următoarea afirmaţie: Teoremă: Operatorul lui Hutchinson este o contracţie pe spaţiul metric complet al părţilor compacte din plan H(R 2 ) cu distanţa Hausdorff. În plus, factorul de contracţie al lui H este cel mai mare element al mulţimii k, k,..., k } k. { 1 2 n fig 3.Transformarea unui pătrat de latură 1 Definiţie: Punctul fix F H(R 2 ) al operatorului Hutchinson (există şi este unic conform principiului contracţiei) se numeşte atractor al sistemului iterativ (sau fractal deterministic) şi este limita şirului H n (A), oricare ar fi A H(R 2 )
3 L.D. MOISE, D.L. DRUȚĂ - PACHET DE PROGRAME CARE ILUSTREAZĂ CAPITOLE DIN MATEMATICĂ, FIZICĂ I STUDIUL FRACTALILOR 15 Exemplul 1 :trei contracţii de coeficient ½ H=(W 1,W 2,W 3) W 1 =omotetie de factor ½ urmata de o translaţie, W 2=omotetie de factor ½ urmata de o translaţie W 3=omotetie de factor ½, A= pătratul de latură 1. Vom genera triunghiul lui Sierpinski ca atractor al unui sistem iterativ Fig 5. triunghiul lui Sierpinski ca atractor al unui sistem iterativ prnind de la un patrat Exemplul 2 : trei contracţii de coeficient ½ H=(W 1,W 2,W 3) W 1 = omotetie de factor ½, W 2 = omotetie de factor ½ urmată de o translaţie W 3 = omotetie de factor ½ urmată de o translaţie A = triunghiul din prima imagine Fig 6. triunghiul lui Sierpinski ca atractor al unui sistem iterativ pornind de la un triunghi
4 16 CONFERINȚA NAȚIONALĂ DE INSTRUMENTAȚIE VIRTUALĂ, EDIȚIA A V-A, BUCURE TI, 20 MAI 2008 Exemplul 3: opt contracţii de coeficient 1/3 H=(W 1,W 2,...,W 8 ) A= pătrat de latură l=1 Fig7. covorul lui Sierpinski ca atractor al unui sistem iterativ prnind de la un patrat Exemplul 4 : trei contracţii de tip ferigă (vezi paragraful următor) H=(W 1,W 2,W 3) A = pătrat plin (sau doar un punct) fig 8. feriga ca atractor
5 L.D. MOISE, D.L. DRUȚĂ - PACHET DE PROGRAME CARE ILUSTREAZĂ CAPITOLE DIN MATEMATICĂ, FIZICĂ I STUDIUL FRACTALILOR 17 Algoritmul iterativ probabilistic Sistemele iterative (IFS) considerate anterior sunt deterministe în sensul că fiecare iteraţie este unic determinată. Se pot considera sisteme iterative care au un caracter aleator (haotic) în sensul că o anumită iteraţie este aleasă dintr-o listă de posibili operatori (fiecare cu o anumită probabilitate). Exemplul 1: Vom efectua de iteraţii în felul următor: se obţine aleator un număr pozitiv subunitar şi în funcţie de acest număr se va face una din transformările 1, 2 sau 3 cu probabilităţi egale (p1=0.33 p2=0.33, p3=0.34). Pornind de la un punct arbitrar obţinem: Exemplul 2: Observăm că de fapt prima funcţie aplicată unui punct M transformă punctul în mijlocul segmentului OM unde O este originea axelor de coordomate O(0,0) Cea de a doua transformare determină mijlocul segmentului ce uneşte punctual dat M cu cel de-al doilea vârf al triunghiului. La fel pentru cea de a treia tranformare. Înlocuind cele trei transformări anterioare conform cu interpretarea geometrică anterioară obţinem algoritmul probabilistic al triunghiului lui Sierpinki pentru un triunghi oarecare. fig 9.triunghiul lui Sierpinski- algoritm iterativ probabilistic Exemplul 3: Putem face 4 transformări diferite ale unui pătrat ca în imaginea următoare : fig 10. transformari de tip feriga
6 18 CONFERINȚA NAȚIONALĂ DE INSTRUMENTAȚIE VIRTUALĂ, EDIȚIA A V-A, BUCURE TI, 20 MAI 2008 Mulţimi Julia ca atractori ai unor sisteme iterative In acest capitol, primul exemplu a condus la generarea triunghiului lui Sierpinski ca atractor al unui sistem iterativ de funcţii (R 2, W 1,W 2,W 3). Expresia analitică a celor trei funcţii ale sistemului este: H= ( W 1, W 2, W 3, W 4 ) Fig 11. feriga- algoritm iterativ probabilistic Mai mult f( )=. Observaţie: dacă (x,y), calculând cu calculatorul orbita şirului vor rezulta puncte care nu aparţin datorită erorilor de calcul; de aceea în reprezentarea următoare ne luăm o marjă de siguranţă. W 1 (x,y)=(0.5x, 0.5y+0.5) W 2(x,y)=(0.5x+0.5, 0.5y) W 3(x,y)=(0.5x, 0.5y) Acest sistem iterativ de funcţii este direct legat de sistemul dinamic (R 2, f ) unde Să reprezentăm multimea Julia a sistemului dinamic (R 2, f ): punctele din pătratul de latură unu ale căror orbite nu converg la infinit. Vom reprezenta punctele (x,y) cu 0 x 1, 0 y 1 ale căror orbite verifică relaţia : x 2 +y pentru primele10 iteraţii. Vom obtine o noua generare a triunghiului lui Sierppinski prin algoritmul escape-time Se poate demonstra că pentru x R 2, orbita şirului x n =f n (x) converge la infinit, adică d ( O, f n (x)) pentru n. Sistemul dinamic (R 2, f ) verifică relaţia d (f(x 1),f(x 2 )) =2d(x 1, x 2), deci distanţa imaginilor prin f este dublul distanţei dintre puncte initiale. Intuitiv ne asteptăm ca punctele apropiate de să conveargă mai lent la infinit decât cele mai îndepărtate. Cât de repede diverg aceste orbite? Ne propunem să realizam o imagine care să ilustreze acest lucru. Dacă punctul părăseşte discul de rază r 2 =200 (x 2 +y 2 200) după prima iteraţie îl colorăm cu culoarea 1.Dacă punctul părăseşte discul de rază r 2 =200 (x 2 +y 2 200) după a doua iteraţie îl colorăm cu culoarea 2 ş.a.m.d
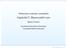
7 L.D. MOISE, D.L. DRUȚĂ - PACHET DE PROGRAME CARE ILUSTREAZĂ CAPITOLE DIN MATEMATICĂ, FIZICĂ I STUDIUL FRACTALILOR 19 Vom repeta algoritmul si pentru doua din multimile Julia prezentate in capitolul precedent: Fig12. Triunghiul lui Sierpinski prin algoritmul escape-time fig 13. multimi Julia asociate functiei f(x)=x 2 +c fig 143. Diagrama programului care a generat imaginea din figura 12.
8 20 CONFERINȚA NAȚIONALĂ DE INSTRUMENTAȚIE VIRTUALĂ, EDIȚIA A V-A, BUCURE TI, 20 MAI 2008 Fig 15. Capturi de acran ale pachetului de programe Fractall
9 L.D. MOISE, D.L. DRUŢĂ - PACHET DE PROGRAME CARE ILUSTREAZĂ CAPITOLE DIN MATEMATICĂ, FIZICĂ I STUDIUL FRACTALILOR 21 BIBLIOGRAFIE 1) 2) 3) Michael F.Barnsley Fractals every where Second Edition, Academic Press Professional, Heinz Otto Peitgen, Harmut Jurgens, Dietmar Saupe Chaos and New frontiers of science Springer Verlag Tom Savu, Neacşu Ion, Grigorescu Ştefan, Garabet Elena Mihaela, Bazele instrumentaţiei virtuale LabView, Editura Atelier didactic, Bucureşti, ) Robert L.Devamy Chaos, Fractals and Dynamics Wesley Publishing Company, ) Ioan Odăgescu, Ion Smeureanu, Daniel Luca,Marian Dârdală, Felix Furtună Grafică interactivă pe calculatorul personal Editura Militară, Bucureşti ) Mircea Olteanu- Fractali curs universitar, Universitatea Politehnica din Bucureşti 7) Dominica Moise, Brandusa Bogdan, Doina Druta Algoritmi, numere si fractali, editura Printech, Bucuresti, 2007
Distanţa euclidiană (indusă de norma euclidiană) (în R k ). Introducem în continuare o altă aplicaţie, de această dată pe produsul cartezian R k XR k,
Distanţa euclidiană (indusă de norma euclidiană) (în R k ). Introducem în continuare o altă aplicaţie, de această dată pe produsul cartezian R k XR k, aplicaţie despre care vom vedea că reprezintă generalizarea
Pachete de lecţii disponibile pentru platforma AeL
Pachete de lecţii disponibile pentru platforma AeL -disciplina Matematică- Nr. crt Nume pachet clasa Nr. momente Nr.Recomandat de ore 1 Corpuri geometrice V 6 1 2 Fracţii V 14 5 3 Măsurarea lungimilor.
Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică Gheorghe Asachi Iaşi, 2015 Analiză Matematică Lucian Maticiuc 1 / 29
Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică Gheorghe Asachi Iaşi, 2015 Analiză Matematică Lucian Maticiuc 1 / 29 Definiţie. Şiruri mărginite. Şiruri monotone. Subşiruri ale
DAN LASCU ADRIANA-LIGIA SPORIŞ ANDA OLTEANU PAUL VASILIU MATEMATICĂ. CULEGERE DE PROBLEME TIP GRILĂ PENTRU ADMITEREA ÎN ACADEMIA NAVALĂ MIRCEA CEL BĂT
DAN LASCU ADRIANA-LIGIA SPORIŞ ANDA OLTEANU PAUL VASILIU MATEMATICĂ. CULEGERE DE PROBLEME TIP GRILĂ PENTRU ADMITEREA ÎN ACADEMIA NAVALĂ MIRCEA CEL BĂTRÂN Colecţia Matematică DAN LASCU ADRIANA-LIGIA SPORIŞ
Gheorghe IUREA Adrian ZANOSCHI algebră geometrie clasa a VII-a ediţia a V-a, revizuită mate 2000 standard EDITURA PARALELA 45 Matematică. Clasa a VII-
Gheorghe IUREA Adrian ZANOSCHI algebră geometrie clasa a VII-a ediţia a V-a, revizuită mate 2000 standard 3 Algebră Capitolul I. MULŢIMEA NUMERELOR RAŢIONALE Identificarea caracteristicilor numerelor raţionale
Cursul 8 Funcţii analitice Vom studia acum comportarea şirurilor şi seriilor de funcţii olomorfe, cu scopul de a dezvălui o proprietate esenţială a ac
Cursul 8 Funcţii analitice Vom studia acum comportarea şirurilor şi seriilor de funcţii olomorfe, cu scopul de a dezvălui o proprietate esenţială a acestor funcţii: analiticitatea. Ştim deja că, spre deosebire
Cursul 14 Mulţimea lui Mandelbrot Mulţimile şi funcţiile cu caracter excepţional (mulţimea lui Cantor, insula lui Koch, funcţiile lui Weierstrass şi T
Cursul 14 Mulţimea lui Mandelbrot Mulţimile şi funcţiile cu caracter excepţional (mulţimea lui Cantor, insula lui Koch, funcţiile lui Weierstrass şi Takagi, curbele lui Peano, mulţimile Julia, ş.a.) au
Prelegerea 4 În această prelegere vom învăţa despre: Algebre booleene; Funcţii booleene; Mintermi şi cuburi n - dimensionale. 4.1 Definirea algebrelor
Prelegerea 4 În această prelegere vom învăţa despre: Algebre booleene; Funcţii booleene; Mintermi şi cuburi n - dimensionale. 4.1 Definirea algebrelor booleene Definiţia 4.1 Se numeşte algebră Boole (booleană)
D.Rusu, Teoria măsurii şi integrala Lebesgue 6 MĂSURA LEBESGUE Cursul 5 Teorema 6.26 Există submulţimi ale lui R care nu sunt măsurabile Lebesgue. Dem
D.Rusu, Teoria măsurii şi integrala Lebesgue 6 MĂSURA LEBESGUE Cursul 5 Teorema 6.26 Există submulţimi ale lui R care nu sunt măsurabile Lebesgue. Demonstraţie. Fie mulţimea A = [0, ], pe care definim
Cursul 12 (plan de curs) Integrale prime 1 Sisteme diferenţiale autonome. Spaţiul fazelor. Fie Ω R n o mulţime deschisă şi f : Ω R n R n o funcţie de
Cursul 12 (plan de curs) Integrale prime 1 Sisteme diferenţiale autonome. Spaţiul fazelor. Fie Ω R n o mulţime deschisă şi f : Ω R n R n o funcţie de clasă C 1. Vom considera sistemul diferenţial x = f(x),
Microsoft Word - Programa finala olimpiadei matematica 2007 gimnaziu.doc
ROMÂNIA MINISTERUL EDUCAŢIEI ŞI CERCETĂRII DIRECŢIA GENERALĂ ÎNVĂŢĂMÂNT PREUNIVERSITAR SERVICIUL NAŢIONAL DE EVALUARE ŞI EXAMINARE PROGRAMA OLIMPIADEI DE MATEMATICĂ CLASELE V XII AN ŞCOLAR 006 / 007 Pentru
Capitolul MD. 10 Metoda funcţiilor Liapunov Fie sistemul diferenţial x = f (t, x), t t 0, x D R n. (10.1) Presupunem că x = 0 este punct de echilibru,
Capitolul MD. 10 Metoda funcţiilor Liapunov Fie sistemul diferenţial x = f (t, x), t t 0, x D R n. (10.1) Presupunem că x = 0 este punct de echilibru, adică f (t, 0) = 0, t t 0. In acest paragraf, funcţia
RecMat dvi
Conice şi cubice în probleme elementare de loc geometric Ştefan DOMINTE 1 Abstract. In this Note, a number of simple problems are presented to support the idea that conic and cubic curves can frequently
Cursul 10 Fractali de tip Newton Vom prezenta în continuare o nouă modalitate de generare a fractalilor, modalitate care îşi are originea într-o probl
Cursul 10 Fractali de tip Newton Vom prezenta în continuare o nouă modalitate de generare a fractalilor, modalitate care îşi are originea într-o problemă formulată în anul 1879 de Arthur Cayley (1821 1895)
Facultatea de Matematică Anul II Master, Geometrie Algebrică Mulţimi algebrice ireductibile. Dimensiune 1 Mulţimi ireductibile Propoziţia 1.1. Fie X u
Facultatea de Matematică Anul II Master, Geometrie Algebrică Mulţimi algebrice ireductibile. Dimensiune 1 Mulţimi ireductibile Propoziţia 1.1. Fie X un spaţiu topologic. Următoarele afirma-ţii sunt echivalente:
Cursul 6 Cadru topologic pentru R n În continuarea precedentei părţi, din cursul 5, dedicată, în întregime, unor aspecte de ordin algebric (relative l
Cursul 6 Cadru topologic pentru R n În continuarea precedentei părţi, din cursul 5, dedicată, în întregime, unor aspecte de ordin algebric (relative la R n, în principal), sunt prezentate aici elemente
Examenul de bacalaureat 2012
CENTRUL NAŢIONAL DE EVALUARE ŞI EXAMINARE PROGRAMA DE EXAMEN PENTRU DISCIPLINA MATEMATICĂ BACALAUREAT 2015 PROGRAMA M_tehnologic Filiera tehnologică, profilul servicii, toate calificările profesionale,
Cursul 13 Mulţimi Julia Fie f : C C o funcţie complexă şi fie f n = f f f iterata de ordin n a lui f. Peste tot în continuare vom presupune că f este
Cursul 13 Mulţimi Julia Fie f : C C o funcţie complexă şi fie f n = f f f iterata de ordin n a lui f. Peste tot în continuare vom presupune că f este dezvoltabilă în serie de puteri în tot planul (cum
Cursul 12 Şiruri recurente în planul complex Vom studia, în continuare, comportarea în raport cu data iniţială a şirurilor definite prin relaţii de re
Cursul 12 Şiruri recurente în planul complex Vom studia, în continuare, comportarea în raport cu data iniţială a şirurilor definite prin relaţii de recurenţă de forma z n+1 = f(z n ), n = 0, 1, 2,...,
TEORIA MĂSURII Liviu C. Florescu Universitatea Al.I.Cuza, Facultatea de Matematică, Bd. Carol I, 11, R Iaşi, ROMANIA, e mail:
TEORI MĂSURII Liviu C. Florescu Universitatea l.i.cuza, Facultatea de Matematică, Bd. Carol I, 11, R 700506 Iaşi, ROMNI, e mail: lflo@uaic.ro În mod intenţionat această pagină este lăsată albă! Cuprins
Tiberiu Trif Analiză matematică 2 Calcul diferențial și integral în R n
Tiberiu Trif Analiză matematică 2 Calcul diferențial și integral în R n Cuprins Notații v 1 Topologie în R n 1 1.1 Spațiul euclidian R n........................ 1 1.2 Structura topologică a spațiului
FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituţia de învăţământ superior Universitatea Alexandru Ioan Cuza din Iaşi 1.2 Facultatea Facultatea de
FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituţia de învăţământ superior Universitatea Alexandru Ioan Cuza din Iaşi 1.2 Facultatea Facultatea de Matematică 1.3 Departamentul Matematică Didactic 1.4
Şcoala ………
Şcoala... Clasa a X-a Disciplina: Matematică TC + CD Anul şcolar: 07-08 TC = trunchi comun 35 săptămâni: 8 săptămâni semestrul I CD = curriculum diferenţiat Nr. ore: 3 ore / săptămână 7 săptămâni semestrul
DOMENIUL: Matematica
PLAN DE ÎNVĂŢĂMÂNT valabil începând cu anul universitar 2013-2014 Program postuniversitar de conversie profesională Facultatea: MATEMATICĂ ȘI INFORMATICĂ Programul de studii: MATEMATICĂ Forma de învățământ:
MergedFile
PROIECT DIDACTIC Clasa a VII-a Matematică Proiect didactic realizat în cadrul programului - pilot Digitaliada, revizuit de Simona Roșu, profesor Digitaliada Textul și ilustrațiile din acest document începând
I
METODA VECTORIALĂ ÎN GEOMETRIE prof. Andrei - Octavian Dobre Această metodă poate fi descrisă după cum urmează: Fiind dată o problemă de geometrie, după explicitarea şi reprezentarea grafică a configuraţiei
BAC 2007 Pro Didactica Programa M1 2 Rezolvarea variantei 36 versiune finală Redactia Pro Didactica Suportul pe net:
BAC 27 Pro Didactica Programa M1 2 Rezolvarea variantei 36 versiune finală Redactia Pro Didactica Suportul pe net: http://www./ CAPITOLUL 1 Varianta 36 1. Subiectul I. (a) Avem 2 ( ) 2+ ( ) 2= 7i = 2 7
Prezentarea cursului Didactica Matematicii Oana Constantinescu
Prezentarea cursului Didactica Matematicii Oana Constantinescu Didactica este stiinta conducerii procesului de predare-invatare-evaluare. Ea studiaza procesul de invatare in ansamblul sau, pe toate treptele
Microsoft Word - Matematika_kozep_irasbeli_jav_utmut0513V28_roman.doc
Matematika román nyelven középszint 0513 ÉRETTSÉGI VIZSGA 005. május 8. MATEMATIKA ROMÁN NYELVEN MATEMATICĂ KÖZÉPSZINTŰ ÉRETTSÉGI VIZSGA EXAMEN DE BACALAUREAT NIVEL MEDIU Az írásbeli vizsga időtartama:
Lucian L. TURDEANU Georgeta D. POP (MANEA) BAZELE GEOMETRICE ALE FOTOGRAMETRIEI CONSPRESS BUCUREŞTI 2009
Lucian L. TURDEANU Georgeta D. POP (MANEA) BAZELE GEOMETRICE ALE FOTOGRAMETRIEI CONSPRESS BUCUREŞTI 2009 CUPRINS Pg. INTRODUCERE. Noţiuni preliminare (L. Turdeanu, G. Pop)... 6 Probleme... 11 1. GEOMETRIA
FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituţia de învăţământ superior Universitatea Alexandru Ioan Cuza din Iaşi 1.2 Facultatea Facultatea de
FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituţia de învăţământ superior Universitatea Alexandru Ioan Cuza din Iaşi 1.2 Facultatea Facultatea de Matematică 1.3 Departamentul Matematică Didactic 1.4
Microsoft Word - Algoritmi genetici.docx
1.1 Generalităţi Algoritmii genetici fac parte din categoria algoritmilor de calcul evoluționist și sunt inspirați de teoria lui Darwin asupra evoluției. Idea calculului evoluționist a fost introdusă în
Modelarea si Simularea Sistemelor de Calcul
Modelarea şi Simularea Sistemelor de Calcul Generarea de numere aleatoare ( lab. 5) Numim variabilă aleatoare acea funcţie X : (Ω, δ, P) R, care în cazul mai multor experimente efectuate în condiţii identice
Prelegerea 3 În această prelegere vom învăţa despre: Clase speciale de latici: complementate. modulare, metrice, distributive şi 3.1 Semi-distributivi
Prelegerea 3 În această prelegere vom învăţa despre: Clase speciale de latici: complementate. modulare, metrice, distributive şi 3.1 Semi-distributivitate şi semi - modularitate Fie L o latice. Se numeşte
Analiz¼a Matematic¼a - Curs 6 M¼ad¼alina Roxana Buneci
Analiz¼a Matematic¼a - Curs 6 M¼ad¼alina Roxana Buneci Cuprins 4 Spaţii topologice (continuare din cursul 5) 3 4.6 Spaţiul R n............................ 3 5 Calcul diferenţial 7 5. Derivatele funcţiilor
MD.09. Teoria stabilităţii 1
MD.09. Teoria stabilităţii 1 Capitolul MD.09. Teoria stabilităţii Cuvinte cheie Soluţie stabilă spre +, instabilă si asimptotic stabilă, punct de echilibru, soluţie staţionară, stabilitatea soluţiei banale,
CLP_UTCN-grila-2012.dvi
Liceul: Numele: Punctaj: Prenumele: Concursul liceelor partenere cu Universitatea Tehnică din Cluj-Napoca Test grilă Ediţia a treia mai 0 Clasa a X-a În casuţa din stânga întrebării se va scrie litera
Noțiuni matematice de bază
Sistem cartezian definitie. Coordonate carteziene Sistem cartezian definiţie Un sistem cartezian de coordonate (coordonatele carteziene) reprezintă un sistem de coordonate plane ce permit determinarea
matematica
MINISTERUL EDUCAŢIEI, CERCETĂRII ŞI INOVĂRII PROGRAMĂ ŞCOLARĂ M A T E M A T I C Ă CLASA A IX-A CICLUL INFERIOR AL LICEULUI Aprobată prin ordin al ministrului nr. / Bucureşti, 2009 NOTĂ DE PREZENTARE În
COMENTARII FAZA JUDEŢEANĂ, 9 MARTIE 2013 Abstract. Personal comments on some of the problems presented at the District Round of the National Mathemati
COMENTARII FAZA JUDEŢEANĂ, 9 MARTIE 2013 Abstract. Personal comments on some of the problems presented at the District Round of the National Mathematics Olympiad 2013. Data: 12 martie 2013. Autor: Dan
CURBE BÉZIER În CAGD se utilizează adesea curbele polinomiale, adică acele curbe definite de o parametrizare polinomială: C : [a, b] R 3 C(t) = (x(t),
![CURBE BÉZIER În CAGD se utilizează adesea curbele polinomiale, adică acele curbe definite de o parametrizare polinomială: C : [a, b] R 3 C(t) = (x(t),](/thumbs/101/150500936.jpg "CURBE BÉZIER În CAGD se utilizează adesea curbele polinomiale, adică acele curbe definite de o parametrizare polinomială: C : [a, b] R 3 C(t) = (x(t),")
CURE ÉZIER În CAGD se utilizează adesea curbele polinomiale, adică acele curbe definite de o parametrizare polinomială: C : [a, b] R 3 C(t) = (x(t), y(t), z(t)) cu x, y, z polinoame de grad n. Maximul
Microsoft Word - cap1p4.doc
Algebră liniară, geometrie analitică şi diferenţială.6 Subspaţii vectoriale Fie V un spaţiu vectorial peste corpul K. În cele ce urmează vom introduce două definiţii echivalente pentru noţiunea de subspaţiu
Microsoft Word - Cap09_AutoorganizareSiEmergentaInSistemeleAdaptiveComplexe_grile.doc
Grile 1. Care este proprietatea universală în sistemele vii, organizaţii şi sisteme economice şi sociale, cărora le conferă calitatea de a manifesta caracteristici şi comportamente cu totul noi, care nu
Microsoft Word - proiect 2013
13 4 Temă de proiect TCM, an universitar 2012-2013 Se consideră mecanismul cu camă-tachet axat din Fig. 1. Elementul conducător este cama plana 1, care are profilul un cerc cu raza r=0,072 m. Axa A a cuplei
PROGRAMA CONCURSULUI NAŢIONAL
ANUL ŞCOLAR 2011-2012 CLASA a IX-a În programa de concurs pentru clasa a IX-a sunt incluse conţinuturile programelor din clasele anterioare şi din etapele anterioare. 1. Mulţimi şi elemente de logică matematică.
Universitatea Lucian Blaga Sibiu Facultatea de inginerie-Departamentul de calculatoare şi Inginerie Electrică Titular curs: Şef lucrări dr.mat. Po
Titular curs: Şef lucrări dr.mat. Pop N.Daniel Laborator : Şef lucrări dr.mat. Pop N.Daniel Fiecare dintre noi foloseste cuvântul probabil in limbajul curent de câteva ori pe zi, atunci când se referă
Geometrie afină Conf. Univ. Dr. Cornel Pintea cpintea math.ubbcluj.ro Cuprins 1 Săptămâna Endomorfismele unui spaţiu afin Transla
Geometrie afină Conf Univ Dr Cornel Pintea E-mail: cpintea mathubbclujro Cuprins 1 Săptămâna 12 1 2 Endomorfismele unui spaţiu afin 1 21 Translaţia 1 22 Subspaţii invariante 2 23 Omotetii 2 3 Apendix 2
Logică și structuri discrete Relații. Funcții parțiale Marius Minea marius/curs/lsd/ 20 octombrie 2014
Logică și structuri discrete Relații. Funcții parțiale Marius Minea marius@cs.upt.ro http://www.cs.upt.ro/ marius/curs/lsd/ 20 octombrie 2014 Relații în lumea reală și informatică Noțiunea matematică de
matematica, liceu-specializ. matematica-informatica
Anexa 2 la ordinul ministrului educaţiei şi cercetării nr. 3252/ 13.02.2006 MINISTERUL EDUCAŢIEI ŞI CERCETĂRII CONSILIUL NAŢIONAL PENTRU CURRICULUM PROGRAME ŞCOLARE PENTRU CICLUL SUPERIOR AL LICEULUI MATEMATICĂ
METODE NUMERICE ÎN INGINERIE
METODE NUMERICE ÎN INGINERIE REZOLVAREA NUMERICĂ A SISTEMELOR DE ECUATII LINIARE Aspecte generale (1) (2) (3) (4) (5) Unicitatea soluţiei Un sistem de ecuaţii liniare are o soluţie unică numai dacă matricea
PAS cap. 2: Reprezentări rare p. 1/35 Prelucrarea avansată a semnalelor Capitolul 2: Reprezentări rare Bogdan Dumitrescu Facultatea de Automatică şi C
PAS cap. 2: Reprezentări rare p. 1/35 Prelucrarea avansată a semnalelor Capitolul 2: Reprezentări rare Bogdan Dumitrescu Facultatea de Automatică şi Calculatoare Universitatea Politehnica Bucureşti PAS
Microsoft Word - 4_Fd_Teoria_sist_I_2013_2014_MLF_Calc
FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituţia de învăţământ superior Universitatea Sapientia din Cluj-Napoca 1.2 Facultatea Ştiinţe Tehnice şi Umaniste 1.3 Departamentul Inginerie Mecanică 1.4
PowerPoint Presentation
ELEMENTE DE MORFOLOGIE MATEMATICA Morfologia matematica Cadru de abordare diferit: Pana acum : Imaginea este o functie de doua variabile. Pixelii imaginii (valori si coordonate de pozitie) sunt structurati
Clasa IX 1. O lăcustă face salturi, fiecare salt în linie dreaptă şi de două ori mai lung ca precedentul. Poate vreodată lăcusta să revină în punctul
Clasa IX. O lăcustă face salturi, fiecare salt în linie dreaptă şi de două ori mai lung ca precedentul. Poate vreodată lăcusta să revină în punctul de plecare iniţial? Soluţie. Răspunsul este negativ.
Microsoft Word - Programa_Evaluare_Nationala_2011_Matematica.doc
C E N T R U L NAłIONAL DE EVALUARE ŞI E X A M I N A R E PROGRAMA PENTRU DISCIPLINA MATEMATICĂ EVALUAREA NAłIONALĂ PENTRU ELEVII CLASEI A VIII A Pagina 1 din 5 PROGRAMA PENTRU DISCIPLINA MATEMATICĂ I. STATUTUL
CONCURSUL NAŢIONAL DE MATEMATICA PANAITOPOL EDIŢIA a X-a, TULCEA, 21 aprilie 2018 Clasa a VII - a 1. Se consideră numerele reale x, y şi z, cel puţin
CONCURSUL NAŢIONAL DE MATEMATICA PANAITOPOL EDIŢIA a X-a, TULCEA, 21 aprilie 2018 Clasa a VII - a 1. Se consideră numerele reale x, y şi z, cel puţin două dintre ele fiind diferite. Arătaţi că x y z 0
0 Probleme pentru pregătirea examenului final la Analiză Matematică 1. Să se calculeze următoarele integrale improprii: dx a) x 4 ; b) x 3 dx dx
Probleme pentru pregătirea examenului final la Analiză Matematică. ă se calculeze următoarele integrale improprii: dx a) + x ; b) x dx dx; c) + x x + x ) ; dx x d) x + x ) ; e) dx; f) x p e xq dx, p >,
MergedFile
PROIECT DIDACTIC Clasa a VI-a Matematică Proiect didactic realizat de Nicoleta Popa, profesor Digitaliada, revizuit de Ioan Popa, profesor Digitaliada Textul și ilustrațiile din acest document începând
Aero-BCD, , Prof. L. Costache & M. Olteanu Notițe de Adrian Manea Seminar 5 Șiruri și serii de funcții. Serii de puteri 1 Șiruri de funcții D
Seminar 5 Șiruri și serii de funcții. Serii de puteri Șiruri de funcții Definiţie.: Fie (f n ) n un șir de funcții, cu fiecare f n : [a, b] R și fie o funcție f : [a, b] R. PC Spunem că șirul (f n ) converge
15. Logică matematică cu aplicații în informatică - MI 3
FIȘA DISCIPLINEI 1. Date despre program 1.1. Instituția de învățământ superior Universitatea de Vest din Timișoara 1.2. Facultatea Matematică și Informatică 1.3. Departamentul Matematică 1.4. Domeniul
Microsoft Word - D_ MT1_II_001.doc
,1 SUBIECTUL II (30p) Varianta 1001 a b 1 Se consideră matricea A = b a, cu a, b şi 0 http://wwwpro-matematicaro a) Să se arate că dacă matricea X M ( ) verifică relaţia AX = XA, atunci există uv,, astfel
PROBLEME PRIVIND INSTABILITATEA UNOR CALCULE ALE MECANISMELOR
INSTABILITĂŢI DE CALCUL LA ANALIZA DIADEI RRR s.l. univ. dr. ing. Valentina MANEA s.l.univ.dr.ing. Raluca GRASU Rezumat. Se studiază instabilităţile de calcul care apar la analiza diadei RRR, cauzate de
Microsoft Word - 2 Filtre neliniare.doc
20 Capitolul 2 - Filtre neliniare 21 CAPITOLUL 2 FILTRE NELINIARE 2-1. PRELIMINARII Răspunsul la impuls determină capacitatea filtrului de a elimina zgomotul de impulsuri. Un filtru cu răspunsul la impuls
Matematica VI
There are no translations available. Datorita unor probleme tehnice, site-ul nu poate fi vizionat cu Internet Explorer 8, partea de teste (apare pagina alba). Pentru navigare, va recomandam Chrome, Mozilla,
Microsoft Word - matem_aplicate in Economie aa FD Bala.doc
FIŞA DISCIPLINEI ANUL UNIVERSITAR 05-06. DATE DESPRE PROGRAM. Instituţia de învăţământ superior UNIVERSITATEA DIN CRAIOVA. Facultatea Economie și Administrarea Afacerilor.3 Departamentul Management, Marketing
Universitatea Politehnica din Bucureşti 2019 Disciplina: Geometrie şi Trigonometrie G1 * Varianta A 1. Ştiind cos x = 3 2, atunci sin2 x
1 5 6 7 Universitatea Politehnica din Bucureşti 019 Disciplina: Geometrie şi Trigonometrie G1 * Varianta A 1 Ştiind cos x atunci sin x este: (6 pct a 1 ; b 1 ; c 1 ; d ; e 1 8 ; f Soluţie Folosind prima
Microsoft Word - TIC5
CAPACITATEA CANALELOR DE COMUNICAŢIE CAPITOLUL 5 CAPACITATEA CANALELOR DE COMUNICAŢIE În Capitolul 3, am văzut că putem utiliza codarea sursă pentru a reduce redundanţa inerentă a unei surse de informaţie
LOGICA MATEMATICA SI COMPUTATIONALA Sem. I,
LOGICA MATEMATICĂ ŞI COMPUTAŢIONALĂ Sem. I, 2017-2018 Ioana Leustean FMI, UB Partea III Calculul propoziţional clasic Consistenţă şi satisfiabilitate Teorema de completitudine Algebra Lindenbaum-Tarski
02. Analiza matematica 3 - MI 2
FIȘA DISCIPLINEI 1. Date despre program 1.1. Instituția de învățământ superior Universitatea de Vest din Timișoara 1.2. Facultatea Matematică și Informatică 1.3. Departamentul Matematică 1.4. Domeniul
Cursul 7 Formula integrală a lui Cauchy Am demonstrat în cursul precedent că, dacă D C un domeniu simplu conex şi f : D C o funcţie olomorfă cu f cont
Cursul 7 Formula integrală a lui Cauchy Am demonstrat în cursul precedent că, dacă D C un domeniu simplu conex şi f : D C o funcţie olomorfă cu f continuă pe D, atunci, pe orice curbă rectificabilă şi
FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituţia de învăţământ superior Universitatea Alexandru Ioan Cuza din Iaşi 1.2 Facultatea Facultatea de
FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituţia de învăţământ superior Universitatea Alexandru Ioan Cuza din Iaşi 1.2 Facultatea Facultatea de Matematică 1.3 Departamentul Matematică Didactic 1.4
Clustere şi impurităţi în sisteme complexe
C: Soluţii numerice ale ecuaţiei Schrödinger independentă de timp. Metoda Tirului BIBLIOGRAFIE Ion. I. Cotaescu. Curs de Mecanica Cuantică, Tipografia UVT 990 Epperson J, An introduction to numerical methods
Examenul de bacalaureat 2012
PROGRAMA PENTRU SIMULAREA EXAMENULUI DE BACALAUREAT 2019 LA DISCIPLINA MATEMATICĂ În cadrul examenului de Bacalaureat 2019, Programele de examen la disciplina Matematica se diferenţiază în funcţie de filiera,
Logică și structuri discrete Limbaje regulate și automate Marius Minea marius/curs/lsd/ 24 noiembrie 2014
Logică și structuri discrete Limbaje regulate și automate Marius Minea marius@cs.upt.ro http://www.cs.upt.ro/ marius/curs/lsd/ 24 noiembrie 2014 Un exemplu: automatul de cafea acțiuni (utilizator): introdu
Examenul de bacalaureat 2012
INSPECTORATUL Ș C O L A R J U D E Ț E A N C O V A S N A PROGRAMA PENTRU SIMULAREA EXAMENULUI DE BACALAUREAT 2015 LA DISCIPLINA MATEMATICĂ În cadrul examenului de Bacalaureat 2015, Programele de examen
PROGRAMĂ OPŢIONAL CLASA a VII-a CONSTRUCŢII GEOMETRICE CU RIGLA ŞI COMPASUL ARIA CURRICULARĂ: MATEMATICĂ ŞI ŞTIINŢE PROFESOR, IOJA IOAN
PROGRAMĂ OPŢIONAL CLASA a VII-a CONSTRUCŢII GEOMETRICE CU RIGLA ŞI COMPASUL ARIA CURRICULARĂ: MATEMATICĂ ŞI ŞTIINŢE PROFESOR, IOJA IOAN Argument Construcţiile geometrice au constituit partea principală
Dorel LUCHIAN Gabriel POPA Adrian ZANOSCHI Gheorghe IUREA algebră geometrie clasa a VIII-a ediţia a V-a, revizuită mate 2000 standard EDITURA PARALELA
Dorel LUCHIAN Gabriel POPA Adrian ZANOSCHI Gheorghe IUREA algebră geometrie clasa a VIII-a ediţia a V-a, revizuită mate 000 standard 3 10 PP Algebră Capitolul I. NUMERE REALE Competenţe specifice: Determinarea
..MINISTERUL EDUCAŢIEI NAȚIONALE ŞI CERCETARII STIINTIFICE UNIVERSITATEA DE VEST DIN TIMIȘOARA.I CENTRUL DE DEZVOLTARE ACADEMICĂ. FIȘA DISCIPLINEI 1.
FIȘA DISCIPLINEI 1. Date despre program 1.1. Instituția de învățământ superior Universitatea de Vest din Timișoara 1.2. Facultatea Matematică și Informatică 1.3. Departamentul Informatică 1.4. Domeniul
Elemente de aritmetica
Elemente de aritmetică Anul II Februarie 2017 Divizibilitate în Z Definiţie Fie a, b Z. Spunem că a divide b (scriem a b) dacă există c Z astfel încât b = ac. In acest caz spunem că a este un divizor al
PROIECT DIDACTIC
Plan de lecție Informații generale Obiectul: Matematică Clasa: a VII - a Durata: 50 min Mijloace TIC: calculatorul profesorului cu videoproiector,calculatoare pentru elevi Tema lecției: Aria triunghiului
MergedFile
PROIECT DIDACTIC Clasa a VII-a Matematică Proiect didactic realizat de profesor Tatiana Predoană, Fundația Noi Orizonturi, în cadrul programului - pilot Digitaliada, revizuit de Monica Popovici, profesor
Microsoft Word - a5+s1-5.doc
Unitatea şcolară: Şcoala cu cls. I-VIII Sf. Vineri Profesor: Gh. CRACIUN Disciplina: Matematică Clasa a V-a / 4 ore pe săpt./ Anul şcolar 007-008 PROIECTAREA DIDACTICĂ ANUALĂ Număr săptămâni: 35 Număr
Limbaje Formale, Automate si Compilatoare
Limbaje Formale, Automate şi Compilatoare Curs 1 2018-19 LFAC (2018-19) Curs 1 1 / 45 Prezentare curs Limbaje Formale, Automate şi Compilatoare - Curs 1 1 Prezentare curs 2 Limbaje formale 3 Mecanisme
Microsoft Word - 12 Emilia PAUSAN.doc
CONFERINȚA NAȚIONALĂ DE INSTRUMENTAȚIE VIRTUALĂ, EDIȚIA A V-A, BUCURE TI, MAI 2008 53 Experimente simple cu achiziție de semnal Profesor Emilia Păuşan, Liceul Teoretic Tudor Vladimirescu, Bucureşti Abstract
VALORIFICAREA EXPERIENŢEI POZITIVE PRIVIND PROIECTAREA CURRICULARĂ ÎN ÎNVĂŢĂMÂNTUL LICEAL PORNIND DE LA COMPETENŢE CA FINALITĂŢI ALE ÎNVĂŢĂRII Prof. P
VALORIFICAREA EXPERIENŢEI POZITIVE PRIVIND PROIECTAREA CURRICULARĂ ÎN ÎNVĂŢĂMÂNTUL LICEAL PORNIND DE LA COMPETENŢE CA FINALITĂŢI ALE ÎNVĂŢĂRII Prof. Popa Daniela Livia Liceul Tehnologic Sfântul Pantelimon,
Probleme date la examenul de logică matematică şi computaţională. Partea a II-a Claudia MUREŞAN Universitatea din Bucureşti Facultatea de Matematică ş
Probleme date la examenul de logică matematică şi computaţională. Partea a II-a Claudia MUREŞAN Universitatea din Bucureşti Facultatea de Matematică şi Informatică Academiei 4, RO 0004, Bucureşti, România
Investeşte în oameni
FIŞA DISCIPLINEI 1 1. Date despre program 1.1 Instituţia de învăţământ superior Universitatea Politehnică Timișoara 1. Facultatea / Departamentul 3 Facultatea de Inginerie Hunedoara / Inginerie Electrică
MINISTERUL EDUCAŢIEI AL REPUBLICII MOLDOVA UNIVERSITATEA DE STAT ALECU RUSSO DIN BĂLŢI FACULTATEA DE ȘTIINȚE REALE, ECONOMICE ȘI ALE MEDIULUI CATEDRA
MINISTERUL EDUCAŢIEI AL REPUBLICII MOLDOVA UNIVERSITATEA DE STAT ALECU RUSSO DIN BĂLŢI FACULTATEA DE ȘTIINȚE REALE, ECONOMICE ȘI ALE MEDIULUI CATEDRA DE MATEMATICĂ ȘI INFORMATICĂ Curriculum Grafica computațională
14. Analiza computationala - MA 2
FIȘA DISCIPLINEI 1. Date despre program 1.1. Instituția de învățământ superior Universitatea de Vest din Timișoara 1.2. Facultatea Matematică și Informatică 1.3. Departamentul Matematică 1.4. Domeniul
O teoremă de reprezentare (II) Marian TETIVA 1 Abstract. In this paper some (in general well-known) results on complete sequences are exposed, with ap
O teoremă de reprezentare (II) Marian TETIVA 1 Abstract. In this paper some (in general well-known) results on complete sequences are exposed, with applications to Erdős-Suranyi sequences. We start from
Copyright c 2001 ONG TCV Scoala Virtuala a Tanarului Matematician 1 Ministerul Educatiei si Stiintei Examenul de bacalaureat la
Copyright c 1 ONG TCV Scoala Virtuala a Tanarului Matematician http://math.ournet.md 1 Ministerul Educatiei si Stiintei Examenul de bacalaureat la matematica, Profilurile: fizica-matematica, economie,
Coordonate baricentrice Considerăm în plan un triunghi ABC şi un punct Q în interiorul său, fixat arbitrar. Notăm σ c = aria ( QAB) σ a = aria ( QBC),
Coordonate baricentrice Considerăm în plan un triunghi ABC şi un punct Q în interiorul său, fixat arbitrar Notăm σ c = aria ( QAB) = aria ( QBC), = aria ( QCA) şi σ = aria ( ABC), astfel încât σ = + +
Lecții de pregă,re la informa,că Admitere 2019 Tema: Discutarea problemelor date la ul,mele sesiuni de admitere Bogdan Alexe
Lecții de pregă,re la informa,că Admitere 2019 Tema: Discutarea problemelor date la ul,mele sesiuni de admitere Bogdan Alexe bogdan.alexe@fmi.unibuc.ro Cuprinsul lecției de azi Enunțuri și rezolvări pentru
Introducere în statistică
Tudor Călinici 2015 Diferenţierea dintre aplicaţiile descriptive şi aplicaţiile de tip inferenţial Familiarizarea cu terminologia specifică statisticii Variabila Populație statistică Eșantion Talie Bias
Curs 3 Permutari cu repetitie. Combinari. Algoritmi de ordonare si generare
Curs 3 Permutări cu repetiţie. Combinări. Algoritmi de ordonare şi generare Octombrie 2015 Cuprins Algoritmi de ordonare şi generare pentru permutări cu repetiţie Reprezentarea binară a submulţimilor Algoritmi
Slide 1
Gruparea (si clasificarea) fuzzy a datelor Introducere Aspecte teoretice generale Gruparea tranșantă Metode fuzzy FCM SC Utilizarea metodelor fuzzy în matlab. Exemplificare Introducere (1) Obiectivul grupării
FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituţia de învăţământ superior Universitatea Babeş-Bolyai Cluj-Napoca 1.2 Facultatea Facultatea de Mate
FIŞA DISCIPLINEI 1. Date despre program 1.1 Instituţia de învăţământ superior Universitatea Babeş-Bolyai Cluj-Napoca 1.2 Facultatea Facultatea de Matematică şi Informatică 1.3 Departamentul Informatică
PROGRAMA ANALITICĂ PENTRU CLASA A X-A, CURSURI DE EXCELENŢĂ ANUL ŞCOLAR Studiul fizicii în clasele de excelenţă are ca finalitate încheierea
PROGRAMA ANALITICĂ PENTRU CLASA A X-A, CURSURI DE EXCELENŢĂ ANUL ŞCOLAR 2015-2016 Studiul fizicii în clasele de excelenţă are ca finalitate încheierea dezvoltării la elevi a unui set specific de competenţe-cheie